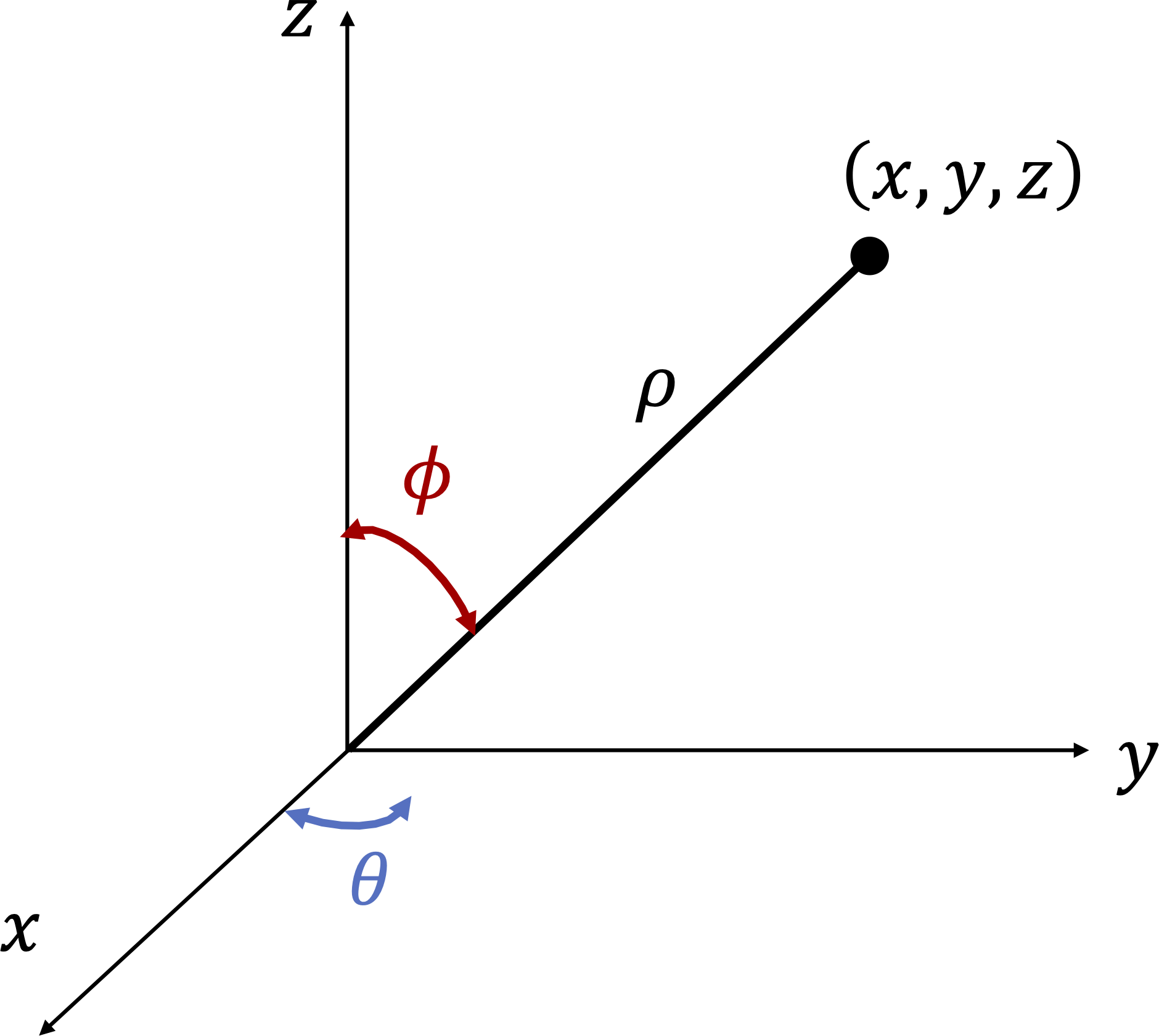Skip to main content\(\newcommand{\R}{\mathbb R}
\newcommand{\T}{\mathsf{T}}
\newcommand{\qed}{\scriptsize{\blacksquare}}
\newcommand{\hi}{\hat{\mathbf{i}}}
\newcommand{\hj}{\hat{\mathbf{j}}}
\newcommand{\hk}{\hat{\mathbf{k}}}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 2.4 Spherical Coordinates
The spherical coordinates \(\left(\rho, \theta , \phi \right)\) of a point \(\left(x,y,z\right)\) are defined as follows:
-
From cartesian to spherical.
\begin{equation*}
\rho = \sqrt{x^2+y^2+z^2}, \hspace{.5cm} \theta = \tan^{-1} \left(\displaystyle \frac{y}{x} \right), \hspace{0.5cm} \text{ and } \hspace{0.5cm} \phi = \cos^{-1} \left(\displaystyle \frac{z}{\sqrt{x^2+y^2+z^2}}\right)
\end{equation*}
We follow the same conditions on \(\theta\) as with the cylindrical coordinates.
-
From spherical to cartesian.
\begin{equation*}
x = \rho \sin \phi \cos \theta, \hspace{0.5cm} y = \rho \sin \phi \sin \theta, \hspace{0.5cm} \text{ and } \hspace{0.5cm} z= \rho \cos \phi.
\end{equation*}
where
\begin{equation*}
\rho \ge 0, \hspace{1cm} 0 \le \theta \le 2\pi, \hspace{1cm} 0 \le \phi \le \pi.
\end{equation*}
\(~\)
Checkpoint 2.4.1. From spherical to cylindrical coordinates.
What are the cylindrical coordinates of the point whose spherical coordinates are
\((2 ,\ 5 ,\ \frac{4 \pi}{6} )\) ?
\(r\) =
\(\theta\) =
\(z\)=
Checkpoint 2.4.2. From cartesian to spherical.
What are the spherical coordinates of the point whose rectangular coordinates are
\((3 ,\ 3 ,\ -3 )\) ?
\(\rho\) =
\(\theta\) =
\(\phi\) =