Skip to main content

Section 3.2 Equation of a Plane

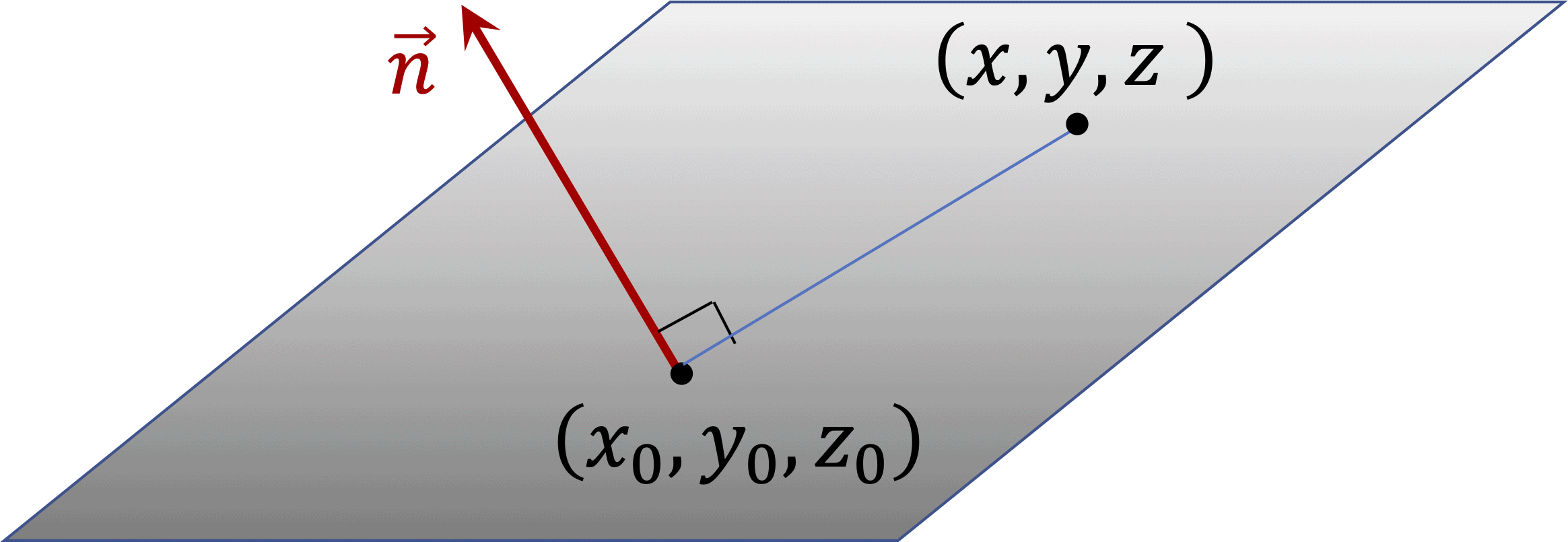
Definition 3.2.1. Scalar equation of a plane.

A plane containing a points \(P = (x_0, y_0, z_0)\) and with normal vector \(\vec{n} = \left[ a,b,c\right]^{\T}\text{,}\) satisfies the equation
\begin{equation*} \begin{array}{lcl} \vec{n} \cdot \vec{PQ} \amp = \amp 0,\\ \end{array} \end{equation*}
where \(Q= (x,y,z)\) is some generic point in the plane.
This gives the scalar equation of the plane,
\begin{equation*} \begin{array}{ccl} \vec{n}\cdot \vec{PQ} \amp = \amp 0,\\ \left[\begin{array}{c}a\\b\\c \end{array}\right] \cdot \left[\begin{array}{c}x-x_0\\y-y_0\\z-z_0 \end{array}\right] \amp = \amp 0,\\ a \left(x-x_0\right) + b \left(y-y_0\right) + c \left(z-z_0\right) \amp = \amp 0,\\ \end{array} \end{equation*}
Write an equation for the plane containing points \(P = \left(-1, 3, 1\right)\text{,}\) \(Q = \left(0, 2, -1\right)\) and \(R = \left(1, 4, 0\right.)\)
Solution: to write the equation of the plane we need the normal vector. A normal vector to a plane can be found as the cross product of two vector in the plane. In our example, those two vectors are,
\begin{equation*} \begin{array}{ccc} \vec{u} = \vec{PQ} \amp = \amp \left[\begin{array}{c} 1\\ -1\\ -2\end{array}\right],\\ \amp \amp \\ \vec{v} = \vec{PR} \amp = \amp \left[\begin{array}{c}2\\1\\-1 \end{array}\right]. \end{array} \end{equation*}
A normal vector will be then found as,
\begin{equation*} \begin{array}{ccc} \vec{u} \times \vec{v} \amp =\amp \left| \begin{array}{ccc} \hi \amp \hj \amp \hk\\ 1 \amp -1 \amp -2\\ 2 \amp 1\amp -1 \end{array}\right| \\ \amp = \amp \hi \left| \begin{array}{cc} -1 \amp -2\\ 1\amp -1 \end{array}\right| - \hj \left| \begin{array}{cc} 1 \amp -2\\ 2 \amp -1 \end{array}\right|+ \hk \left| \begin{array}{cc} 1 \amp -1 \\ 2 \amp 1 \end{array}\right|\\ \amp = \amp 3 \hi -3 \hj +3 \hk. \end{array} \end{equation*}
The equation of the plane is then,
\begin{equation*} \begin{array}{ccc} \vec{n} \cdot \vec{PX} \amp = \amp 0,\\ \left[\begin{array}{c} 3\\-3\\3\end{array} \right] \cdot \left[\begin{array}{c} x+1\\y-3\\z-1\end{array} \right] \amp =\amp 0\\ 3(x+1) - 3(y-3) + 3(z-1) \amp = \amp 0. \end{array} \end{equation*}
Parameterize the plane that contains the three points \((4, -3, 4)\text{,}\) \((4, -4, 10)\text{,}\) and \((20, 0, 45)\text{.}\)
\(\vec r(s,t) =\)
(Use \(s\) and \(t\) for the parameters in your parameterization, and enter your vector as a single vector, with angle brackets: e.g., as \lt 1 + s + t, s - t, 3 - t \gt.)
Answer.
\(\left<4+16t,3t-\left(3+s\right),4+6s+41t\right>\)
Solution.
\(P=(4, -3, 4)\text{,}\) \(Q=(4, -4, 10)\text{,}\) and \(R=(20, 0, 45)\) are the displacement vectors
\begin{equation*} \vec v_1 =\vec{PQ} = \left\lt 0,-1,6\right> \end{equation*}
and
\begin{equation*} \vec v_2 = \vec{PR} = \left\lt 16,3,41\right>. \end{equation*}
Letting \(\vec r_0 = \left\lt 4,-3,4\right>\text{,}\) we have the parameterization
\begin{equation*} \vec r(s, t) = \vec r_0 + s\vec v_1+t\vec v_2 = \left\lt 4+16t,3t-\left(3+s\right),4+6s+41t\right>. \end{equation*}

Subsection 3.2.1 Vector Equation of a Plane

Definition 3.2.4. Linear combination of vectors.

A vector \(\vec{w}\) is called a linear combination of the vectors \(\vec{u}\) and \(\vec{v}\text{,}\) if it can be decomposed as
\begin{equation*} \vec{w} = a\vec{u} + b \vec{v}, \end{equation*}
for some scalars \(a\) and \(b\text{.}\)
Given two non-colinear vectors in a plane, any arbitrary vector, also in the plane, can be written as a linear combination of those two vectors, as shown in the movie below.
\(~\)
Let \(P_0 = (x_0, y_0, z_0)\) be a fixed point in the plane, and \(P = (x,y,z) \) be other arbritary point in the plane. The coordinates of \(P\) can be determined as
\begin{equation*} \vec{OP} = \vec{OP_0} + \vec{P_0P}, \end{equation*}
where \(\vec{P_0P}\) is the vector between the two points, and \(\vec{OP}\text{,}\) \(\vec{OP_0}\text{,}\) are the position vectors for the points \(P\) and \(P_0\text{,}\) respectively.
\(~\)
We can express \(\vec{P_0P}\) as a linear combination of two known (non-collinear) vectors in the plane, \(\vec{u}\) and \(\vec{v}\text{,}\)
\begin{equation*} \vec{P_0P} = a\, \vec{u} + b\,\vec{v}. \end{equation*}
So that,
\begin{equation*} \vec{OP} = \vec{OP_0} + \vec{P_0P} = \vec{OP_0} + a\, \vec{u} + b\,\vec{v}. \end{equation*}

Definition 3.2.5. Vector equation of a plane.

The vector equation of a plane,
\begin{equation*} \vec{r} = \vec{r}_0 + s \vec{u} + t \vec{v}, \hspace{0.5cm} s,t \in \R, \end{equation*}
gives the position vector \(\vec{r}\) of any point \((x,y,z)\) in the plane as the sum of the position vector \(\vec{r}_0\) of a fixed point \((x_0,y_0,z_0)\) in the plane and a linear combination of any two non-collinear vectors, \(\vec{u}\) and \(\vec{v}\text{,}\) that lie in the plane.

Definition 3.2.6. Parametric equations of a plane.

From the vector equation of a plane,
\begin{equation*} \begin{array}{ccc} \vec{r} \amp = \amp \vec{r}_0 + s \vec{u} + t \vec{v}\\ \left[\begin{array}{c}x\\y\\z \end{array} \right] \amp =\amp \left[\begin{array}{c} x_0\\y_0\\z_0 \end{array} \right] + s\, \left[\begin{array}{c}u_1\\u_2\\u_3 \end{array} \right] + t\, \left[\begin{array}{c}v_1 \\v_2\\v_3 \end{array} \right], \end{array} \end{equation*}
we obtain the parametric equations,
\begin{equation*} \begin{array}{ccc} x(s,t) \amp = \amp x_0 + s u_1 + t v_1\\ y(s,t) \amp =\amp y_0 + s u_2 + t v_2\\ z(s,t) \amp = \amp z_0 + s u_3 + t v_3\\ \end{array} \end{equation*}
for \(s,t \in \R\text{.}\)
Assume the following three points lie in a plane,
\begin{equation*} P_1 (3,0,-1), \hspace{0.5cm} P_2(4,7,-1), \hspace{0.5cm} \text{ and } \hspace{0.5cm} P_3(-3,1,2). \end{equation*}
Find the vector and parametric equations of the plane.
Solution.
We need one fixed point and two non-collinear vectors. Let
\begin{equation*} \begin{array}{ccc} \vec{u} = \vec{P_2P_1} \amp = \amp \left[ \begin{array}{c} 4-3\\ 7-0\\ -1-(-1) \end{array}\right]\\ \amp =\amp \left[ \begin{array}{c} 1\\ 7\\ 0 \end{array}\right], \amp \amp \\ \vec{v} = \vec{P_3P_2} \amp = \amp \left[ \begin{array}{c} -3-4\\ 1-7\\ 2-(-1) \end{array}\right]\\ \amp = \amp \left[ \begin{array}{c} -7\\ -6\\ 3 \end{array}\right]. \end{array} \end{equation*}
We note that \(\vec{u}\) and \(\vec{v}\) are non-collinear, since we cannot find one of them as a scalar multiple of the other.
And for the fixed point we have \(\vec{r}_0=\vec{OP_1}=\left[ \begin{array}{c}3\\0\\-1 \end{array}\right]\text{.}\)
With these, the vector equation for the plane is,
\begin{equation*} \vec{r} = \left[ \begin{array}{c} 3\\0\\-1 \end{array}\right] + s\left[ \begin{array}{c} 1\\ 7\\ 0 \end{array}\right] + t \left[ \begin{array}{c} -7\\ -6\\ 3 \end{array}\right]. \end{equation*}
The parametric equations are
\begin{equation*} \begin{array}{ccc} x(s,t) \amp = \amp 3 +s -7t\\ y(s,t) \amp =\amp 7s - 6t\\ z(s,t) \amp = \amp -1 + 3t. \end{array} \end{equation*}
Parameterize the plane that contains the three points \((5, 4, -3)\text{,}\) \((-8, 5, 8)\text{,}\) and \((55, 40, 15)\text{.}\)
\(\vec r(s,t) =\)
(Use \(s\) and \(t\) for the parameters in your parameterization, and enter your vector as a single vector, with angle brackets: e.g., as \lt 1 + s + t, s - t, 3 - t \gt.)
Answer.
\(\left<5-13s+50t,4+s+36t,11s-3+18t\right>\)
Solution.
\(P=(5, 4, -3)\text{,}\) \(Q=(-8, 5, 8)\text{,}\) and \(R=(55, 40, 15)\) are the displacement vectors
\begin{equation*} \vec v_1 =\vec{PQ} = \left\lt -13,1,11\right> \end{equation*}
and
\begin{equation*} \vec v_2 = \vec{PR} = \left\lt 50,36,18\right>. \end{equation*}
Letting \(\vec r_0 = \left\lt 5,4,-3\right>\text{,}\) we have the parameterization
\begin{equation*} \vec r(s, t) = \vec r_0 + s\vec v_1+t\vec v_2 = \left\lt 5-13s+50t,4+s+36t,11s-3+18t\right>. \end{equation*}
<Prev^TopNext>