Vector Projections

Section 1.6 Vector Projections

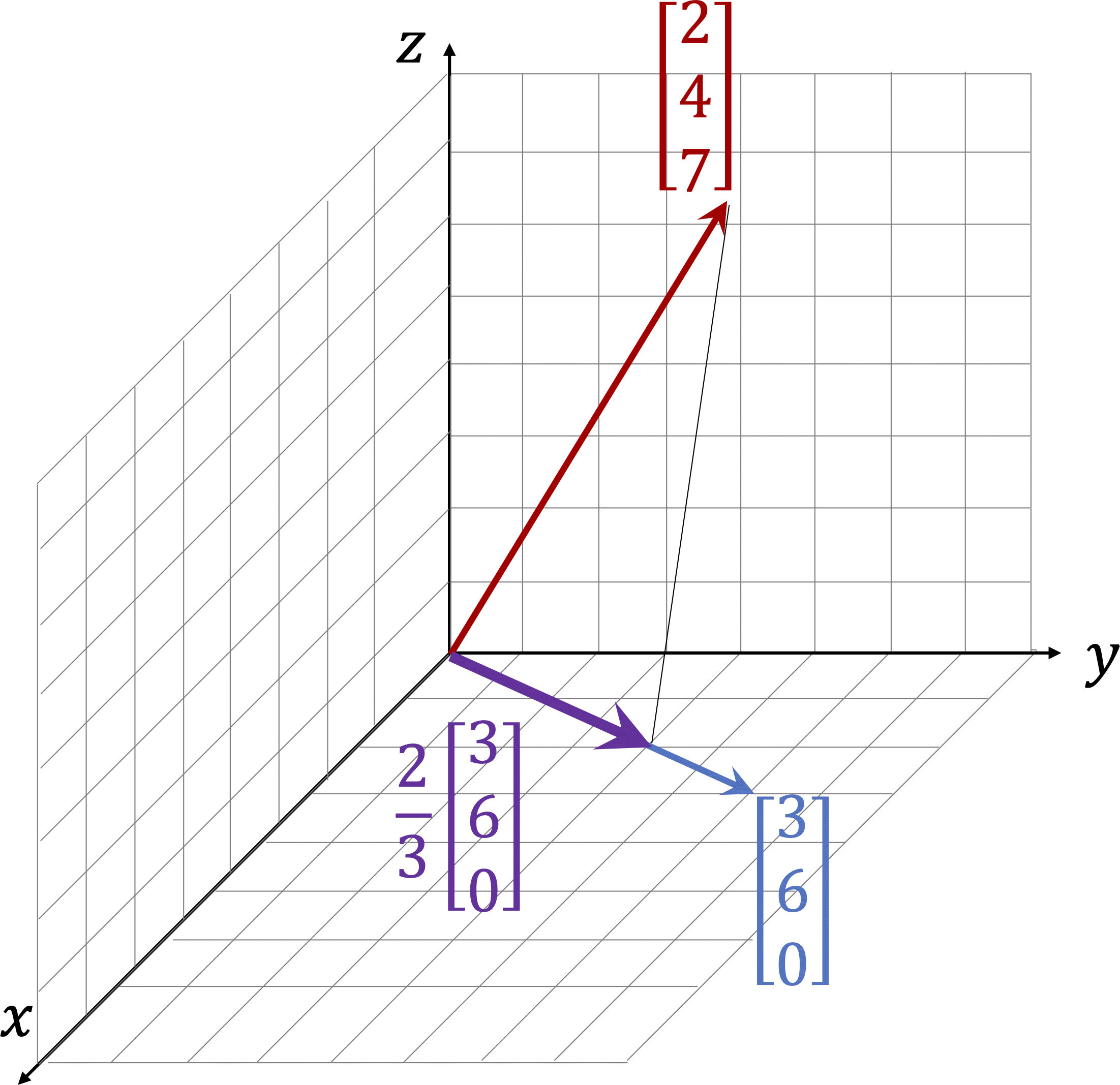
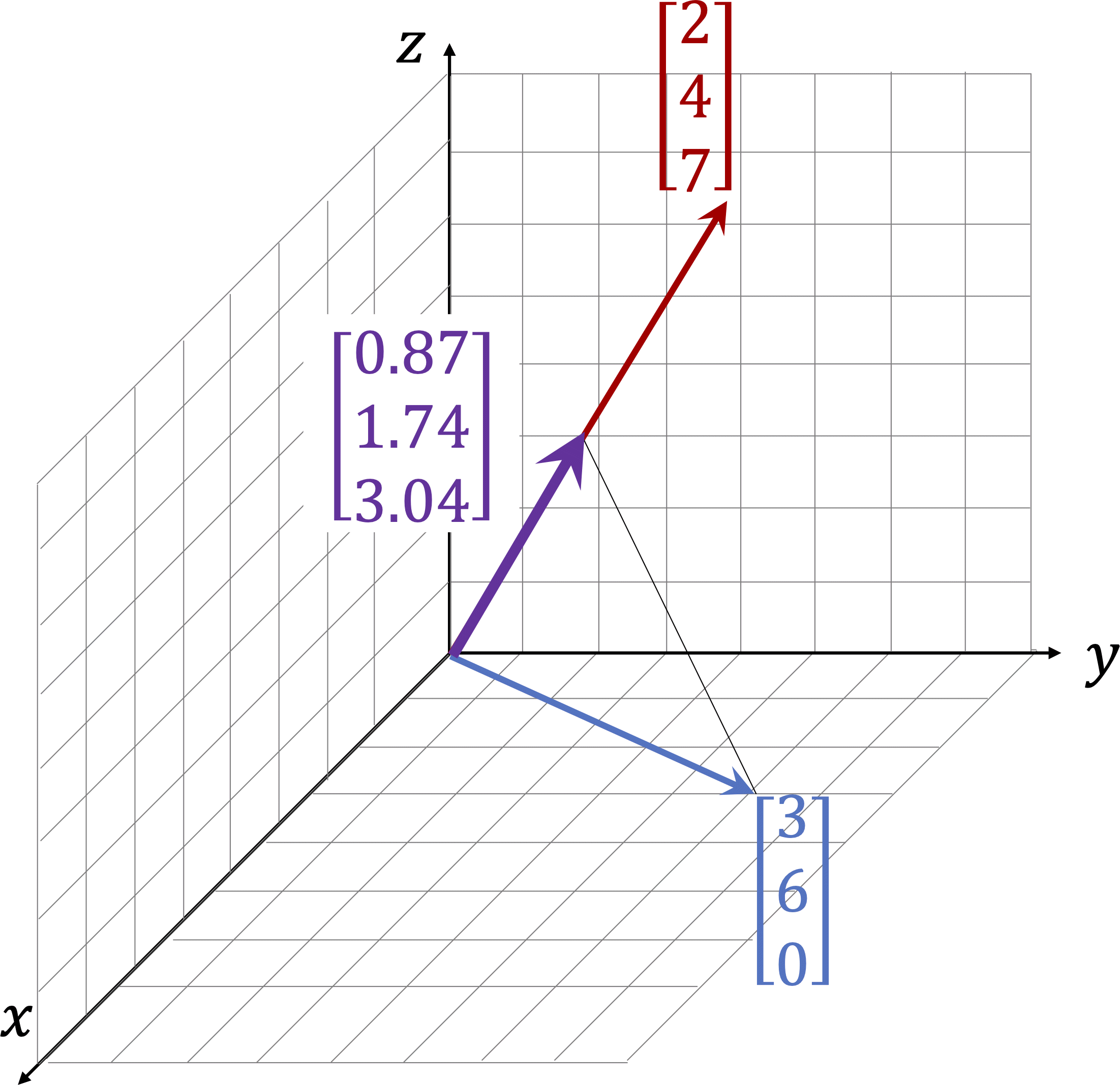
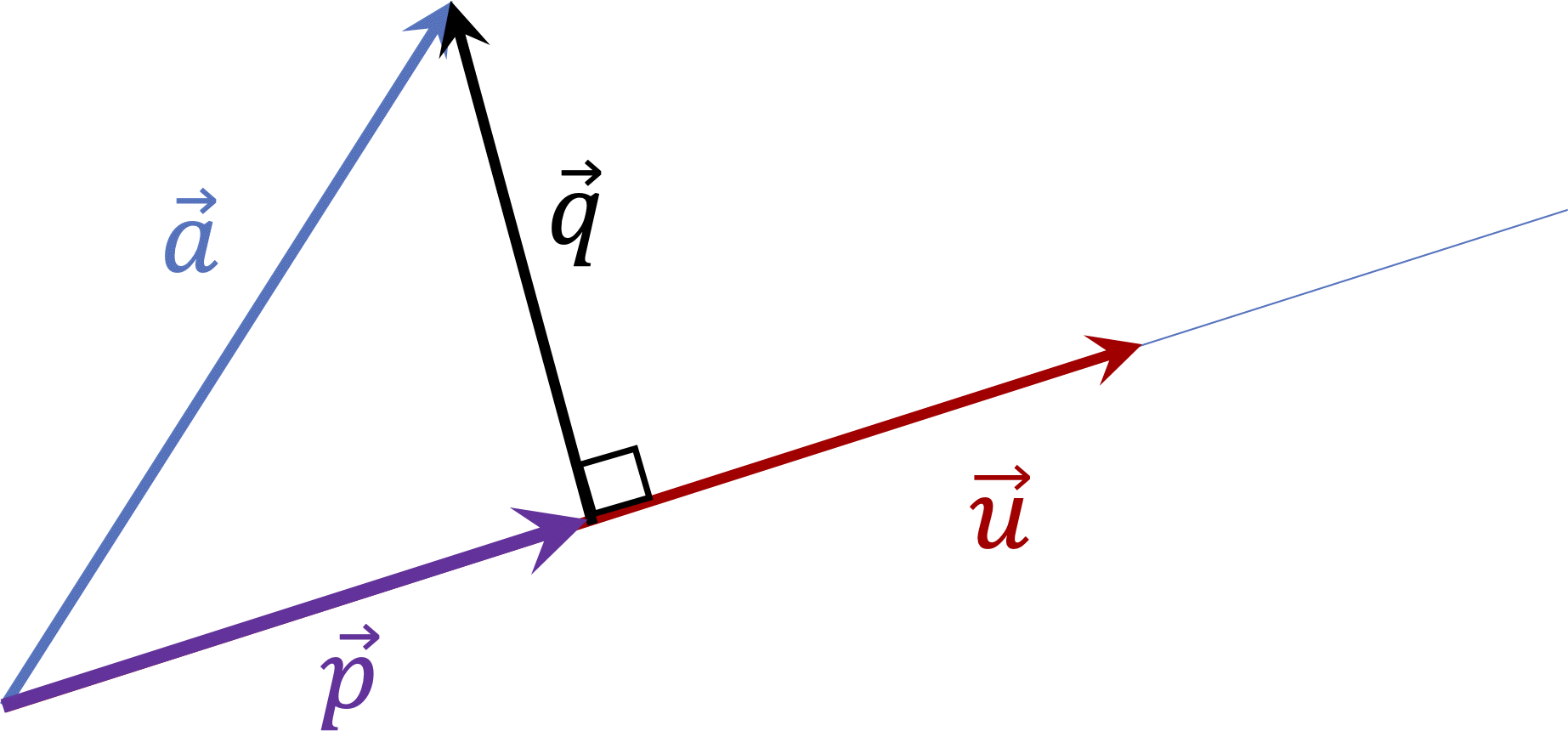
Definition 1.6.1. Projection along a vector.

Given two vectors \(\vec{a}\) and \(\vec{u}\text{,}\) the projection of \(\vec{a}\) along \(\vec{u}\) is given by \(\boldsymbol{\alpha \, \vec{u}}\) where

\begin{equation*} \alpha = \frac{\vec{a} \cdot \vec{u}}{\vec{u} \cdot \vec{u}}. \end{equation*}

Similarly, the projection of \(\vec{u}\) along \(\vec{a}\) is given by \(\boldsymbol{\beta \, \vec{a}}\) where

\begin{equation*} \beta = \frac{\vec{a} \cdot \vec{u}}{\vec{a} \cdot \vec{a}}. \end{equation*}

Example 1.6.2. Projection of a vector along another vector.

Find the projection of \(\vec{u} =\left[\begin{array}{c}2\\4\\7 \end{array}\right]\) along \(\vec{v} =\left[\begin{array}{c}3\\6\\0\end{array}\right].\)

\begin{equation*} \begin{array}{ccc} \vec{u} \cdot \vec{v} \amp = \amp 6+24 +0 = 30,\\ \vec{v} \cdot \vec{v} \amp = \amp 9+36 +0 = 45,\\ \alpha \amp =\amp \displaystyle\frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}} = \displaystyle \frac{30}{45} = \frac{2}{3}. \end{array} \end{equation*}

The projection is

\begin{equation*} \alpha \vec{v} = \displaystyle \frac{2}{3} \left[\begin{array}{c}3\\6\\0\end{array}\right] = \left[\begin{array}{c}2\\4\\0\end{array}\right]. \end{equation*}

\(~\)

Now find the projection of \(\vec{v}\) along \(\vec{u}\text{.}\)

\begin{equation*} \begin{array}{ccc} \beta \vec{u} \amp =\amp \left(\displaystyle \frac{\vec{u} \cdot \vec{v}} {\vec{u} \cdot \vec{u}}\right) \, \vec{u}\\ \amp = \amp \left(\displaystyle \frac{30}{4+16+49} \right)\, \left[\begin{array}{c}2\\4\\7\end{array}\right]\\ \amp = \amp \displaystyle \frac{30}{69} \, \left[\begin{array}{c}2\\4\\7\end{array}\right]= \displaystyle \frac{10}{23} \, \left[\begin{array}{c}2\\4\\7\end{array}\right]\\ \amp = \amp \left[\begin{array}{c}0.8696\\1.7391\\3.0435\end{array}\right]. \end{array} \end{equation*}

\(~\)

Definition 1.6.3. Scalar projection.

Given two vectors \(\vec{a}\) and \(\vec{u}\text{,}\) the scalar projection of \(\vec{a}\) onto \(\vec{u}\) is given by

\begin{equation*} s_{\vec{u}} \left(\vec{a}\right) = \frac{\vec{a} \cdot \vec{u}}{\Vert \vec{u} \Vert } = \frac{\vec{a} \cdot \vec{u}}{\sqrt{\vec{u} \cdot \vec{u}}}. \end{equation*}

Definition 1.6.4. Orthogonal Projection.

The orthogonal projection of \(\vec{a}\) onto \(\vec{u}\) is the vector.

\begin{equation*} \vec{p} = \text{Proj}_{\,\vec{u}}\left(\vec{a}\right) = \displaystyle \frac{\vec{a}\cdot \vec{u}} {\vec{u}\cdot \vec{u}}\, \vec{u}. \end{equation*}

Example 1.6.5. Vector decomposition.

Decompose the vector \(\vec{a}\) into a component parallel to \(\vec{u}\) and a component orthogonal to \(\vec{u}\) when

\begin{equation*} \vec{a} = \left[ 2,1,-3 \right]^{\T}, \hspace{0.5cm} \text{ and } \hspace{0.5cm} \vec{u} = \left[ -1, 1, 1 \right]^{\T}. \end{equation*}

Parallel component.

The component parallel to \(\vec{u}\) is given by,

\begin{equation*} \begin{array}{ccc} \vec{p} = \text{Proj}_{\,\vec{u}}\left(\vec{a}\right) \amp =\amp \displaystyle \frac{\vec{a}\cdot \vec{u}} {\vec{u}\cdot \vec{u}}\, \vec{u}\\ \amp = \amp \displaystyle \frac{-2 +1 -3}{1 + 1 +1 }\, \left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right]\\ \amp = \amp \displaystyle -\frac{4}{3}\, \left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right].\\ \end{array} \end{equation*}
Orthogonal component.

From the figure in Definition 1.6.4 the vector \(\vec{a} \) can be found as the sum of the orthogonal component \(\vec{q}\) and the parallel component \(\vec{p}\text{,}\)

\begin{equation*} \vec{a} = \vec{p} + \vec{q} \hspace{0.1cm} \text{ and we can solve for } \vec{q} \text{ as }\Rightarrow \vec{q} = \vec{a} - \vec{p}. \end{equation*}

\begin{equation*} \begin{array}{ccc} \vec{q} \amp =\amp \vec{a} - \vec{p}\\ \amp = \amp \left[\begin{array}{c} 2\\1\\-3 \end{array}\right] \displaystyle -\frac{4}{3}\, \left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right].\\ \amp = \amp \displaystyle \frac{1}{3}\left[\begin{array}{c} 10 \\-1\\-13 \end{array}\right]. \end{array} \end{equation*}