Section 2.2 Polar Coordinates
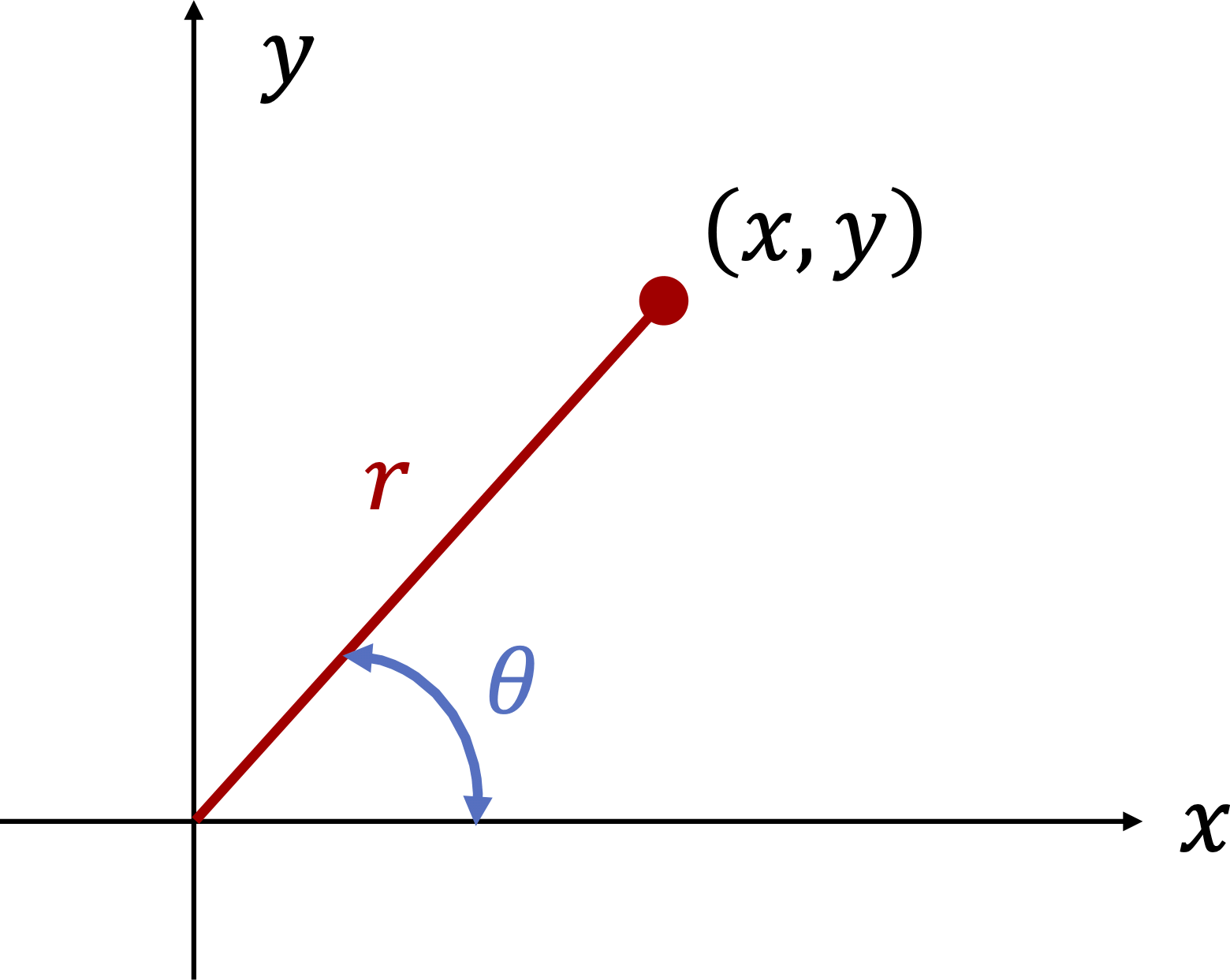
The standard way of representing point in \(\R^2\) is using rectangular coordinates, \(\left( x,y\right).\) However, sometimes is more convenient to instead use polar coordinates \(\left( r,\theta\right).\) The polar coordinates and the rectangular coordinates are related to each other by the following relations.
-
From cartesian to polar.\begin{equation*} r = \sqrt{x^2 + y^2}, \hspace{0.5cm} \text{ and } \hspace{0.5cm} \theta = \tan^{-1}\displaystyle\frac{y}{x}. \end{equation*}
-
From polar to cartesian.\begin{equation*} x = r \cos \theta, \hspace{0.5cm} \text{ and } \hspace{0.5cm} y = r \sin \theta. \end{equation*}
\(~\)
Find the distance between the two points: \(p_1 = \left(1, \displaystyle \frac{\pi}{6}\right)\) and \(p_2 = \left(3, \displaystyle -\frac{\pi}{2} \right)\)
The distance between two points in cartesian coordinates, \(\left(x_1,y_1\right)\) and \(\left(x_2,y_2\right)\text{,}\) is defined as
\begin{equation*}
\text{distance } = \sqrt{\left(x_1 - x_2\right)^2 + \left(y_1 - y_2\right)^2}.
\end{equation*}
To find the distance between two polar points, we first convert each point to cartesian coordinates and then apply the formula for distance.
\begin{equation*}
\begin{array}{ccl}
\left( x_1 , y_1\right) \amp =\amp \left(1 \cos \left(\displaystyle \frac{\pi}{6}\right),
1 \sin \left(\displaystyle \frac{\pi}{6}\right) \right)\\
\amp = \amp \left(\displaystyle \frac{\sqrt{3}}{2}, \displaystyle \frac{1}{2} \right).\\
\amp \amp \\
\left( x_2 , y_2\right) \amp =\amp \left(3 \cos \left(-\displaystyle\frac{\pi}{2}\right),
3 \sin \left(-\displaystyle \frac{\pi}{2}\right) \right)\\
\amp = \amp \left( 0,-3\right).\\
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccl}
\text{distance } \amp = \amp \sqrt{\left(\displaystyle \frac{\sqrt{3}}{2}-0 \right)^2 + \left(\displaystyle \frac{1}{2} - (-3)\right)^2}\\
\amp =\amp \sqrt{\displaystyle \frac{3}{4} + \displaystyle \frac{49}{4}} = \sqrt{\displaystyle \frac{52}{4}}\\
\amp =\amp \sqrt{13} \approx 3.61.
\end{array}
\end{equation*}
\(~\)
Checkpoint 2.2.2. From polar to cartesian.
For each set of polar coordinates \(\left(r,\theta \right)\text{,}\) match the equivalent cartesian coordinates \(\left(x,y\right)\text{.}\)
- \(~ \left( {2}, {-0.8} \pi \right)\)
- \(~ \left( {5}, {-0.7} \pi \right)\)
- \(~ \left( {5}, {-0.3} \pi \right)\)
- \(~ \left( {3}, {0.2} \pi \right)\)
\begin{equation*}
\begin{array}{cl}
\text{A} \hspace{0.2cm} \amp \left({2.93893},{-4.04508} \right)\\
\text{B} \hspace{0.2cm} \amp \left({-2.93893},{-4.04508} \right)\\
\text{C} \hspace{0.2cm} \amp \left({-1.61803},{-1.17557} \right)\\
\text{D} \hspace{0.2cm} \amp \left({2.42705},{1.76336} \right)\\
\end{array}
\end{equation*}
\(~\)
Checkpoint 2.2.3. From cartesian to polar.
For each set of cartesian coordinates \(\left(x,y\right)\text{,}\) match the equivalent polar coordinates \(\left(r,\theta \right)\text{.}\)
- \(~ \left( {-0.809017}, {0.587785} \right)\)
- \(~ \left( {-0.951057}, {-0.309017} \right)\)
- \(~ \left( {0}, {-5} \right)\)
- \(~ \left( {1.23607}, {-3.80423} \right)\)
\begin{equation*}
\begin{array}{cl}
\text{A} \hspace{0.2cm} \amp \left({\text{A}},{0.6} \pi \right)\\
\text{B} \hspace{0.2cm} \amp \left({\text{B}},{0.8} \pi \right)\\
\text{C} \hspace{0.2cm} \amp \left({\text{C}},{-0.5} \pi\right)\\
\text{D} \hspace{0.2cm} \amp \left({\text{D}},{0.1} \pi\right)\\
\end{array}
\end{equation*}


