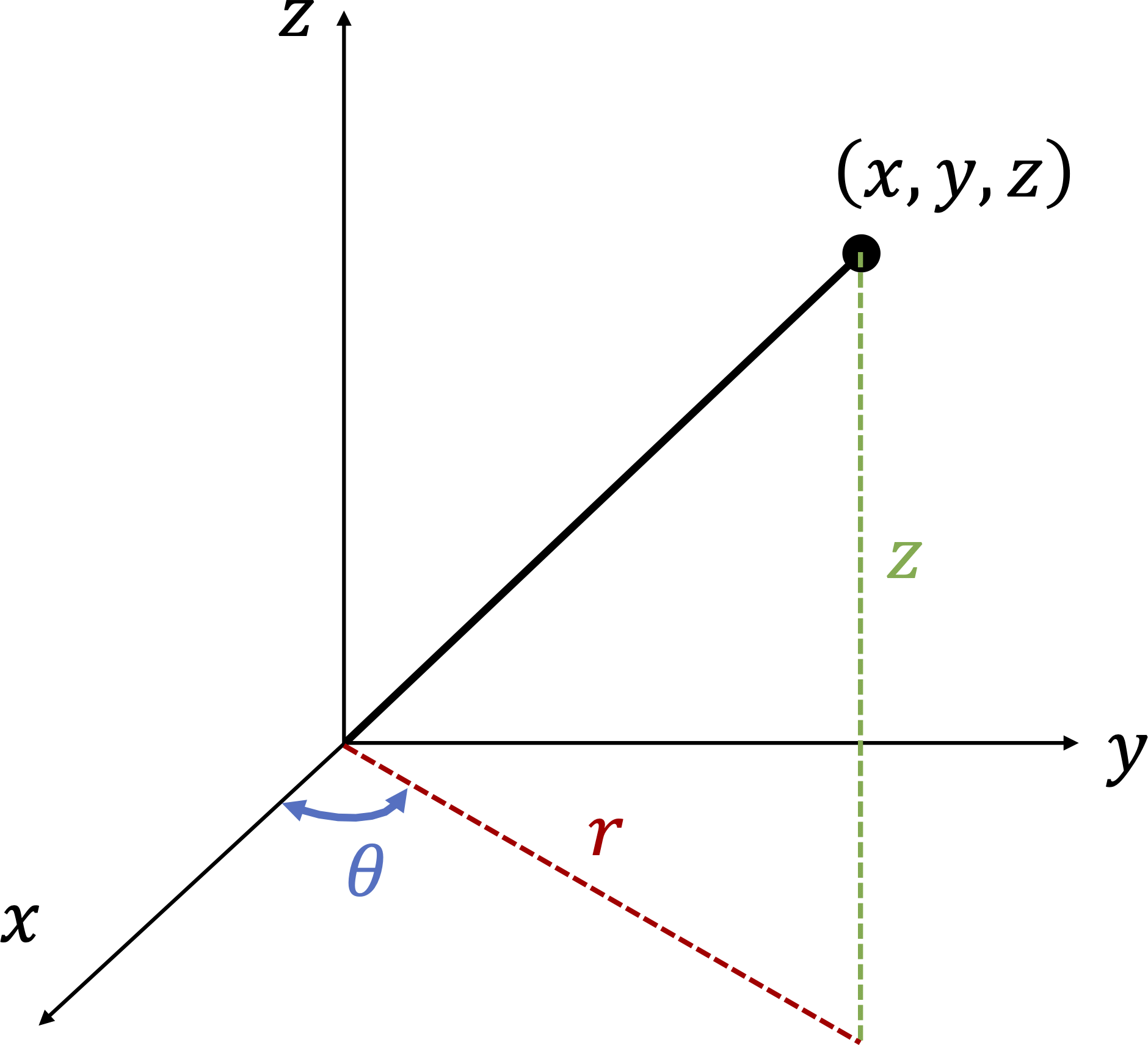
Cylindrical\(\left(r, \theta , z \right)\) and rectangular\(\left(x,y,z\right)\)coordinates are related to each other by the following relations.
From cartesian to cylindrical.
\begin{equation*}
r = \sqrt{x^2 + y^2}, \hspace{0.5cm} \text{ and } \hspace{0.5cm}
\theta = \left\{\begin{array}{ll}
\tan^{-1}\displaystyle\frac{y}{x} \amp \text{ if } x \gt 0 \text{ and } y \ge 0\\
\pi + \tan^{-1}\displaystyle\frac{y}{x} \amp \text{ if } x \lt 0\\
2 \pi + \tan^{-1}\displaystyle\frac{y}{x} \amp \text{ if } x \gt 0 \text{ and } y \lt 0\\
\end{array} \right.,
\hspace{0.5cm} \text{ and } \hspace{0.5cm} z = z.
\end{equation*}
The conditions on \(\theta\) is to ensure \(0 \le \theta \le 2 \pi\text{.}\)
\(~\)
From cylindrical to cartesian.
\begin{equation*}
x = r \cos \theta, \hspace{0.5cm} y = r \sin \theta, \hspace{0.5cm} \text{ and } \hspace{0.5cm} z=z.
\end{equation*}
