Skip to main content

Section 3.1 Equation of a line

Definition 3.1.1. Vector equation of a line.

The vector equation for the line through the point \(\left(a,b,c\right)\) and parallel to the vector \(\vec{v} \) is
\begin{equation*} \left[\begin{array}{c} x\\y\\z \end{array}\right] = \left[\begin{array}{c} a\\b\\c \end{array}\right] + t \vec{v}. \end{equation*}
Find the parametric equations of the line through the two points \((-2,1,5)\) and \((1,3,-2).\)
Soltuion: A vector passing through the two points is
\begin{equation*} \vec{v} = \left[\begin{array}{c} v_1\\v_2\\v_3 \end{array}\right] = \left[\begin{array}{c} 1-(-2)\\3-1\\-2-5 \end{array}\right] = \left[\begin{array}{c} 3\\2\\-7 \end{array}\right]. \end{equation*}
The vector equation of the line is given by,
\begin{equation*} \left[\begin{array}{c} x\\y\\z \end{array}\right] = \left[\begin{array}{c} 1\\3\\-2 \end{array}\right] + \left[\begin{array}{c} 3\\2\\-7 \end{array}\right] t. \end{equation*}
Equivalently the parametric equations are,
\begin{equation*} \begin{array}{ccl} x(t) \amp = \amp 1 + 3t\\ y(t) \amp =\amp 3 + 2t\\ z(t) \amp =\amp -2 - 7t. \end{array} \end{equation*}
Find the vector and parametric equations for the line through the point \(P=(1, -3, 1)\) and the point \(Q=(-1, -1, 5)\text{.}\)
Vector Form: \(\mathbf r = \langle\), , 1 \(\rangle + t \langle\) , , 4 \(\rangle\)
Parametric form (parameter \(t\text{,}\) and passing through \(P\) when \(t = 0\)):
\(x = x(t) =\)
\(y = y(t) =\)
\(z = z(t) =\)
Answer 1.
\(1\)
Answer 2.
\(-3\)
Answer 3.
\(-2\)
Answer 4.
\(2\)
Answer 5.
\(1+t\!\left(-2\right)\)
Answer 6.
\(-3+t\cdot 2\)
Answer 7.
\(1+t\cdot 4\)
\(\mathbf{r}_1(t) = \left(-13,16,-14\right) + t \left\lt -4,2,-1\right>\)
\(\mathbf{r}_2(t) = \left(-4,4.5,-6.5\right) + t \left\lt 2,1,-1\right>\)
Find the point of intersection, \(P\text{,}\) of the lines \(\mathbf{r}_1\) and \(\mathbf{r}_2\text{.}\)
\(P\) =
Answer.
\(\left(3,8,-10\right)\)
Solution.
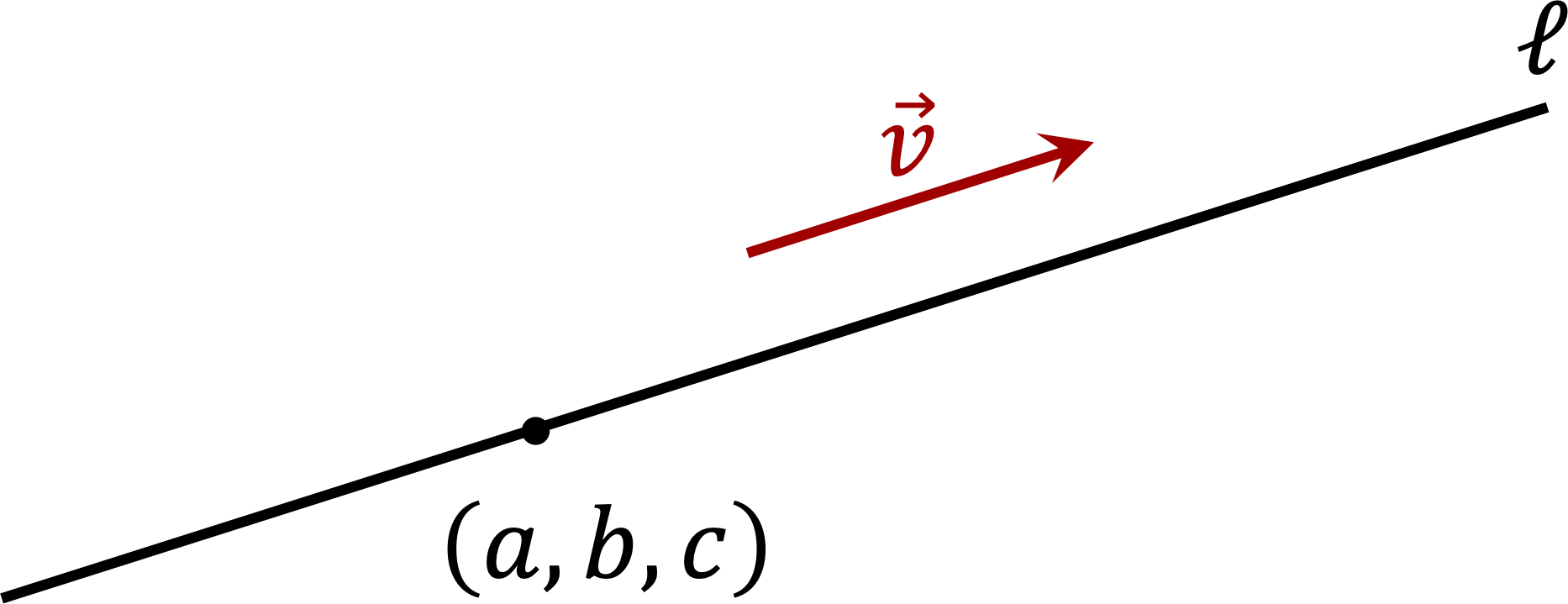
\(t_1\) and \(t_2\) such that \(\mathbf{r}_1(t_1) = \mathbf{r}_2(t_2)\text{.}\) That is \(\left\lt -13,16,-14\right> + t_1 \left\lt -4,2,-1\right> = \left\lt -4,4.5,-6.5\right> + t_2 \left\lt 2,1,-1\right>\text{.}\) This is equivalent to the three equations for the components: \(x = -13 - 4 t_1 = -4 + 2 t_2\text{,}\) \(y = 16 + 2 t_1 = 4.5 + 1 t_2\text{,}\) \(z = -14 - 1 t_1 = -6.5 - 1 t_2\text{.}\) Solving the first two equations for \(t_1\) and \(t_2\) in turn yields \(t_1 = -4\) and \(t_2 = 3.5\) Now, substituting these values into the third equation yields \(-14 - 4 * -1 = -6.5 + 3.5 * -1\) \(-10 = -10\) Since this does indeed come out equal, the lines intersect at the point \(\left\lt -13,16,-14\right> - 4 * \left\lt -4,2,-1\right> = \left\lt 3,8,-10\right>\) Note: If the third equation could not be reconciled, that would mean that the lines do not intersect.

Definition 3.1.5. Symmetric Equations of a Line.

Let \(\ell \) be the line with parametric equations,
\begin{equation*} x(t) = x_0 + at, \hspace{0.5cm} y(t) = y_0 + bt, \hspace{0.5cm} \text{ and } \hspace{0.5cm} z(t) = z_0 + ct. \end{equation*}
If \(a, b, c \ne 0\text{,}\) \(\ell\) can be described by the symmetric equations:
\begin{equation*} \displaystyle \frac{x-x_0}{a} = \displaystyle \frac{y-y_0}{b} = \displaystyle \frac{z-z_0}{c} \end{equation*}

Insight 3.1.6.

Note that if a line passes through the origin, it has symmetric equations,
\begin{equation*} \displaystyle \frac{x}{a} = \displaystyle \frac{y}{b} = \displaystyle \frac{z}{c} \end{equation*}
(a) Find a parametric equation for the line through the point \(\left(5,4,3\right)\) and in the direction of \(a\vec i +b\vec j+c\vec k\text{.}\)
\(\vec r(t) =\)
(b) Find conditions on \(a,b,c\) so that the line you found in part (a) goes through the origin. (Be sure you can give a reason for your answer.) Then use your work to give two distinct triples \(a,b,c\) that result in the line passing through the origin.
Choice 1: \(a =\) , \(b =\) , \(c =\) ;
Choice 2: \(a =\) , \(b =\) , \(c =\) .
Answer 1.
\(\left(5,4,3\right)+t\!\left(1.404\,\mathit{\vec i}+2.71828\,\mathit{\vec j}+1.1771\,\mathit{\vec k}\right)\)
Answer 2.
\(5\)
Answer 3.
\(4\)
Answer 4.
\(3\)
Answer 5.
\(-5\)
Answer 6.
\(-4\)
Answer 7.
\(-3\)
Solution.
(a) Parametric equations are
\begin{equation*} x = 5 + a t,\quad y = 4 + b t,\quad z = 3 + c t, \end{equation*}
or
\begin{equation*} \vec r(t) = (5 + a t)\,\vec i + (4 + b t)\,\vec j + (3 + c t)\,\vec k. \end{equation*}
(b) The line goes through the origin if the position vector \(5 \vec i + 4 \vec j + 3 \vec k\) is parallel to the vector \(a\vec i +b\vec j +c\vec k\text{.}\) This occurs if \(a,b,c\) are in the ratio \(5:4:3\text{;}\) that is if
\begin{equation*} \frac a{5} =\frac b {4} =\frac c{3}. \end{equation*}
Any values satisfying this are appropriate.
<Prev^TopNext>