Subsection 1.2 Matrix operations
Subsubsection 1.2.1 Matrix addition
Let \(\boldsymbol{A}_{m\times n} \) and \(\boldsymbol{B}_{m\times n} \) be two matrices of the same size. The sum \(\boldsymbol{C}_{m\times n} = \boldsymbol{A} + \boldsymbol{B} \) is obtained by adding the corresponding elements of \(\boldsymbol{A} \) and \(\boldsymbol{B}: \) \(c_{ij} = a_{ij} + b_{ij}. \) If \(\boldsymbol{A} \) and \(\boldsymbol{B} \) are not the same size the sum does not exist.
Let
\begin{equation*}
\boldsymbol{A} = \left[\begin{array}{cccc}
3 \amp -2 \amp 1 \amp 0\\
4 \amp 0 \amp 3 \amp -5\\
\end{array}\right], \hspace{2.5cm} \boldsymbol{B} = \left[\begin{array}{cccc}
0 \amp 7 \amp -2 \amp 1\\
1 \amp 4 \amp -1 \amp 3\\
\end{array}\right].
\end{equation*}
Find \(\boldsymbol{A}+\boldsymbol{B} \text{.}\)
\begin{equation*}
\boldsymbol{A} + \boldsymbol{B} = \left[\begin{array}{cccc}
3 \amp -2 \amp 1 \amp 0\\
4 \amp 0 \amp 3 \amp -5\\
\end{array}\right] \hspace{.5cm} + \hspace{.5cm} \left[\begin{array}{cccc}
0 \amp 7 \amp -2 \amp 1\\
1 \amp 4 \amp -1 \amp 3\\
\end{array}\right] \hspace{.5cm} = \hspace{.5cm}
\left[\begin{array}{cccc}
3 \amp 5 \amp -1 \amp 1\\
5 \amp 4 \amp 2 \amp 2\\
\end{array}\right].
\end{equation*}
Checkpoint 1.2.6. Determining if addition exists.
Consider the matrices \(\boldsymbol{A}_{{3}\times {4}}\text{,}\) \(\boldsymbol{B}_{{4}\times {3}}\text{,}\) \(\boldsymbol{C}_{{3}\times {4}}\text{,}\) and \(\boldsymbol{D}_{{6}\times {4}}\text{.}\)
Determine if the following operations exist
-
\(\boldsymbol{A} + \boldsymbol{B}\)
- Yes
- No
-
\(\boldsymbol{A} + \boldsymbol{C}\)
- Yes
- No
-
\(\boldsymbol{B} + \boldsymbol{C}\)
- Yes
- No
-
\(\boldsymbol{C} + \boldsymbol{D}\)
- Yes
- No
Checkpoint 1.2.7. Adding matrices.
Find \(\boldsymbol{A} + \boldsymbol{B}\) where
\begin{equation*}
\boldsymbol{A} = \begin{array}{lrrrr}
\lceil \amp{-1} \amp {4} \amp {-1} \amp \rceil \\
\lfloor \amp {-8} \amp {7} \amp {7} \amp \rfloor
\end{array}\hspace{1cm} \text{ and } \hspace{1cm}
\boldsymbol{B} = \begin{array}{ccc}
\lceil \amp{5} \amp {-8} \amp {-8} \amp \rceil \\
\lfloor \amp{9} \amp {-6} \amp {-6} \amp \rfloor
\end{array}.
\end{equation*}
| \(\,\) | \(\lceil\) | \(\rceil\) | |||
| \(\boldsymbol{A} + \boldsymbol{B} =\) | \(\lfloor\) | \(\rfloor\) | |||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
Answer 1.
Answer 2.
Answer 3.
Answer 4.
Answer 5.
Answer 6.
Solution.
\(4\)
\(-4\)
\(-9\)
\(1\)
\(1\)
\(1\)
\begin{equation*}
\boldsymbol{A} + \boldsymbol{B} =\left[ \begin{array}{ccc}
{-1}+ ({5}) \amp {4}+ ({-8}) \amp {-1}+ ({-8}) \\
{-8} + ({9}) \amp {7}+({-6}) \amp {7} + ({-6})
\end{array}\right] = \left[ \begin{array}{ccc}
{4} \amp {-4} \amp {-9} \\
{1} \amp {1} \amp {1}
\end{array}\right]
\end{equation*}
\(\,\)
Subsubsection 1.2.2 Matrix-scalar multiplication
Let \(\boldsymbol{A}_{m \times n} \) be a matrix and \(c\) a scalar. The scalar multiple of \(\boldsymbol{A}\) by \(c\text{,}\) denoted \(c\boldsymbol{A}\text{,}\) is the \(m \times n\) matrix obtained by multiplying every element of \(\boldsymbol{A}\) by \(c\text{,}\) \(\boldsymbol{B} = c\boldsymbol{A} \Rightarrow b_{ij} = c \cdot a_{ij}.\)
Example 1.2.8. Scalar multiplication.
Let
\begin{equation*}
\boldsymbol{A} = \left[\begin{array}{cccc}
4 \amp -1 \amp -1 \amp 3\\
1 \amp 2 \amp -4 \amp -5\\
\end{array}\right],
\end{equation*}
find \(3 \, \boldsymbol{A}.\)
\begin{equation*}
3 \, \boldsymbol{A} = \left[\begin{array}{cccc}
3 \cdot 4 \amp 3 \cdot (-1) \amp 3 \cdot (-1) \amp 3 \cdot 3\\
3 \cdot 1 \amp 3 \cdot 2 \amp 3 \cdot (-4) \amp 3 \cdot (-5)\\
\end{array}\right] = \left[\begin{array}{cccc}
12 \amp -3 \amp -3 \amp 9\\
3 \amp 6 \amp -12 \amp -15\\
\end{array}\right].
\end{equation*}
Checkpoint 1.2.9. Multiply a matrix by a scalar.
Find \({3} \boldsymbol{A}\) where
\begin{equation*}
\boldsymbol{A} = \begin{array}{lrrr}
\lceil \amp {1} \amp {-2} \amp\rceil \\
\vert \amp {7} \amp {6} \amp \vert \\
\lfloor \amp {6} \amp {-2} \amp \rfloor
\end{array}.
\end{equation*}
| \(\,\) | \(\lceil\) | \(\rceil\) | ||
| \(3 \boldsymbol{A} =\) | \(\vert\) | \(\vert\) | ||
| \(\,\) | \(\lfloor\) | \(\rfloor\) | ||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
Answer 1.
Answer 2.
Answer 3.
Answer 4.
Answer 5.
Answer 6.
Solution.
\(3\)
\(-6\)
\(21\)
\(18\)
\(18\)
\(-6\)
\begin{equation*}
{3}\boldsymbol{A} =\left[ \begin{array}{cc}
{3} ({1}) \amp {3} ({-2}) \\
{3} ({7}) \amp {3}({6}) \\
{3} ({6}) \amp {3} ({-2})
\end{array}\right] = \left[ \begin{array}{ccc}
{3} \amp {-6} \\
{21} \amp {18} \\
{18} \amp {-6}
\end{array}\right].
\end{equation*}
Checkpoint 1.2.10. Matrix subtraction.
Let
\begin{equation*}
\boldsymbol{A} = \left[ \begin{array}{cc}
{3} \amp {-9} \\
{-4} \amp {6}
\end{array}\right] \hspace{1cm} \text{and} \hspace{1cm}
\boldsymbol{B} = \left[ \begin{array}{cc}
{7} \amp {8} \\
{8} \amp {4}
\end{array}\right].
\end{equation*}
Find \(\boldsymbol{A} - \boldsymbol{B} \text{.}\)
This is accomplished by combining the addition and scalar multiplication operations introduced in this section.
Finding \(\boldsymbol{A} - \boldsymbol{B}\) is equivalent at finding \(\boldsymbol{A} + ((-1) \cdot \boldsymbol{B}).\) That is, we first multiply \(\boldsymbol{B}\) by \(-1\) and then add this new matrix to \(\boldsymbol{A}.\) Use this procedure to find \(\boldsymbol{A} - \boldsymbol{B} \text{.}\)
| \(\,\) | \(\lceil\) | \(\rceil\) | ||
| \(\boldsymbol{A} - \boldsymbol{B} =\) | \(\lfloor\) | \(\rfloor\) | ||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
Answer 1.
Answer 2.
Answer 3.
Answer 4.
Solution.
\(-4\)
\(-17\)
\(-12\)
\(2\)
\begin{equation*}
\boldsymbol{A} - \boldsymbol{B} =\left[ \begin{array}{cc}
{3} - ({7}) \amp {-9} - ({8})\\
{-4} - ({8}) \amp {6} - ({4})
\end{array}\right] = \left[ \begin{array}{ccc}
{-4} \amp {-17} \\
{-12} \amp {2}
\end{array}\right].
\end{equation*}
\(\,\)
Subsubsection 1.2.3 Matrix-matrix multiplication
The matrix product of the matrix \(\boldsymbol{A}_{m \times n} \) and the matrix \(\boldsymbol{B}_{n \times r}, \) is the matrix \(\boldsymbol{C}_{m \times r} = \boldsymbol{A}_{m \times n} \times \boldsymbol{B}_{n \times r},\) where
\begin{equation*}
c_{ij} = a_{i1}\, b_{1j} + a_{i2}\, b_{2j} + \cdots + a_{in}\, b_{nj}.
\end{equation*}
That is, the \(ij \) element of the product results from multiplying the \(i^{th}\) row of the first matrix with the \(j^{th}\) column of the second matrix and adding the entries.
\begin{equation*}
\boldsymbol{C}_{m \times r} = \boldsymbol{A}_{m \times n} \times \boldsymbol{B}_{n \times r} =
\left[ \begin{array}{cccc}
\amp \vdots \amp \amp \\
a_{i1} \amp a_{i2} \amp \cdots \amp a_{in}\\
\amp \vdots \amp \amp
\end{array}\right]\,
\left[ \begin{array}{ccc}
\amp b_{1j} \amp \\
\cdots\amp b_{2j} \amp \cdots \\
\amp \vdots \amp \\
\amp b_{nj} \amp
\end{array}\right] =
\left[ \begin{array}{ccc}
\amp \vdots\amp \\
\cdots\amp c_{ij} \amp \cdots \\
\amp \vdots \amp
\end{array}\right].
\end{equation*}
Example 1.2.11. Matrix multiplication.
Let \(\boldsymbol{A} \) and \(\boldsymbol{B} \) be the two matrices given below. Find \(\boldsymbol{C} = \boldsymbol{A} \times \boldsymbol{B}.\)
\begin{equation*}
\boldsymbol{A} = \left[ \begin{array}{cccc}
3 \amp -2 \amp 4 \amp 2 \\
1 \amp 3 \amp -5 \amp -2 \\
\end{array}\right],
\hspace{2cm}
\boldsymbol{B} = \left[ \begin{array}{ccc}
0 \amp 1 \amp 3 \\
2 \amp -3 \amp -1 \\
-1 \amp 3 \amp 4 \\
2 \amp 0 \amp 1 \\
\end{array}\right].
\end{equation*}
\begin{equation*}
\boldsymbol{C} = \boldsymbol{A}\times\boldsymbol{B} = \left[ \begin{array}{cccc}
3 \amp -2 \amp 4 \amp 2 \\
1 \amp 3 \amp -5 \amp -2 \\
\end{array}\right]
\times
\left[ \begin{array}{ccc}
0 \amp 1 \amp 3 \\
2 \amp -3 \amp -1 \\
-1 \amp 3 \amp 4 \\
2 \amp 0 \amp 1 \\
\end{array}\right] =
\left[ \begin{array}{ccc}
-4 \amp 21 \amp 29 \\
7 \amp -23 \amp -22 \\
\end{array}\right]
\end{equation*}
- Element \(c_{11} \text{:}\) Row 1 of \(\boldsymbol{A} \) and column 1 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 0 \\ 2 \\ -1 \\ 2 \\ \end{array}\right] \amp = \amp (3) \times (0) \amp + \amp (-2) \times (2) \amp + \amp (4) \times (-1) \amp + \amp (2) \times (2)\\ \amp = \amp 0 \amp - \amp 4 \amp - \amp 4 \amp + \amp 4 \\ \amp = \amp -4 \end{array} \end{equation*}
- Element \(c_{12} \text{:}\) Row 1 of \(\boldsymbol{A} \) and column 2 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 1 \\ -3 \\ 3 \\ 0 \\ \end{array}\right] \amp = \amp (3) \times (1) \amp + \amp (-2) \times (-3) \amp + \amp (4) \times (3) \amp + \amp (2) \times (0)\\ \amp = \amp 3 \amp + \amp 6 \amp + \amp 12 \amp + \amp 0 \\ \amp = \amp 21 \end{array} \end{equation*}
- Element \(c_{13} \text{:}\) Row 1 of \(\boldsymbol{A} \) and column 3 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 3 \\ -1 \\ 4 \\ 1 \\ \end{array}\right] \amp = \amp (3) \times (3) \amp + \amp (-2) \times (-1) \amp + \amp (4) \times (4) \amp + \amp (2) \times (1)\\ \amp = \amp 9 \amp + \amp 2 \amp + \amp 16 \amp + \amp 2 \\ \amp = \amp 29 \end{array} \end{equation*}
- Element \(c_{21} \text{:}\) Row 2 of \(\boldsymbol{A} \) and column 1 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 0 \\ 2 \\ -1 \\ 2 \\ \end{array}\right] \amp = \amp (1) \times (0) \amp + \amp (3) \times (2) \amp + \amp (-5) \times (-1) \amp + \amp (-2) \times (2)\\ \amp = \amp 0 \amp + \amp 6 \amp + \amp 5 \amp - \amp 4 \\ \amp = \amp 7 \end{array} \end{equation*}
- Element \(c_{22} \text{:}\) Row 2 of \(\boldsymbol{A} \) and column 2 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 1 \\ -3 \\ 3 \\ 0 \\ \end{array}\right] \amp = \amp (1) \times (1) \amp + \amp (3) \times (-3) \amp + \amp (-5) \times (3) \amp + \amp (-2) \times (0)\\ \amp = \amp 1 \amp - \amp 9 \amp - \amp 15 \amp + \amp 0 \\ \amp = \amp -23 \end{array} \end{equation*}
- Element \(c_{23} \text{:}\) Row 2 of \(\boldsymbol{A} \) and column 3 of \(\boldsymbol{B}, \)\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 3 \\ -1 \\ 4 \\ 1 \\ \end{array}\right] \amp = \amp (1) \times (3) \amp + \amp (3) \times (-1) \amp + \amp (-5) \times (4) \amp + \amp (-2) \times (1)\\ \amp = \amp 3 \amp - \amp 3 \amp - \amp 20 \amp - \amp 2 \\ \amp = \amp -22 \end{array} \end{equation*}
Checkpoint 1.2.12. Multiply two matrices.
Find the product of the two given matrices
\begin{equation*}
\boldsymbol{A}= \begin{array}{cc}
\lceil \amp{3} \amp {1} \amp \rceil\\
\vert \amp{2} \amp {-3} \amp \vert\\
\vert \amp{2} \amp {-1} \amp \vert\\
\lfloor \amp{-3} \amp {-1} \amp \rfloor\\
\end{array}, \hspace{1cm}
\boldsymbol{B}= \begin{array}{lrrrr}
\lceil \amp{-3} \amp {-1} \amp {-3} \amp \rceil\\
\lfloor \amp{-4} \amp {-1} \amp {0} \amp \rfloor\\
\end{array}.
\end{equation*}
| \(\,\) | \(\lceil\) | \(\rceil\) | |||
| \(C =\) | \(\vert\) | \(\vert\) | |||
| \(\,\) | \(\vert\) | \(\vert\) | |||
| \(\,\) | \(\lfloor\) | \(\rfloor\) | |||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
Answer 1.
Answer 2.
Answer 3.
Answer 4.
Answer 5.
Answer 6.
Answer 7.
Answer 8.
Answer 9.
Answer 10.
Answer 11.
Answer 12.
Solution.
\(-13\)
\(-4\)
\(-9\)
\(6\)
\(1\)
\(-6\)
\(-2\)
\(-1\)
\(-6\)
\(13\)
\(4\)
\(9\)
\begin{equation*}
\left[ \begin{array}{cc}
{3} \amp {1} \\
{2} \amp {-3} \\
{2} \amp {-1} \\
{-3} \amp {-1} \\
\end{array}\right] \times
\left[ \begin{array}{ccc}
{-3} \amp {-1} \amp {-3} \\
{-4} \amp {-1} \amp {0} \\
\end{array}\right] =
\left[ \begin{array}{ccc}
{-13} \amp {-4} \amp {-9} \\
{6} \amp {1} \amp {-6} \\
{-2} \amp {-1} \amp {-6} \\
{13} \amp {4} \amp {9} \\
\end{array}\right]
\end{equation*}
Insight 1.2.13. Size matters.
In general, not every matrix can be multiplied to any other matrix. Consider the example depicted in the figure below, 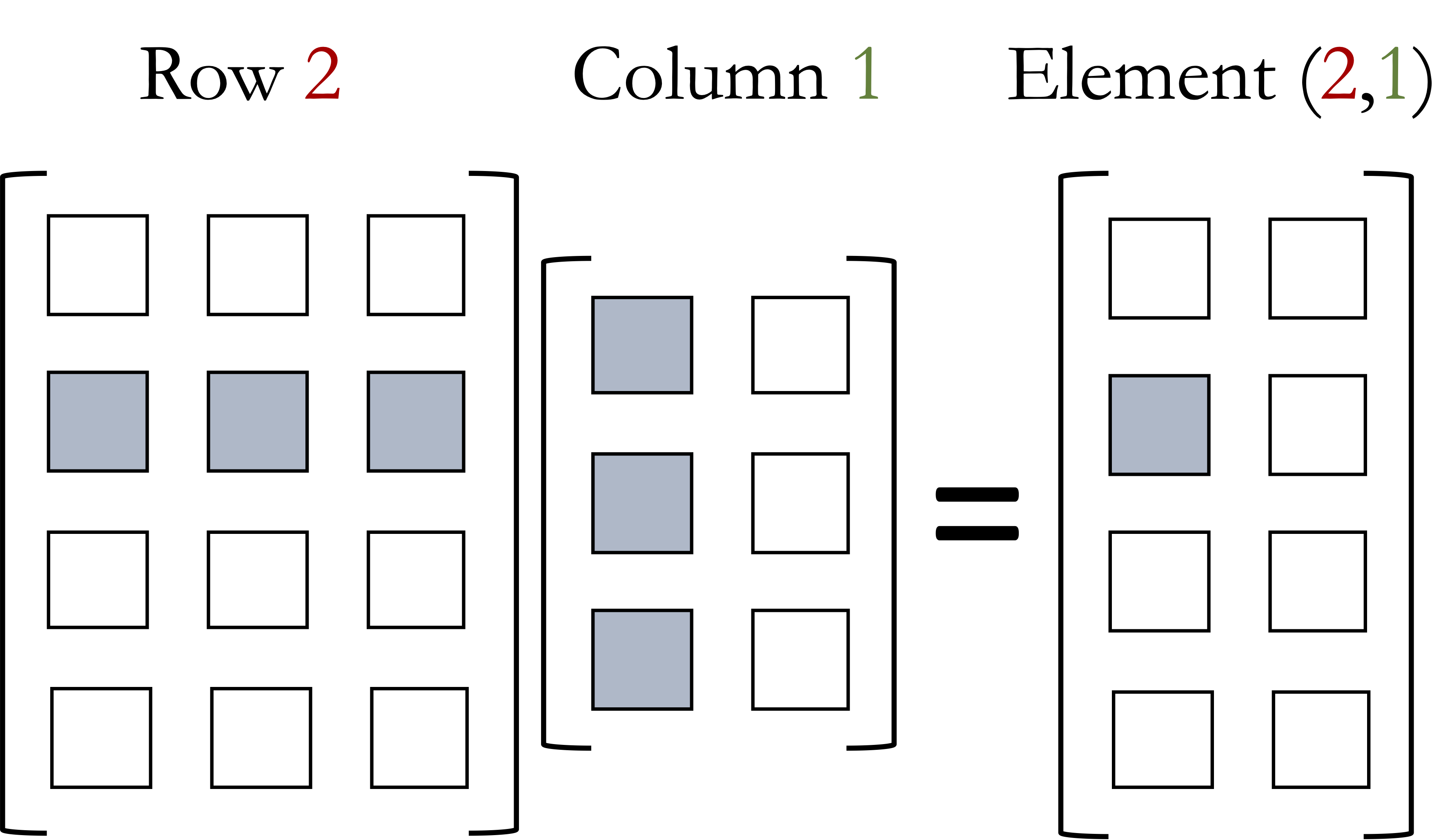 To carry out this operation, we need to multiply the three elements of the row in the first matrix with the three elements of the column in the second matrix.
To carry out this operation, we need to multiply the three elements of the row in the first matrix with the three elements of the column in the second matrix.

If, for instance, the second matrix had 2 rows instead of 3, the operation will be incomplete. 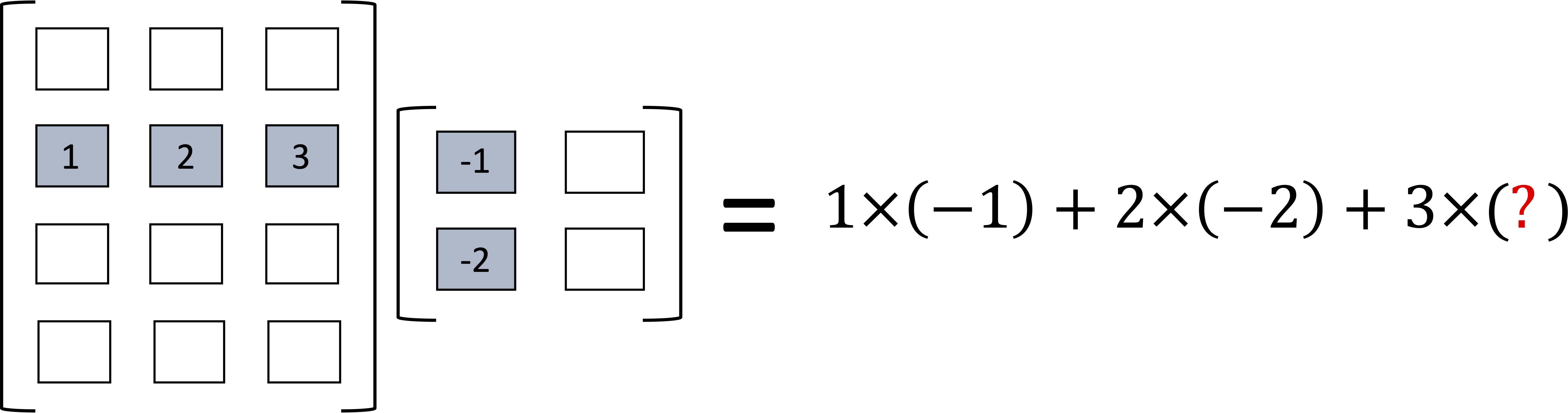
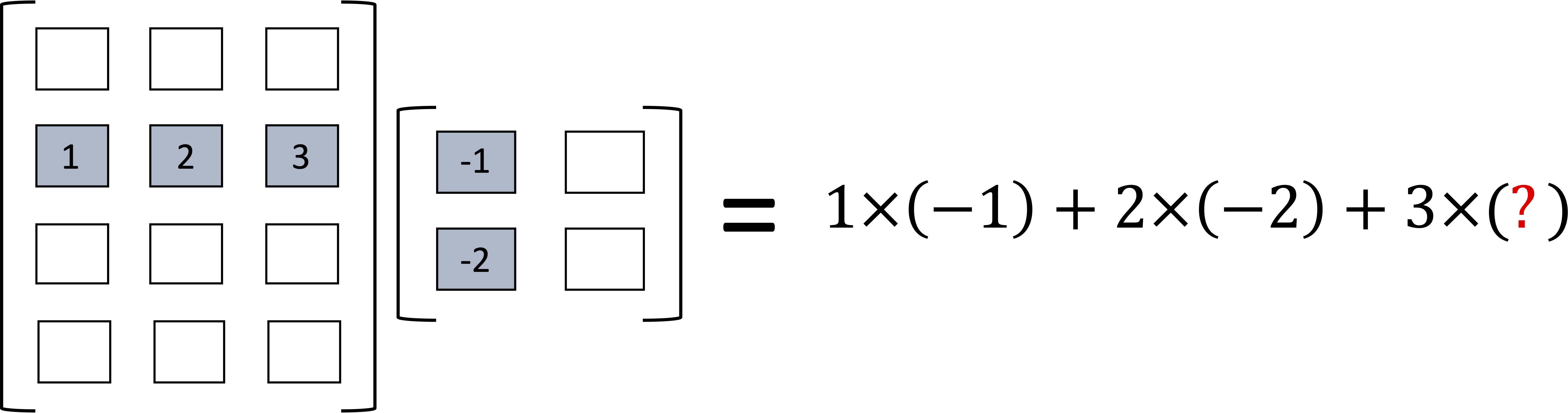
For this reason, we can only multiply matrices that have the "right dimensions." The number of columns in the first matrix must be the same as the number of rows in the second matrix. 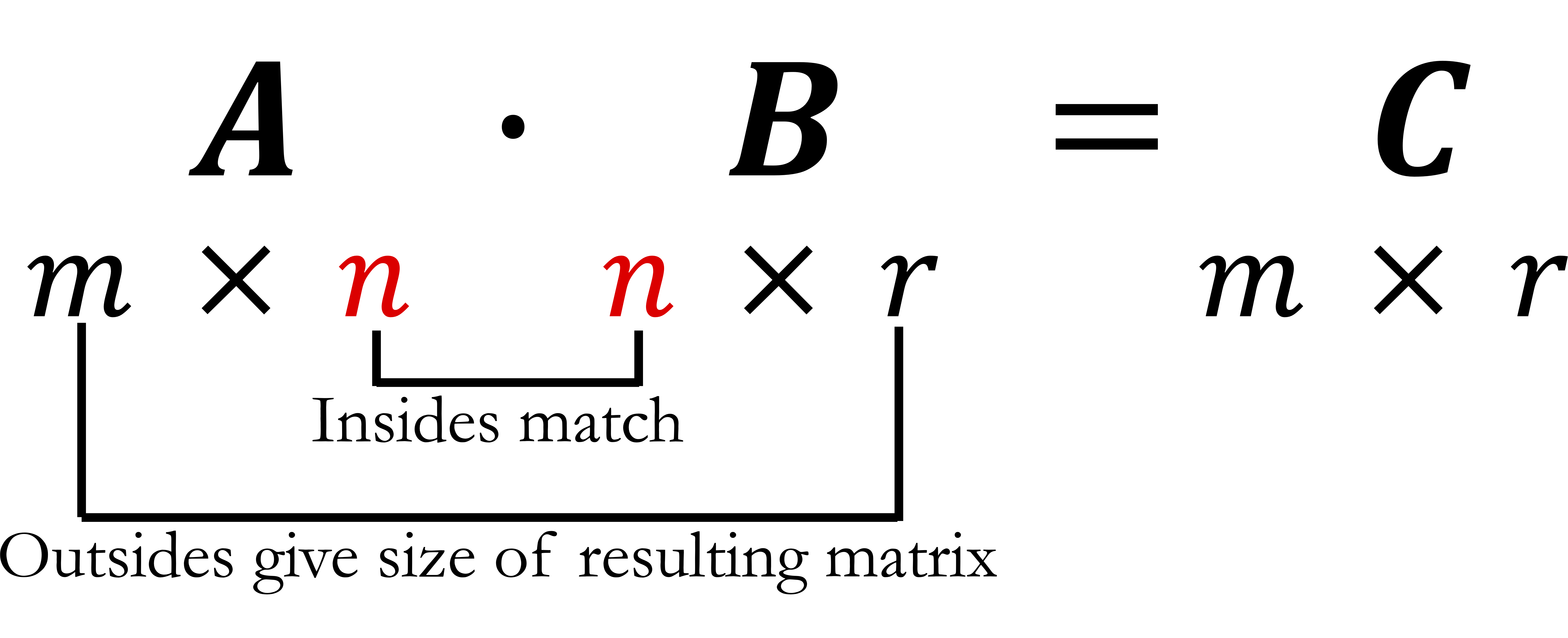
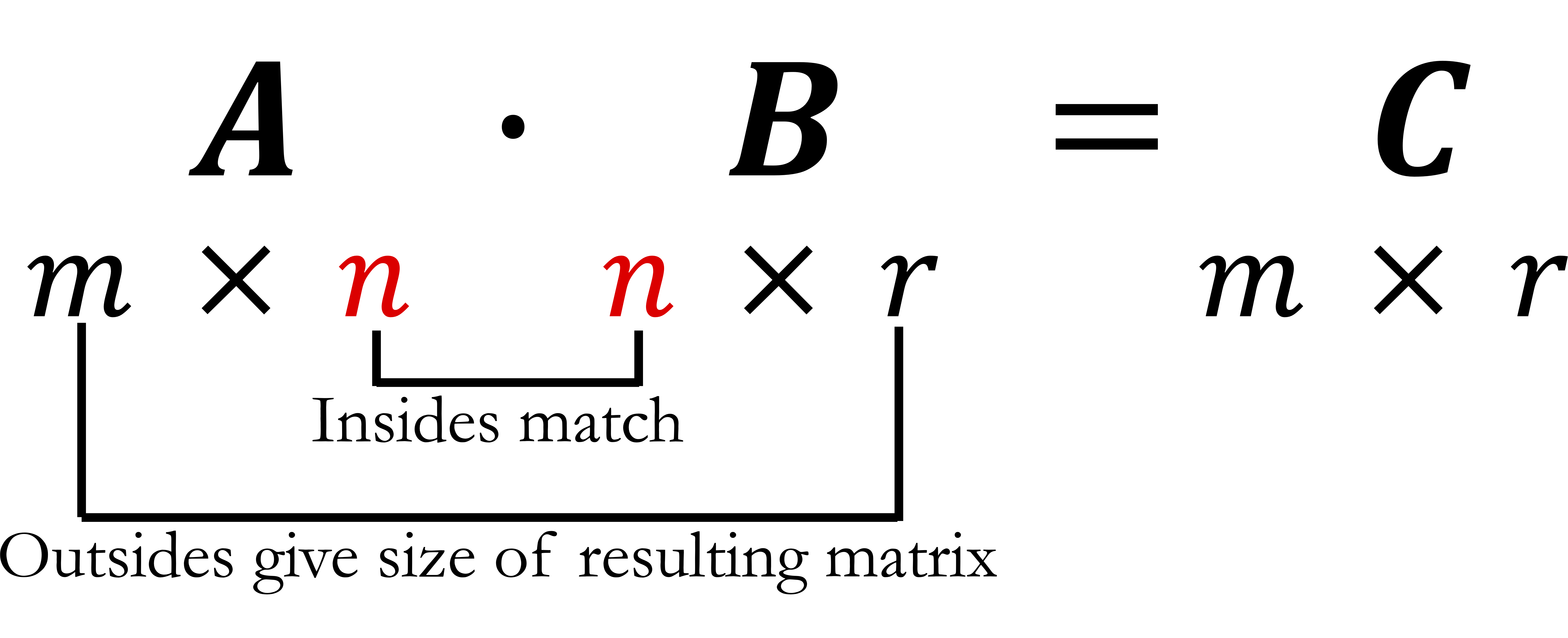
Checkpoint 1.2.14. Matrix multiplication and dimensions.
Determine whether the given multiplication is possible. If possible, give the size of the resulting matrix, if not possible write NA.
-
\(\boldsymbol{A}_{{3} \times {3}} \cdot \boldsymbol{B}_{{8} \times {8}}\)
- Yes
- No
\(\times\) -
\(\boldsymbol{A}_{{8} \times {1}} \cdot \boldsymbol{B}_{{1} \times {9}}\)
- Yes
- No
\(\times\) -
\(\boldsymbol{A}_{{9} \times {3}} \cdot \boldsymbol{B}_{{3} \times {8}}\)
- Yes
- No
\(\times\) -
\(\boldsymbol{A}_{{1} \times {9}} \cdot \boldsymbol{B}_{{8} \times {3}}\)
- Yes
- No
\(\times\) -
\(\boldsymbol{A}_{{3} \times {8}} \cdot \boldsymbol{B}_{{1} \times {8}}\)
- Yes
- No
\(\times\) -
\(\boldsymbol{A}_{{8} \times {1}} \cdot \boldsymbol{B}_{{1} \times {8}}\)
- Yes
- No
\(\times\)
Answer 1.
Answer 2.
Answer 3.
Answer 4.
Answer 5.
Answer 6.
Answer 7.
Answer 8.
Answer 9.
Answer 10.
Answer 11.
Answer 12.
Answer 13.
Answer 14.
Answer 15.
Answer 16.
Answer 17.
Answer 18.
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{Yes}\)
\(8\)
\(9\)
\(\text{Yes}\)
\(9\)
\(8\)
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{Yes}\)
\(8\)
\(8\)


