Subsection 1.1 Matrix basics
In the previous chapter we defined matrices () as arrays of rows and columns, in this section we introduce a convenient notation to work with matrices.
Subsubsection 1.1.1 Matrix size
The size of a matrix is given by the number of its rows and its columns. A \(m \times n \) matrix has \(m\) rows and \(n \) columns. In general, we place the size as a subscript of the name of the matrix, \(\boldsymbol{A}_{m\times n}.\)
\begin{equation*}
\boldsymbol{A}_{2\times3} = \left[ \begin{array}{ccc}
3 \amp 0 \amp -3 \\
2 \amp -4 \amp 5 \\
\end{array} \right]
\hspace{2cm}
\boldsymbol{B}_{3\times1} = \left[ \begin{array}{c}
3 \\ 2 \\-4 \\
\end{array} \right]
\hspace{2cm}
\boldsymbol{C}_{2\times2} = \left[ \begin{array}{cc}
1 \amp -2 \\
0 \amp 3 \\
\end{array} \right]
\end{equation*}
Checkpoint 1.1.2. Size of a matrix.
Give the size for each matrix.
\begin{equation*}
\boldsymbol{A} = \begin{array}{lrrr}
\lceil \amp 3 \amp 2 \amp \rceil\\
\vert \amp 5 \amp 0 \amp \vert\\
\lfloor \amp 1 \amp -3 \amp \rfloor\\
\end{array}
\end{equation*}
The size of \(\boldsymbol{A}\) is \(\times\)
\begin{equation*}
\boldsymbol{B} = \begin{array}{lrrrr}
\lceil \amp -1 \amp 4 \amp 0 \amp \rceil \\
\lfloor \amp 2 \amp 1 \amp 9 \amp \rfloor \\
\end{array}
\end{equation*}
The size of \(\boldsymbol{B}\) is \(\times\)
\begin{equation*}
\boldsymbol{C} = \begin{array}{lrr}
\lceil \amp -1 \amp \rceil\\
\vert \amp 2 \amp \vert \\
\vert \amp 4 \amp \vert\\
\lfloor \amp 8 \amp \rfloor \\
\end{array}
\end{equation*}
The size of \(\boldsymbol{C}\) is \(\times\)
Subsubsection 1.1.2 Matrix elements
We identify the elements in a matrix based on their location with respect to the rows and columns of the matrix, 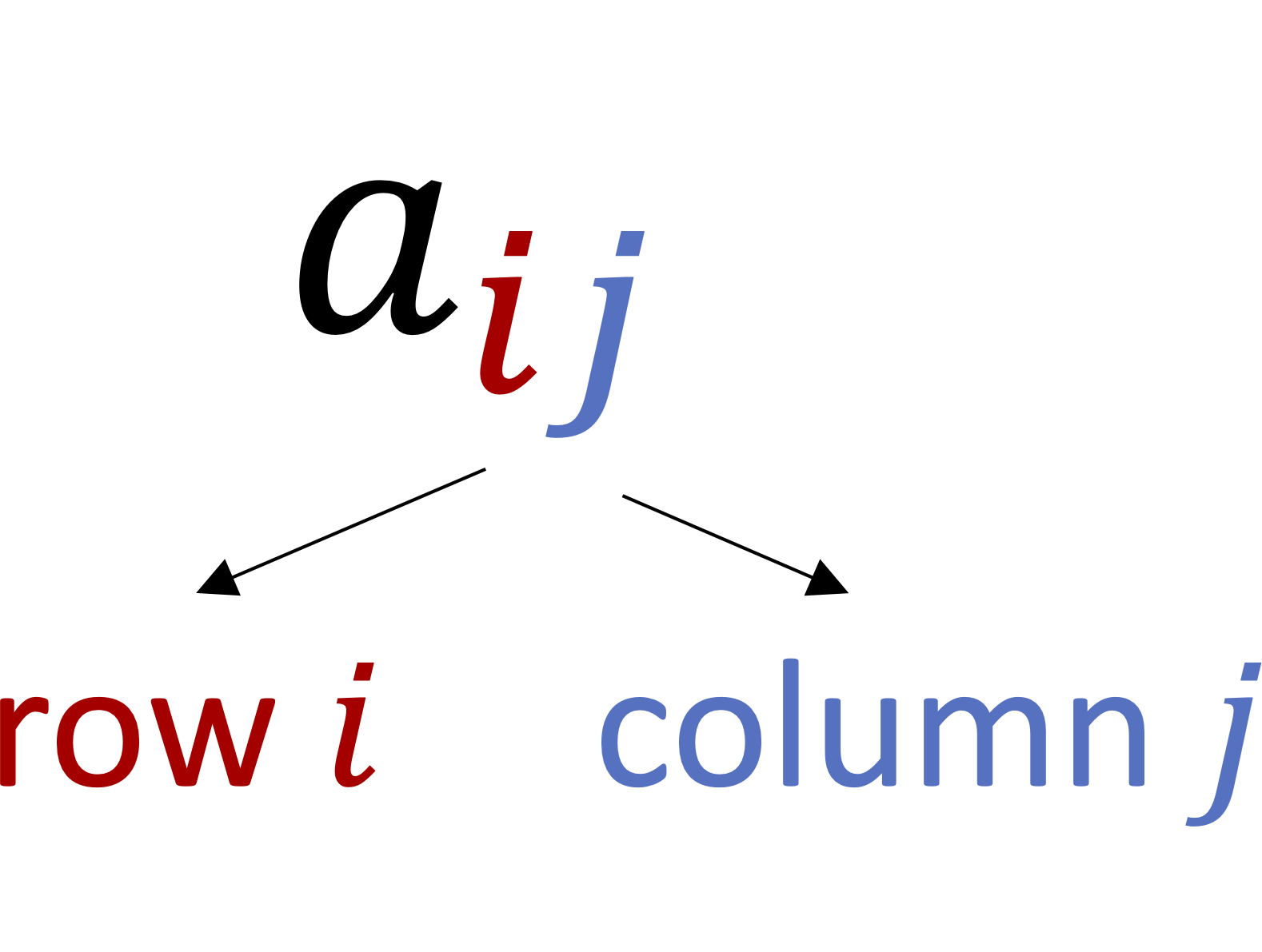

Example 1.1.3. Identifying matrix elements.
For
\begin{equation*}
\boldsymbol{A} = \left[ \begin{array}{rrr}
1 \amp 0 \amp -2 \\
3 \amp -1 \amp 0 \\
6 \amp 7 \amp 1 \\
\end{array} \right]
\end{equation*}
we have
\begin{equation*}
\begin{array}{ccc}
a_{1 2} \amp = \amp 0\\
a_{2 1} \amp = \amp 3\\
a_{3 1} \amp = \amp 6\\
a_{3 2} \amp = \amp 7\\
\end{array}
\end{equation*}
Checkpoint 1.1.4. Matrix elements.
Find the given elements for the matrix.
\begin{equation*}
\boldsymbol{A} = \begin{array}{lrrrr}
\lceil \amp {-5} \amp {-2} \amp {2} \amp \rceil\\
\vert \amp{2} \amp {7} \amp {7} \amp \vert \\
\vert \amp {1} \amp {-4} \amp {-8} \amp \vert\\
\lfloor \amp {8} \amp {-5} \amp {-9} \amp \rfloor\\
\end{array}
\end{equation*}
- \(a_{3 1} =\)
- \(a_{4 3} =\)
- \(a_{1 2} =\)
- \(a_{2 2} =\)
- \(a_{4 1} =\)
Subsubsection 1.1.3 Matrix equality
Two matrices are equal when they have the same numbers in corresponding entries.
\begin{equation*}
\boldsymbol{A} = \boldsymbol{B} \hspace{1cm} \text{If and only if} \hspace{1cm} a_{ij}=b_{ij} \hspace{0.5cm} \text{for ALL } i \text{ and } j's.
\end{equation*}
Subsubsection 1.1.4 Square matrix
A square matrix has the same number of rows and columns, \(m=n. \) The elements of a square matrix \(\boldsymbol{A}_{n\times n} \) where the subscripts are equal \(\left( a_{11}, a_{22}, \cdots, a_{nn}\right) \) are called the matrix main diagonal. 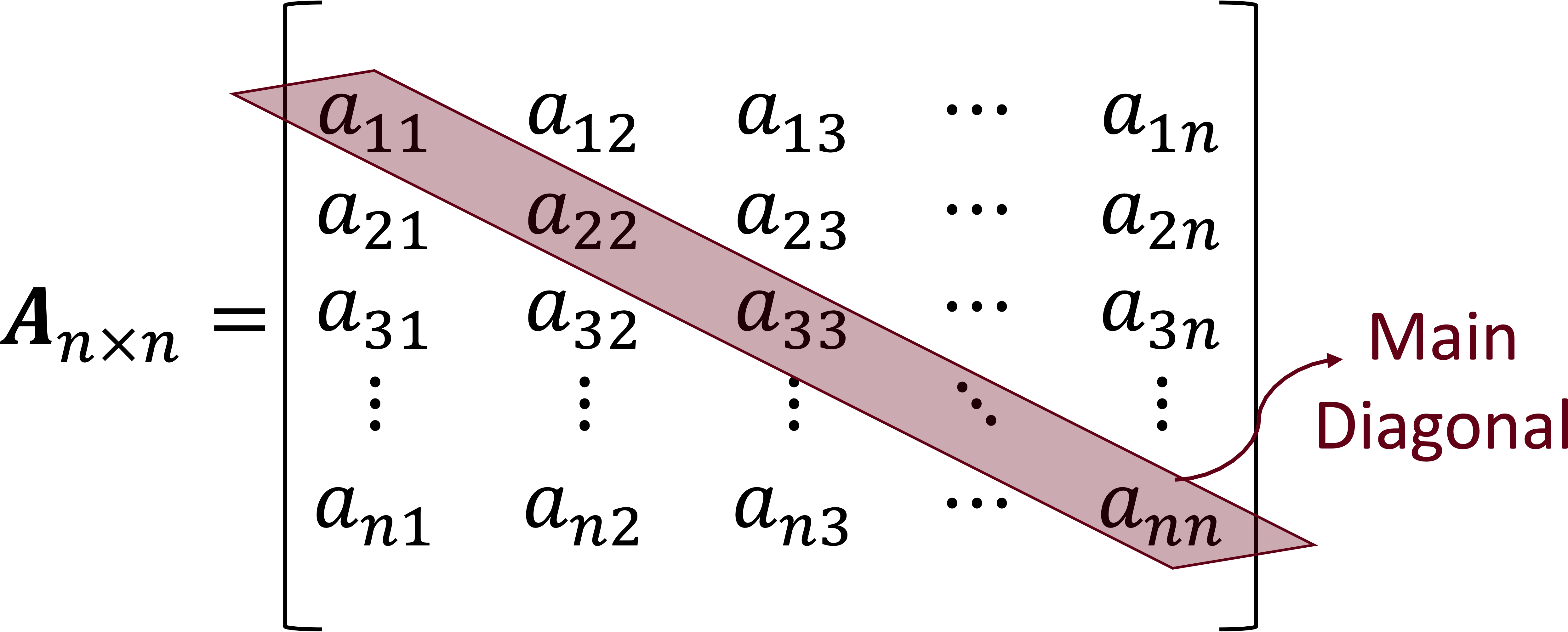

Subsubsection 1.1.5 Identity matrix
An identity matrix is a square matrix with ones in its main diagonal and zeros everywhere else. We use the notation \(\boldsymbol{I}_n \) to indicate an identity matrix that is \(n \times n. \) 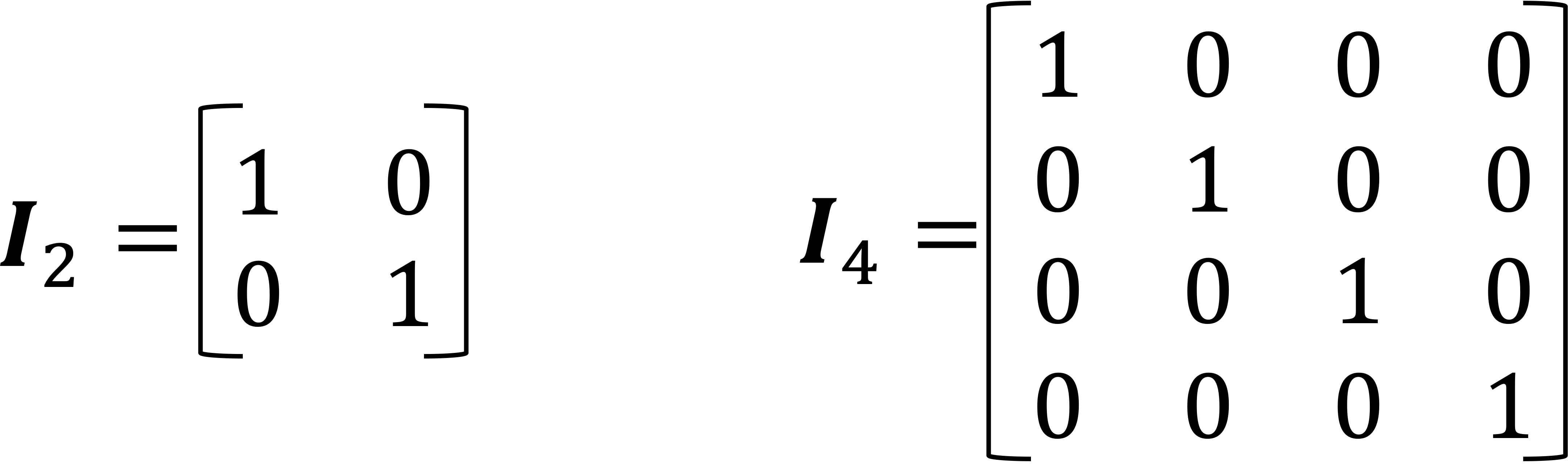
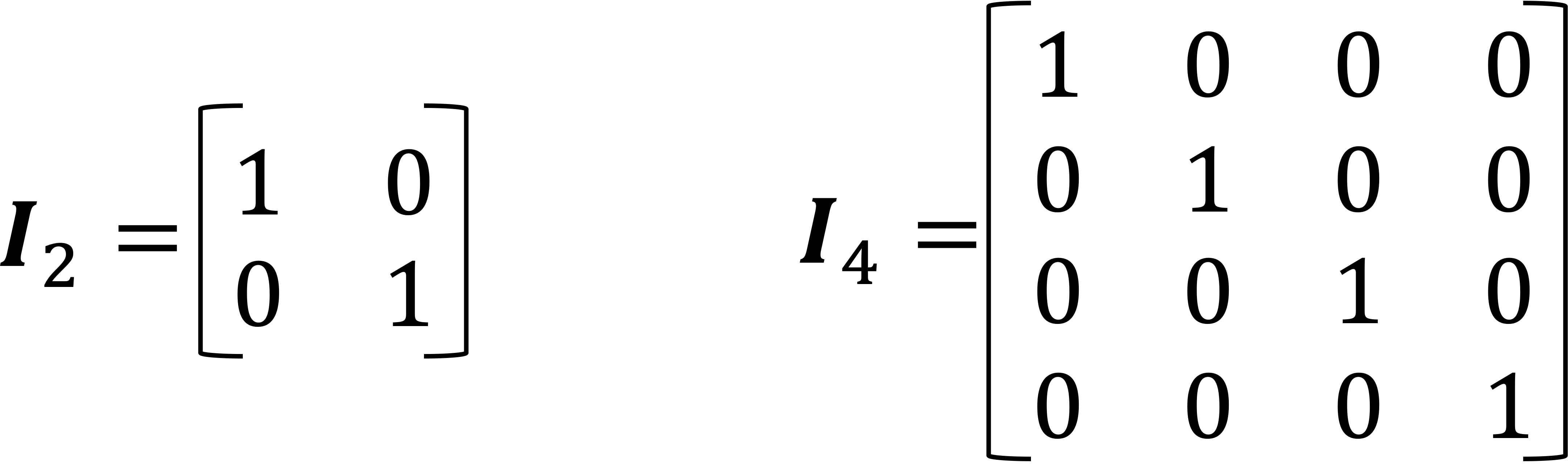
Subsubsection 1.1.6 Zero matrix
A zero matrix is a matrix filled with all zeros and denoted by \(\boldsymbol{0}_{m\times n}. \)


