
Current classes: -
Math 122, Calculus for Business Administration and Social Sciences Mathematics.
Mathematics
532/736I, Modern Geometry.
Office Hours:
- 2:30pm--3:30pm, and by
appointment.
Research Interests:
Differential and integral geometry with excursions into analysis,
convexity, and mathematical relativity.
Preprints and papers:
- On The Existence And Nonexistence Of Stable Submanifolds
And Currents In Positively Curved Manifolds And The Topology Of
Submanifolds In Euclidean Spaces.
with Shihshu Walter Wei.
A revision to appear in
Contemporary Mathematics.
-
Total diameter and the area of closed submanifolds.
with Mohammad Ghomi.
A revision to appear in
Mathematische Annalen.
- Tangent cones and regularity of real hypersurfaces.
with Mohammad Ghomi .
A revision
has appeared in Journal für die reine und angewandte
Mathematik (Crelle's Journal)
- Normal Curvatures of Asymptotically Constant
Graphs and Caratheodory's Conjecture.
with Mohammad Ghomi .
A revision has appeard in
Proceedings of the American
Mathematical Society 140 (2012) pages 4323-4335.
- Nakajima's Problem: Convex Bodies of Constant
Width and Constant Brightness.
with Daniel
Hug.
A revision has
appeared Mathematika 54 (2007) pages 15-24.
- Smooth Convex Bodies with Proportional Projection Functions.
with Daniel
Hug.
A revision has
appeared Israel Journal of Mathematics 159 (2007) pages 317-341.
- Convex Bodies of Constant Width and Constant Brightness.
A revision has
appeared Advances in
Mathematics 204 (2006) pages 241-261.
- Circles Minimize most Knot Energies.
with Aaron Abrams,
Jason Cantarella,
Joe Fu, and
Mohammad Ghomi.
A revision
has appeared in Topology, 42 (2003) pages 381-394.
- A General Theory of Almost Convex Functions.
with Steve Dilworth
and Jim Roberts.
A revision has
appeared in
Transactions of the American Mathematical Society
358 (2006) pages 3413-3445.
- Extremal Approximately Convex Functions and
the Best Constants in a Theorem of Hyers and Ulam.
with Steve Dilworth
and Jim Roberts.
A revision has appeared in Advances in
Mathematics 172 (2002) pages 1-14.
- On Fine Differentiability Properties of
Horizons and Applications to Riemannian Geometry.
with
Piotr T. Chrusciel,
Joe Fu,
and Greg Galloway.
A revision
has appeared in
Journal of
Geometry and Physics 41 (2002) pages 1-12.
- Constructing
Complete Projectively Flat Connections.
A revision has appeared in Rocky Mountain
Journal of Mathematics 35 (2005) pages 1909-1922.
- Solutions Near Singular Points to the
Eikonal and Related First Order
Non-linear Partial Differential Equations in Two Independent
Variables.
with Emil Cornea and
Per-Gunnar Martinsson,
A revision has appeared Differential and Integral
Equations 14 (2001) pages 1441-1468.
- Regularity of Horizons and the Area
Theorem.
with
Piotr T. Chrusciel,
Erwann Delay,
and Greg Galloway.
A revision
has appeared in Annales
Henri Poincaré 2 (2001) pages 109-178.
- On the Size of
Approximately Convex Sets in Normed Spaces.
with Steve Dilworth
and Jim Roberts.
A revision has appeared in
Studia
Mathematica 140 (2000) pages 213-241.
- Towards a Katona Type Proof for the
2-Intersecting Erdös-Ko-Rado Theorem.
with
Gyula
Károlyi
and
László
A. Székely.
A revision
has appeared in Electronic Journal of
Combinatorics
8 (2001) R31
- Extremal Approximately Convex Functions and
Estimating the Size of Convex Hulls.
with Steve Dilworth
and Jim Roberts.
A revision
has appeared in
Advances in Mathematics 148 (1999) pages 1-43.
- A Strong Maximum Principle for Weak Solutions
of Quasi-Linear Elliptic Equations with Applications to Lorentzian
and Riemannian Geometry.
with Lars Andersson
and Greg Galloway.
A revision
has appeared in Communications on Pure and Applied
Mathematics 51 (1998) pages 581-624.
- The Cosmological Time Function.
with Lars Andersson
and Greg Galloway.
A revision
has appeared in
Classical and Quantum Gravity
15 (1998) pages 309-322.
- Comparison and Rigidity Theorems in Semi-Riemannian Geometry.
with Lars
Andersson.
A revision has appeared in Communications in Analysis and
Geometry 6 (1998) pages 819-877.
- The Sharp Sobolev Inequality and the
Banchoff-Pohl Inequality on Surfaces.
A revision
has appeared in Proceedings of the American
Mathematical Society 126 (1998) pages 2779-2787.
- Blaschke's Rolling Theorem for Manifolds with Boundary.
A revision
has appeared in Manuscripta Mathematica 99
(1999) pages 471-483.
- Boundary and Lens Rigidity of Lorentzian Surfaces.
with Lars Andersson
and Mattias Dahl.
A revision
has appeared in Transactions of the American Mathematical Society 348 (1996) pages 2307-2329.
- Processes of Flats Induced by Higher Dimensional Processes III.
with Paul Goodey
and Mark Reeder.
A revision
has appeared in Geometriae Dedicata 61 (1996) pages 257-269
- A Reverse Isoperimetric Inequality, Stability and
Extremal Theorems for Plane Curves with Bounded Curvature.
with Andrejs Treibergs.
A revision has appeared in The Rocky Mountain Journal of
Mathematics 25 (1995) pages 635-684.
- The Kinematic Formula in Riemannian Homogeneous Spaces.
A revision
has appeared in
Memoirs of the American Mathematical Society 106 (1993) no. 509.
- Characterization of Eigenfunctions by Boundedness Conditions.
with
Margaret Reese.
A revision has appeared in Canadian Mathematical
Bulletin
35 (1992) pages 204-213.
- Norms of positive operators on Lp-spaces.
with Anton Schep.
A revision
has appeared in Proceedings of the American Mathematical Society 109 (1990) pages 135-146.
Seminar and class notes:
- Analysis on Homogeneous Spaces.
Notes from a class titled Harmonic Analysis on Homogeneous
Spaces given at the Royal Institute of Technology, Stockholm in the
spring of 1994. They are elementary, incomplete, and disorganized, but
redeem themselves by having lots of miss-prints and an index.
- A Question whose Answer is 42.
A straight tunnel is cut through the Earth, but not
necessary though its center. Arthur Dent starts at rest at one end of
the tunnel and slides, without friction or air resistance and only
under the force of gravity, until he reaches the other end of the
tunnel. Question: How long does the trip take Arthur?
- Customizing Planets to Control Weight.
Given a planet of uniform density and a point on its surface, how can
we reshape the planet to maximize the gravitational force at the given
point.
- The Milnor-Rogers proof of the Brouwer
Fixed Point Theorem.
An exposition of the analytic
proof of Milnor, as simplified by Rogers, of the Brouwer Fixed Point
Theorem. All that is required is the inverse function theorem and the
change of variable formula for multiple integrals.
- A counterexample to one of my favorite
conjectures.
For a smooth compact manifold M let
S(M) be the space of infinitely differentiable real valued
functions on M. Given two manifolds M and N with
dim(M)> dim(N) it is shown that there are injective
linear linear maps of finite order from S(M) to S(N).
I had conjecture that all such maps have infinite dimensional kernel,
which, if it had been true, would have explained many non-injectiveity
results in integral geometry.
- Generic Cut Loci are Dense.
If the set C of compact subsets of Rn is given made
into a metric space using the Hausdorff distance, then set of K
in C with dense cut locus dense in Rn is a dense
G-delta set in C.
- Fubini's Theorem on the Termwise
Differentiable of Series with Monotone Terms.
If f(x)=f1(x)+f2(x)+f3(x)+...
is a pointwise convergent series of function each of which is monotone
increasing, then we give a proof of Fubini's result
that the derivative is given by
f '(x)=f1'(x)+f2'(x)+f3'(x)+...
almost everywhere. This is used to an easy example of function that
is continuous, strictly increasing, but has derivative zero almost
everywhere.
- Mohammad Ghomi's Solution to the
Illumination Problem.
An exposition of a recent result of Mohammad Ghomi who
has shown that if M is smooth compact
oriented surface in R3 so that all the shadow sets
of M are simply connected, then M is the boundary of a
convex set. Also given is his example showing that "simply connected"
can not be weakened to "connected".
- Characterization of Tantrix
Curves.
Let c(t) be a regular curve in the Euclidean space
R3. Then the tantrix is the curve on the
sphere S2 given by
t(t)=c'(t)/|c'(t)|. A proof of a folk theorem
characterizing the tantrix curves of closed curves is given and
extended to higher dimensions and the case of curves symmetric with
respect to a group action.
- The Geometry of Shadow Boundaries on
Surfaces in Space.
If a light is shined on a surface, the boundary between the light and the
shadow is the shadow curve. These are
notes, at an elementary level, on the geometry of shadow curves.
- Alexandrov's Theorem on the Second
Derivatives of Convex Functions.
Notes giving a
detailed proof of Alexandrov's Theorem that a convex suction has second
derivatives almost everywhere. This done by use of Rademacher's
theorem (a Lipschitz function between Euclidean spaces has first
derivatives almost everywhere) whose proof is also included.
- John's Theorem on Ellipsoids in Convex
Bodies.
A proof is given of the result of Fritz John that if K is a convex body
in Rn and E is the ellipsoid of maximum volume in
K then K is contained in c+n(K-c).
When K is symmetric about the origin this can be improved so that
K is contained in n1/2E.
- Notes on Extremal Approximately Convex Functions and the Size of Convex Hulls.
An expanded version of a preprint above (written with Steve Dilworth
and Jim
Roberts). The differences are extra figures, some exposition of results
in the literature, and an alternate proof of one theorem.
- Upper Bounds for the Concentration
Function in Combinatorial Number Theory.
Some notes based on lectures of
Kostya Oskolkov
giving a simplified proof of a theorem of Halász bounding the
number of points a "random" sum of a set of n vectors,
not clustered about any hyperplane, that can lie in a
sufficiently small set.
- The Gronwall Inequality for Solutions
to Ordinary Differential Equations.
A version of the Gronwall inequality that estimates the difference
between solutions to two differential equations in terms of the
difference between their initial conditions and how how much the two
equations differ.
- The Loewner-Pu Inequality, Isosystolic
Constants, and Quasi-Conformal Geometry.
The
Loewner-Pu inequality is generalized to Riemannian metrics g on
an n dimensional torus Tn that are
C-quasi-conformal to a flat metric where the resulting inequality
relates C and some isosytolic constants. For n >
2 this can be combined with recent results of Babenko and Katz to
give examples of smooth metrics that have arbitrarily large
"quasi-conformal distance" from the set of flat metrics on
Tn.
- The Sharp Sobolev Inequality on
Surfaces.
This is a preliminary and expanded version of one of the preprints above.
It also contains an extra section giving a strengthened version of
McKean's lower bound on the first eigenvalue of the Laplacian on a
negatively curved surface.
- The Inverse Function Theorem for
Lipschitz Maps.
This is an edited version of a proof, in the from of exercises with
detailed hints, of the classical inverse function and the inverse
function theorem for Lipschitz maps between Banach spaces that was
given to a graduate class in differential equations as homework.
- Closed Riemannian Manifolds without Conjugate Points.
A self contained proof of the theorem of E. Hopf
that a Riemannian metric on the two dimensional torus without
conjugate points is flat. An extension to higher dimensions, due to
L. Green, is also given. The proof follows that of Green.
- Gunther's Proof of the Nash Isometric imbedding Theorem.
A very elementary account of the local
version of the Nash isometric embedding theorem using the method of
Gunther.
- Kuiper's Theorem on Conformally Flat Compact Manifolds.
A proof of the result of Kuiper that a
compact simply connected locally conformal flat Riemannian manifold is
globally conformally equivalent to the standard sphere. The proof
here, while it follows the basic outline of Kuiper's proof, requires
less smoothness of the metric.
- Estimates on the
Graphing Radius of Submanifolds and the Inradius of Domains.
If all principle curvatures of a complete hypersurface M of
Euclidean space Rn have absolute value at
most one then at any point of M the graphing radius is at least
one. This is used to prove results on the inradius of domains in
terms of the topology and the size of the principle curvatures.
- A Rigidity Theorem for Convex Surfaces.
If M is a two dimensional sphere with a Riemannian
metric that has curvature in the interval [0,1] then every simple closed
geodesic of M has length at least
2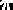 with equality iff M is either
a standard sphere or a capped cylinder.
with equality iff M is either
a standard sphere or a capped cylinder.
Dissertations of Students:
- Somasundaram Velummylum:
The Calculus of Variations and
Zoll Surfaces.
Master's Degree 1990.
- Shiying Zhao:
On the Boundary Behavior of Subharmonic
Functions in Nontangential Acessible Domains.
Ph.D 1991. (Supervised jointly with Manfred Stoll.)
- Louis Kenneth Reinitz:
The Periodic Symmetry Groups of the
Plane.
Master's Degree 1991.
- Gary Allen Cohen:
Intersection Theory.
Master's Degree 1991.
- Aseem Raval:
Mathematics Related to Spinning
Tops.
Master's Degree 1999.
- Michael S. Venn:
Analysis on Finite Gel'fand Spaces.
Master's Degree 2001.
- Anamaria Rusu:
Determining Starlike Bodies by Their
Curvature Intgrals.
Ph.D 2008.
Contact information:
- E-mail:
- howard@math.sc.edu
- Office:
- LeConte
304
- Mail:
- Ralph Howard
Department of Mathematics
University of South Carolina
Columbia, SC 29208
USA
- Telephone:
- (803) 777-7471
- FAX:
- (803) 777-3783
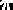 with equality iff M is either
a standard sphere or a capped cylinder.
with equality iff M is either
a standard sphere or a capped cylinder.
