Grant Acknowledgement
I am grateful to have received support from Department of Energy (DOE), National Science Foundation (NSF), Office of Naval Research (ONR), and University of South Carolina (USC).- NSF-DMS 2513112, Co-PI, 2025-2028, $249,949.
- NSF-DMS 2245097, Co-PI, 2023-2026, $599,999.
- USC OVPR ASPIRE-I, PI, 2023-2024, $15,000.
- ONR-N00014-22-1-2624, Co-PI, 2022-2025, (USC share) $69,099.
- NSF-DMS 2012469, Co-PI, 2020-2024, $224,607.
- DE-SC0020270, Co-PI, 2019-2022, $375,000.
- NSF-DMS 1913073, PI, 2019-2022, $167,916.
- USC OVPR ASPIRE-I, PI, 2019-2020, $14,590.
- NSF-DMS 1748357, PI, 2018, $7,280.
- DE-SC0016540, Co-PI, 2016-2019, $584,495.
- NSF-DMS 1522672, PI, 2015-2018, $111,258.
- USC OVPR ASPIRE-I, PI, 2015-2016, $13,989.




Research
My research centers around the development of mathematically justified models and corresponding efficient, accurate algorithms for grand challenge problems at the frontier of computational science and engineering.
Industrial Mathematics
|
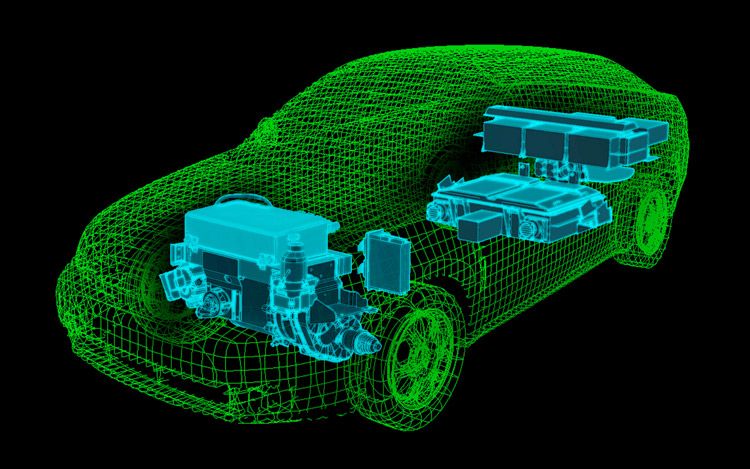
As an IMA industrial postdoc, I used and developed mathematical tools for important industrial projects, such as, optimal power management in plug-in hybrid electric vehicles (PHEVs) and inverse photolithography. |
Reduced-Order Modeling
|
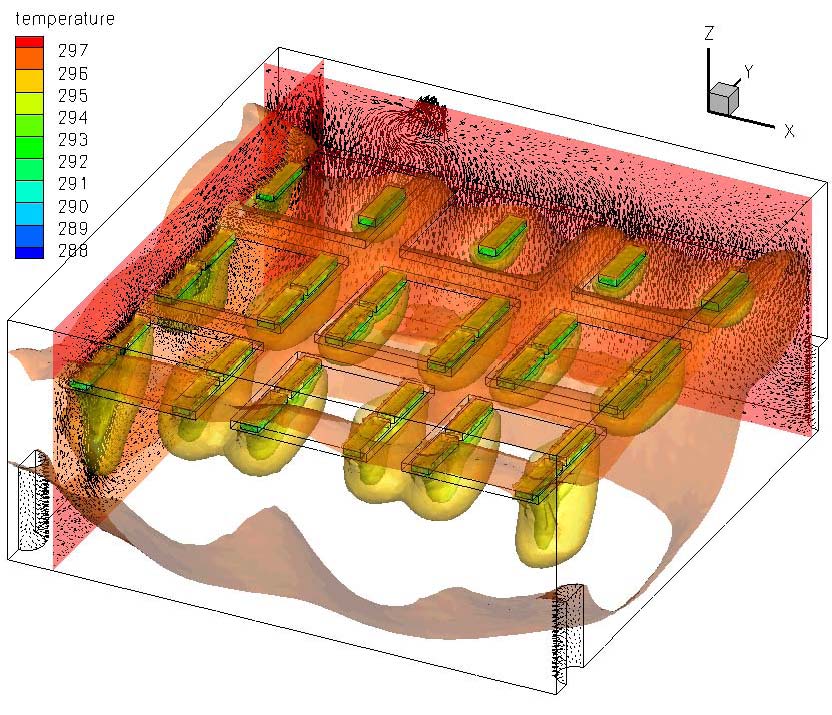
Reduced-order modeling is a powerful technique to decrease the tremendous computational cost required in many real-world problems, e.g., the control of complex flows. The proper orthogonal decomposition (POD) combined with Galerkin method has been widely used to generate reduced-order models (ROMs) for flows. Unfortunately, this methodology breaks down when the complexity of the flow increases. To address the lack of physical accuracy of standard POD-ROMs, novel POD closure models were introduced for structurally dominated turbulent flows. |
Climate Modeling
|
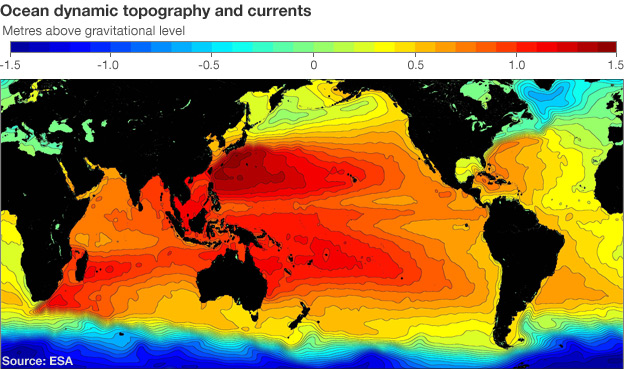
Simplified models for geophysical flows have been developed in climate modeling because various physical processes and long time integration need to be considered. The main challenge is the tradeoff between computational efficiency and physical accuracy. We developed an Approximate deconvolution large eddy simulation model for the quasi-geostrophic equations, which are used to describe the double-gyre circulations characterizing mid-latitude ocean basins. |
Numerical Analysis

|
To understand and further improve the new models, numerical analysis has been used
to design and analyze associated discretization algorithms.
(i) We developed sound foundations for the new POD-ROM closure models,
by extending the finite element method theoretical framework to the POD setting and providing rigorous error estimates
that yielded insight into the optimal model parameter choices;
(ii) We analyzed a high-order ( C1 ) finite element discretizations of the quasi-geostrophic equations; (iii) We proposed a high-order discontinuous Galerkin method for the approximations of linear functionals. |