Climate Modeling
Climate modeling is a grand challenge computational problem, a research topic at the frontier of computational science. Simplified models for geophysical flows have been developed aim to: capture the important geophysical structures, while keeping the computational cost at a minimum. Although successful in numerical weather prediction, these models have a prohibitively high computational cost in climate modeling, where different physical processes and long time integration need to be considered. Thus, there is a clear need for computationally efficient mathematical models and numerical discretizations for climate modeling. The main challenge is the tradeoff between computational efficiency and physical accuracy.
As a first step in developing computationally efficient numerical discretizations for the ocean and the atmosphere, we considered the quasi-geostrophic equations, which describe double-gyre circulations characterizing mid-latitude ocean basins. For the QGE, we considered the streamfunction-vorticity formulation:
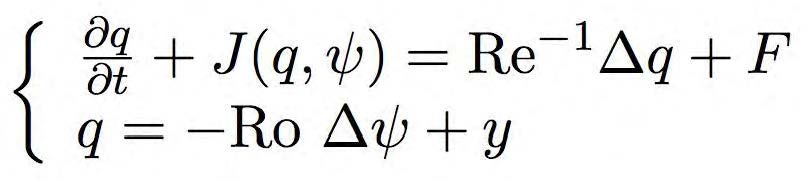
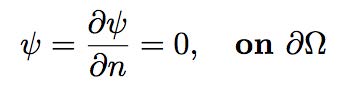
Here, Ro is the Rossby number, Re is the Reynolds number,
ψ is the streamfunction, q is the potential vorticity,
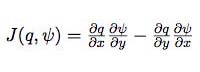 is the Jacobian,
F is the external forcing and β y measures the beta-plane effect from the Coriolis force due to rotation.
is the Jacobian,
F is the external forcing and β y measures the beta-plane effect from the Coriolis force due to rotation.
We developed an LES approximate deconvolution model that decreased the computational cost of the DNS simulation by an order of magnitude without compromising the physical accuracy.
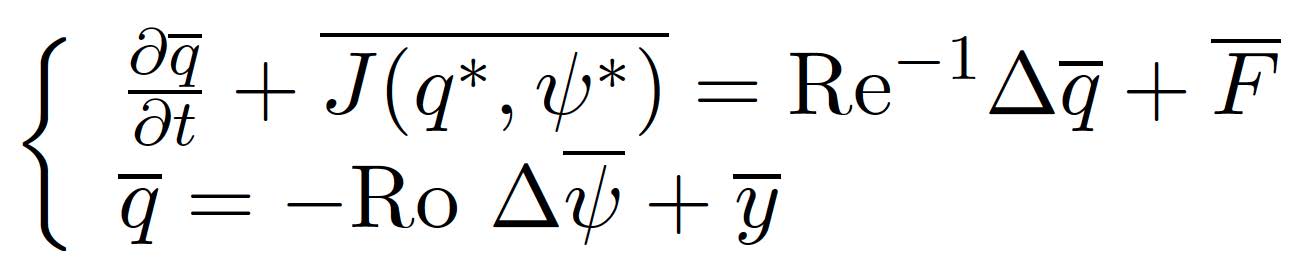
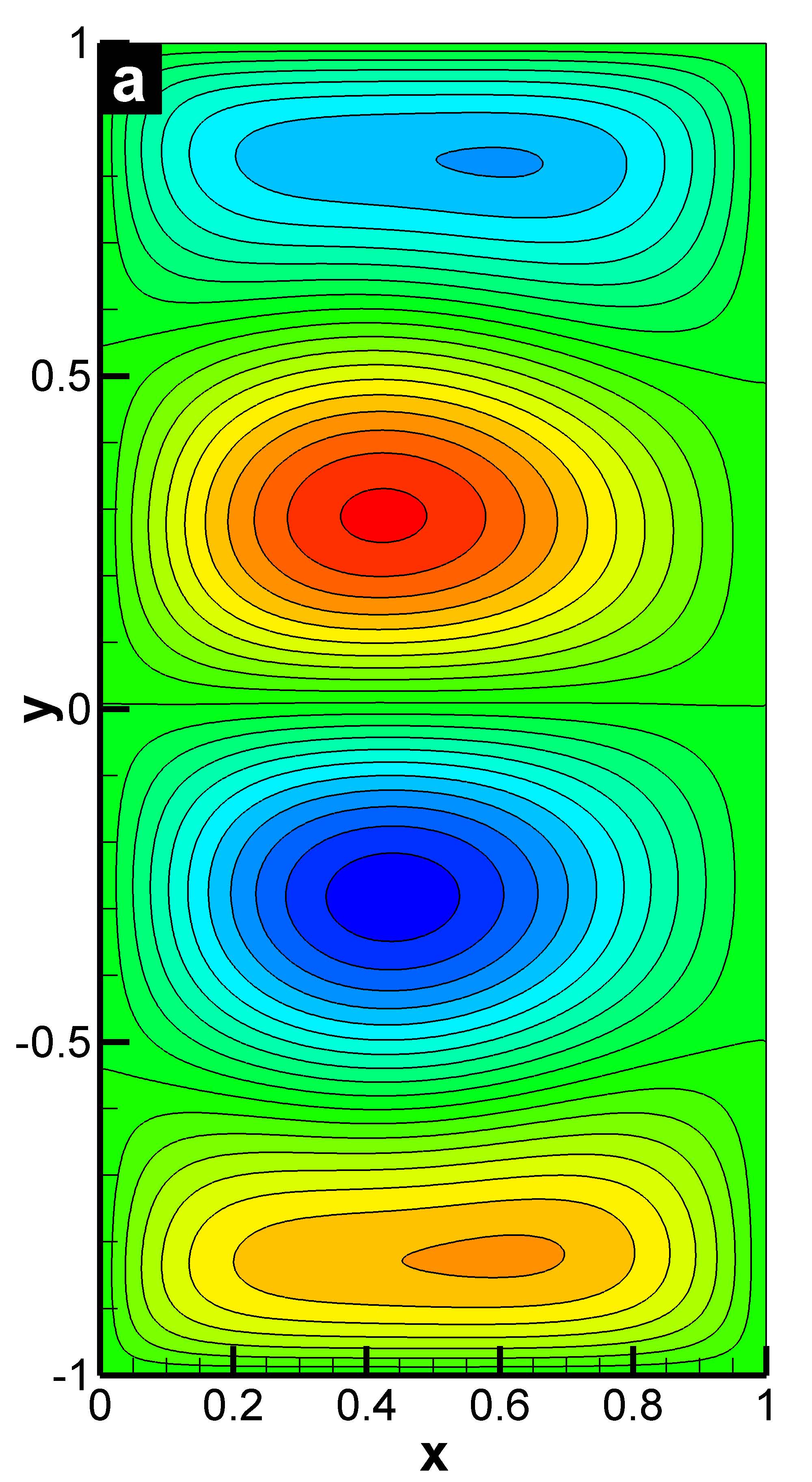
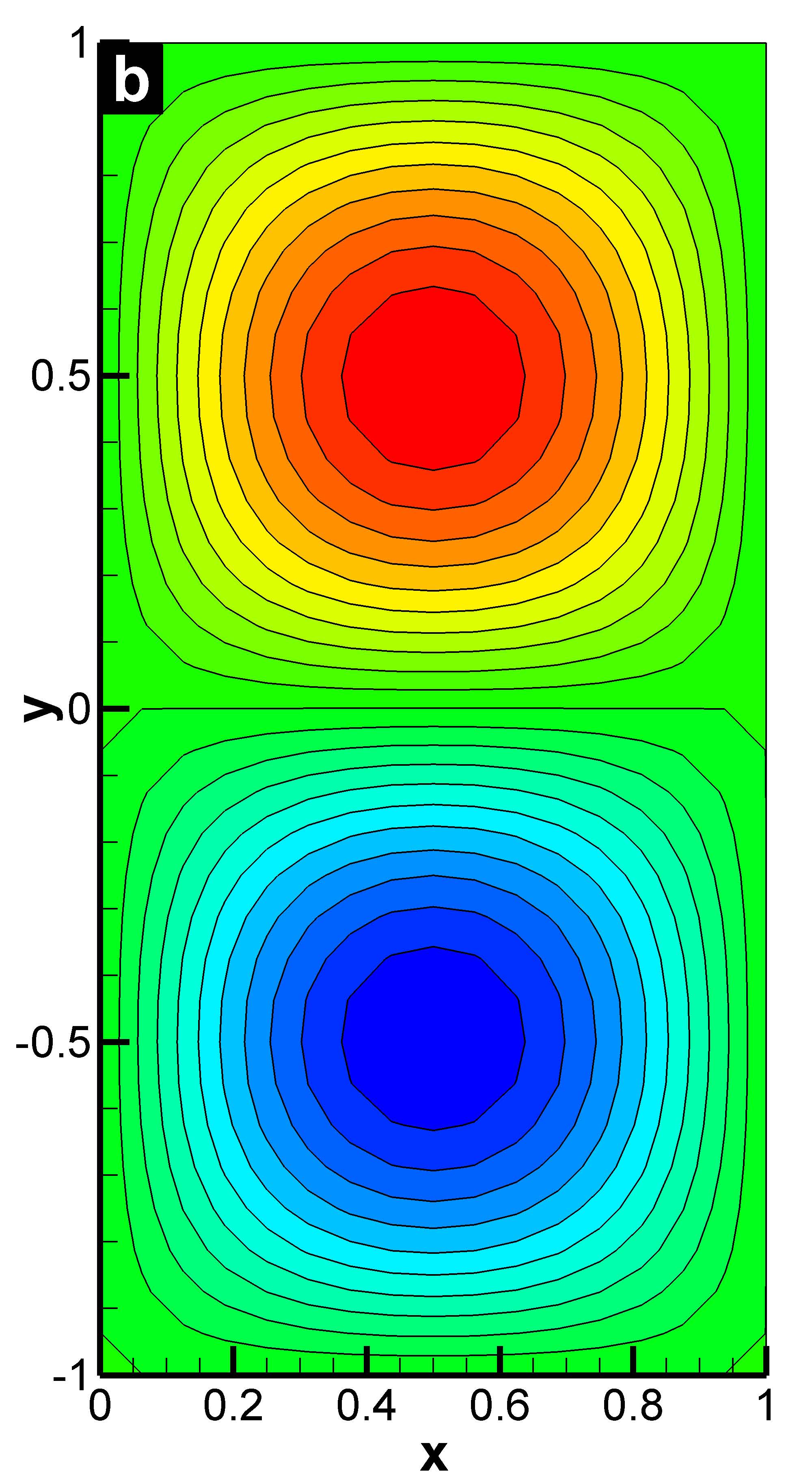
The temporal average of the streamfunction clearly shows that the QGE on a coarse mesh leads to nonphysical results, whereas the AD model obtains results that are qualitatively close to those from the DNS. This is the first time that the AD methodology, which has a sound mathematical foundation, has been employed in the numerical simulation of realistic large scale geophysical flows.
| 
| 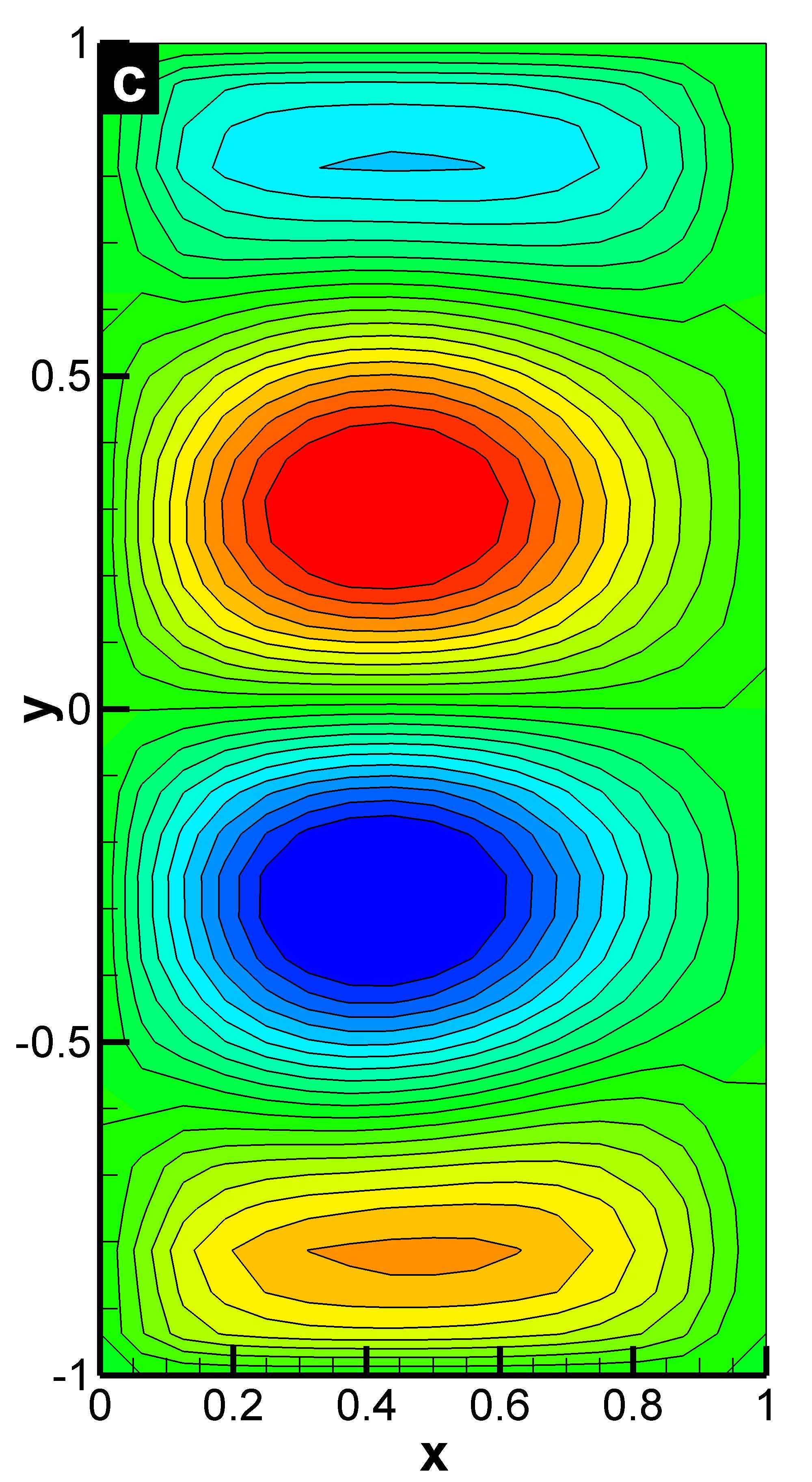
| Double-gyre oceanic circulation modeled by QGE. Time-averaged streamfunction
for Re=450 and Ro=0.0036:
(a) DNS (512 × 256);
(b) under-resolved QGE (32 × 16);
(c) AD model (32 × 16). Note the new AD model yields accurate results on a much coarser mesh. |