Reduced-order Modeling

To address the lack of physical accuracy of standard POD-ROMs, we developed closure models for POD-ROMs, drawing inspiration from state-of-the-art large eddy simulation (LES). Specifically, we introduced novel closure models for POD-ROMs: the variational multiscale (VMS) and the dynamic subgrid-scale (DS). In the numerical simulation of a 3D turbulent flow past a cylinder at a Reynolds number Re=1000, both the VMS and the DS closure models yielded a dramatic increase in the accuracy of the POD-ROMs, while reducing the computational cost of a direct numerical simulation (DNS) by an order of magnitude.

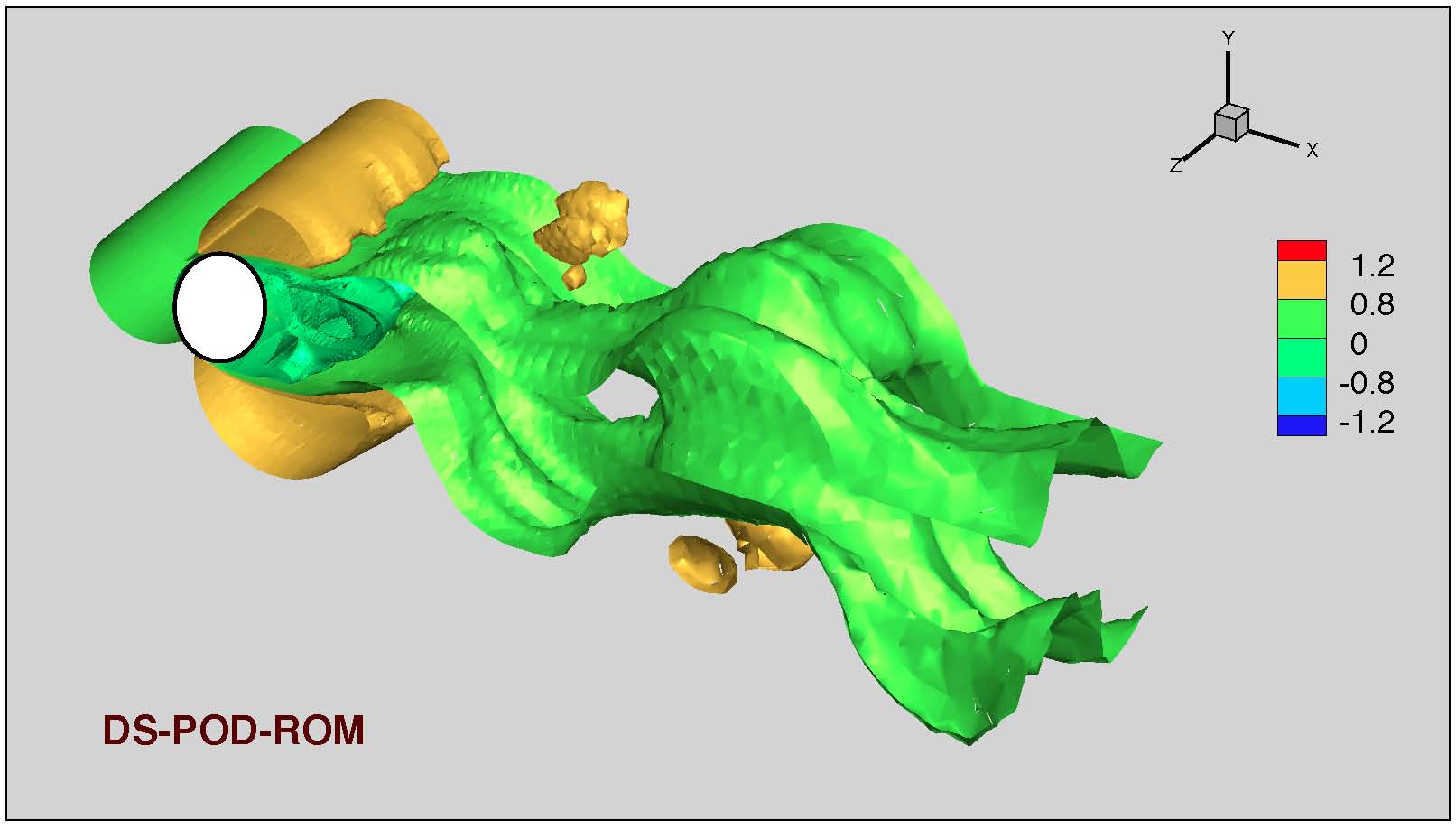
3D turbulent flow simulation at Re=1000. DNS and novel DS-POD closure model results. Note the accurate results obtained with the new POD-ROM. To watch animations, click the right button.

Recognizing that a standard POD discretization of these inherently nonlinear closure models would require the recomputation of the corresponding matrices at each time step and thus significantly increase the computational time, a novel two-level algorithm was designed that computes nonlinear terms efficiently on the coarse mesh, while computing the others on the original fine mesh. The two-level algorithm achieves the same level of accuracy as a standard fine mesh computation, but decreases the computational cost by an order of magnitude. This algorithm allows efficient computational development of realistic, nonlinear state-of-the-art closure models for POD-ROMs.

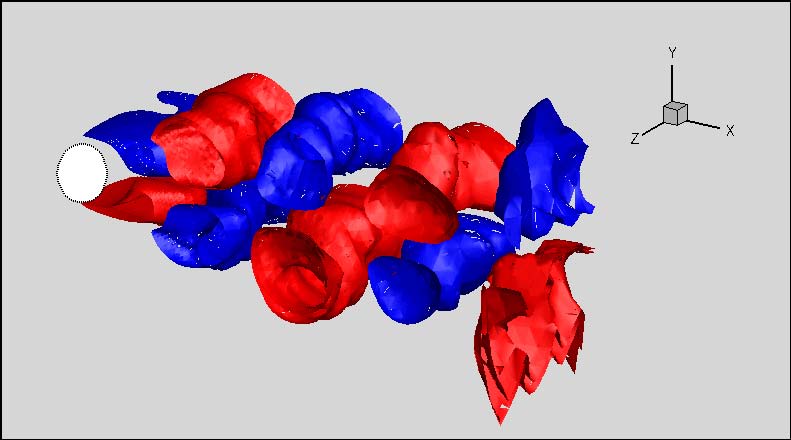
The first streamwise POD mode on a 417,984-node mesh; (right) the novel two-level algorithm on a 26,736-node mesh. Note the large structure is clearly captured, which motivates the two-level algorithm. To watch animations, click the above button.

The third noteworthy achievement was the development of a mathematically sound approach to determine the model parameters in the POD-ROM closure models. Since the usual phenomenological arguments utilized in LES to determine the model parameters are questionable in a POD setting, a fundamentally different methodology was employed. By performing a rigorous error analysis for the finite element discretization, the optimal artificial viscosity coefficient for a VMS closure model was determined. 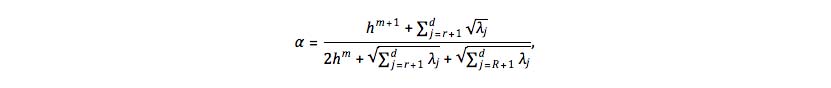    where h is the mesh-size, m is the finite element polynomial interpolation order, λ_j are the singular values of the snapshot matrix, r is the number of POD modes in the model, and R is the number of the POD modes in the secondary Galerkin truncation utilized in the VMS approach.


As a Givens associate, I spent the summers of 2010 and 2011 in the Mathematics and Computer Science Division at the Argonne National Laboratory, where, together with Dr. Mihai Anitescu and Dr. Oleg Roderick , we performed uncertainty analysis of complex simulation models in nuclear engineering.

The obvious need for safety in nuclear engineering represents the main motivation of our uncertainty analysis. The challenge, however, is that a high-dimensional parameter (e.g., heat conductivity, fission, and central temperature in the nuclear reactor) uncertainty for computationally expensive simulations is required. Thus, it is natural to reduce the system's dimensionality by finding the most important uncertainty parameters.

We introduced dimensionality reduction techniques to improve the sampling approach. In the first approach, we utilized the sensitivity analysis information to weight the training set and applied dual-weighted POD to extract the most important uncertainties from the data set. In the second approach, we reduced the system's dimension by extraction of latent factors. To quantify uncertainty, we employed a polynomial regression with derivatives method. The two approaches allowed analysis on a high-dimensional (>100) uncertainty space at a modest computational cost.

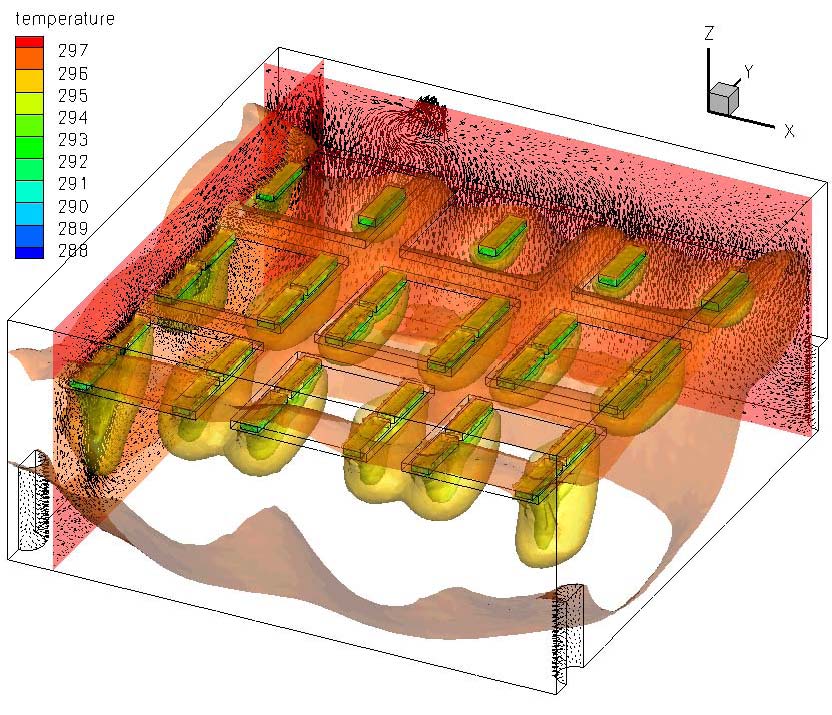As part of the DOE Energy-Efficient Building Systems Design HUB, I have been responsible for developing closure models for POD-ROMs to be used in the airflow optimization and control. Buildings consume 39% of total U.S. energy and, therefore, have a significant impact on the national energy future. To achieve a significant reduction (e.g., 70-80%) in energy consumption, a modern mathematical and computational framework needs to be employed. The structural, spatial and temporal complexity of the system makes a brute force computational approach in the optimization and control impractical.

We have developed and tested several POD-ROM closure models for the Boussinesq equation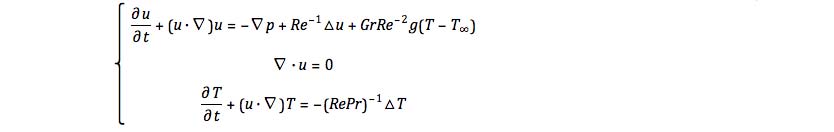s: where u is the velocity, p is the pressure, T is the temperature, T_∞ is the reference temperature, Re is the Reynolds number, Gr is the Grashof number, Pr is the Prandtl number and g is the gravity acceleration. I addressed several new mathematical and computational challenges, such as approximating velocity and temperature fields with different length-scales.