Definition 2.2.1. Systems of linear equations.
A system of linear equations consist of two or more linear equations such that all equations in the system are considered simultaneously.
Section 2.2 Systems of linear equations
\(\, \)
Example 2.2.2. Different types of systems of linear equations.
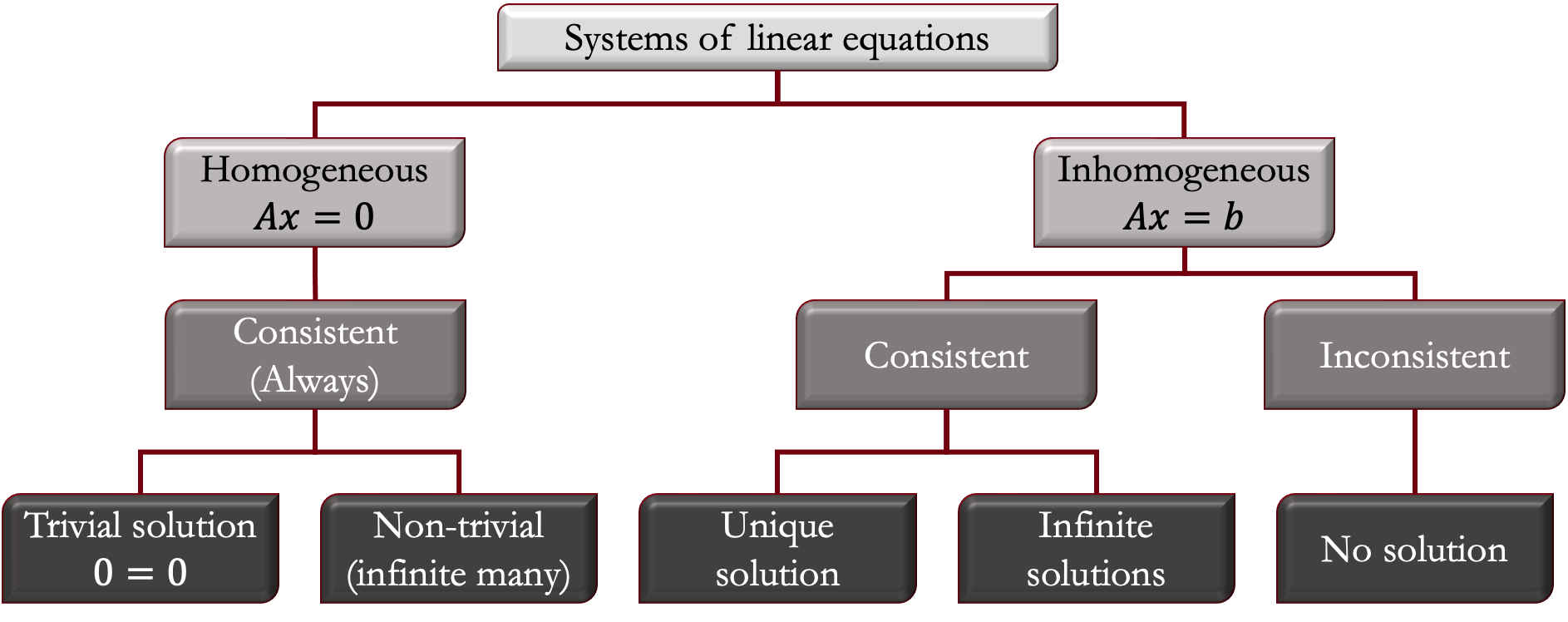
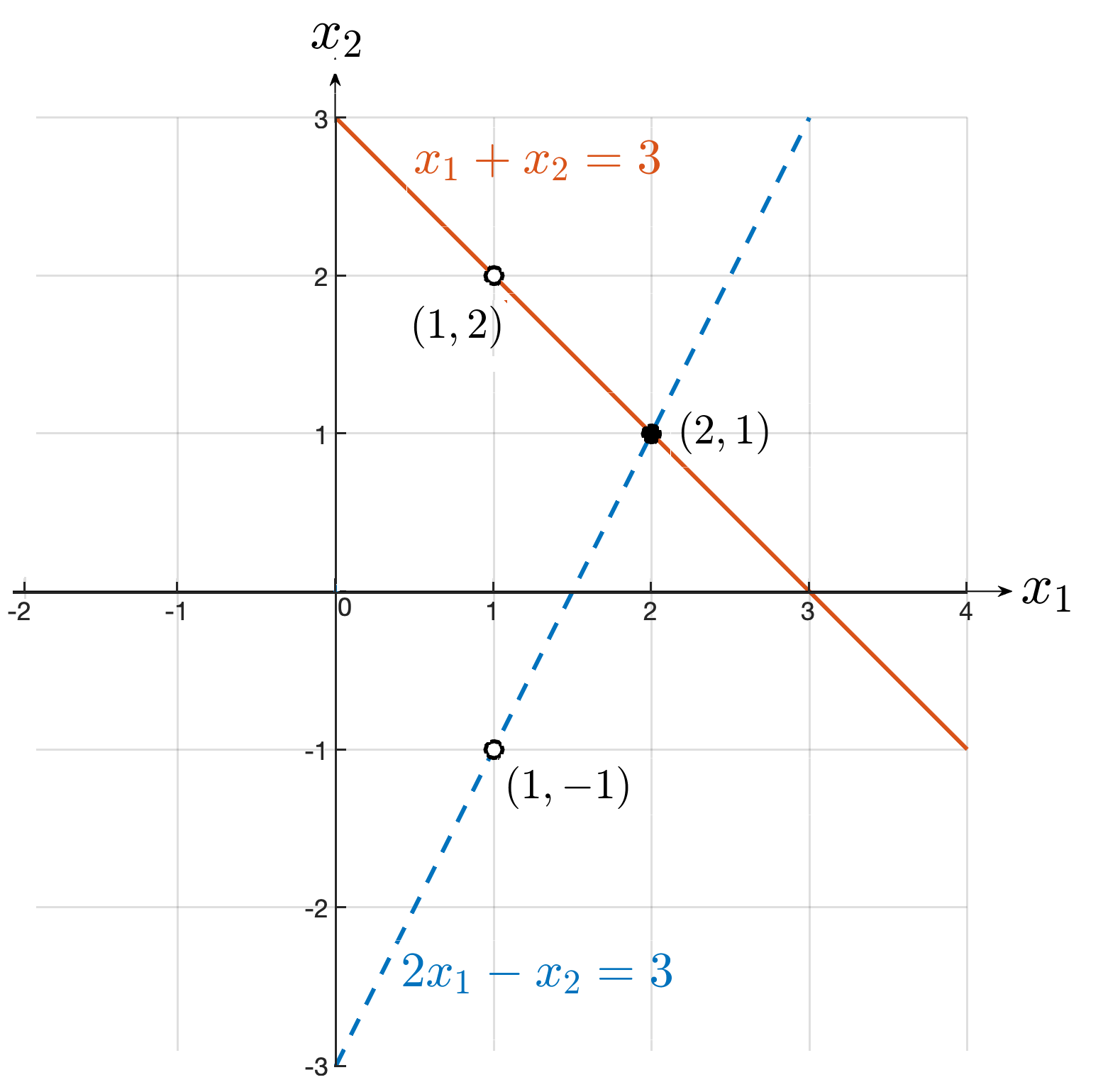The system of linear equations below consists of \(3\) equations of \(2 \) variables,
\begin{equation*}
\left\{\begin{array}{ccccc}
3\, x_1 \amp+\amp 2\, x_2 \amp= \amp -3\\
x_1 \amp-\amp 2\, x_2 \amp= \amp 0\\
2\, x_1 \amp+\amp 3\, x_2 \amp= \amp 1\\
\end{array} \right.
\end{equation*}
The system of linear equations below consists of \(3\) equations of \(3 \) variables,
\begin{equation*}
\left\{\begin{array}{ccccccc}
5\, x_1 \amp+\amp 3\, x_2 \amp - \amp x_3 \amp= \amp 2\\
4x_1 \amp-\amp \, x_2 \amp + \amp 2\,x_3 \amp= \amp -2\\
-2\, x_1 \amp+\amp 4\, x_2 \amp + \amp 4\,x_3 \amp= \amp 0\\
\end{array} \right.
\end{equation*}
\(\, \)
Definition 2.2.3. Homogeneous systems of linear equations.
A system of equations is called homogeneous if each equation in the system is equal to 0.
Example 2.2.4. A \(3 \times 3\) homogeneous system of linear equations.
A homogeneous system of 3 variables and 3 equations has the form
\begin{equation*}
\left\{\begin{array}{ccccccccccc}
a_{11}\, x_1 \amp+\amp a_{12}\, x_2 \amp+\amp a_{13}\, x_3 \amp= \amp 0\\
a_{21}\, x_1 \amp+\amp a_{22}\, x_2 \amp+\amp a_{23}\, x_3 \amp= \amp 0\\
a_{31}\, x_1 \amp+\amp a_{32}\, x_2 \amp+\amp a_{33}\, x_3 \amp= \amp 0\\
\end{array} \right.
\end{equation*}
For some constants \(a_{i,j},\) \(i,j = 1 \dots 3\text{.}\)
\(\, \)
Definition 2.2.5. Solutions to systems of linear equations.
A solution to a system of linear equations are the points that satisfy all equations in the linear system at the same time.
Example 2.2.6. Graphic solutions in 2D - case 1.
Consider the system of equations
\begin{equation*}
\left\{\begin{array}{lcr}
\hspace{0.05cm}x_1 + x_2 \amp=\amp 3\\
2x_1 - x_2 +\amp=\amp 3
\end{array} \right.
\end{equation*}
A solution to the first equation would be \(x_1 = 1, x_2 = 2 \) since
\begin{equation*}
(1)+ (2) = 3 \text{.}
\end{equation*}
However, this is not a solution to the second equation, since
\begin{equation*}
2(1) - (2) - (2) \ne 3 \text{.}
\end{equation*}
Similarly, \(x_1 = 1, x_2 =-1 \) is a solution to the second equation but not to the first. Check!
Then, according to our definition neither set of values is a solution to the system of equations.
A solution to the system of equations is \(x_1 = 2, x_2 = 1 \text{,}\) since
\begin{equation*}
\begin{array}{lcr}
\hspace{0.05cm}(2) + (1) \amp=\amp 3\\
\amp\text{and}\amp\\
2(2) - (1) \amp=\amp 3
\end{array}
\end{equation*}
In this case the system has a unique solution.
Checkpoint 2.2.7. Graphic solutions in 2D - case 2.
Consider the system of linear equations with 2 variables and 3 equations depicted in the figure below.
Does the system have unique solution, infinitely many solutions, or no solution?
- Unique solution
- Infinitely many solutions
- No solution
\(\,\)
Checkpoint 2.2.8. Graphic solutions in 2D - case 3.
Consider the system of linear equations with 2 variables and 2 equations depicted in the figure below.
Does the system have unique solution, infinitely many solutions, or no solution?
- Unique solution
- Infinitely many solutions
- No solution
\(\,\)
Checkpoint 2.2.9. Graphic solutions in 3D.
In previous problems we saw that, in two dimensions, solving a system of linear equations is equivalent to finding the intersection of all the lines within the system. We also know that linear equations in three dimensions correspond to planes. Using what you learned in previous problems and examples, can you determine whether the system depicted below has a unique solution, no solution or infinitely many solutions?
\(\, \)
Definition 2.2.10. Consistent systems of linear equations.
A system of linear equations is called consistent if there exists at least one solution. It is called inconsistent if there is no solution.
Insight 2.2.11. Summary of classification of systems of linear equations.
