Skip to main content

Section 2.1 Basic Definitions

\(\, \)

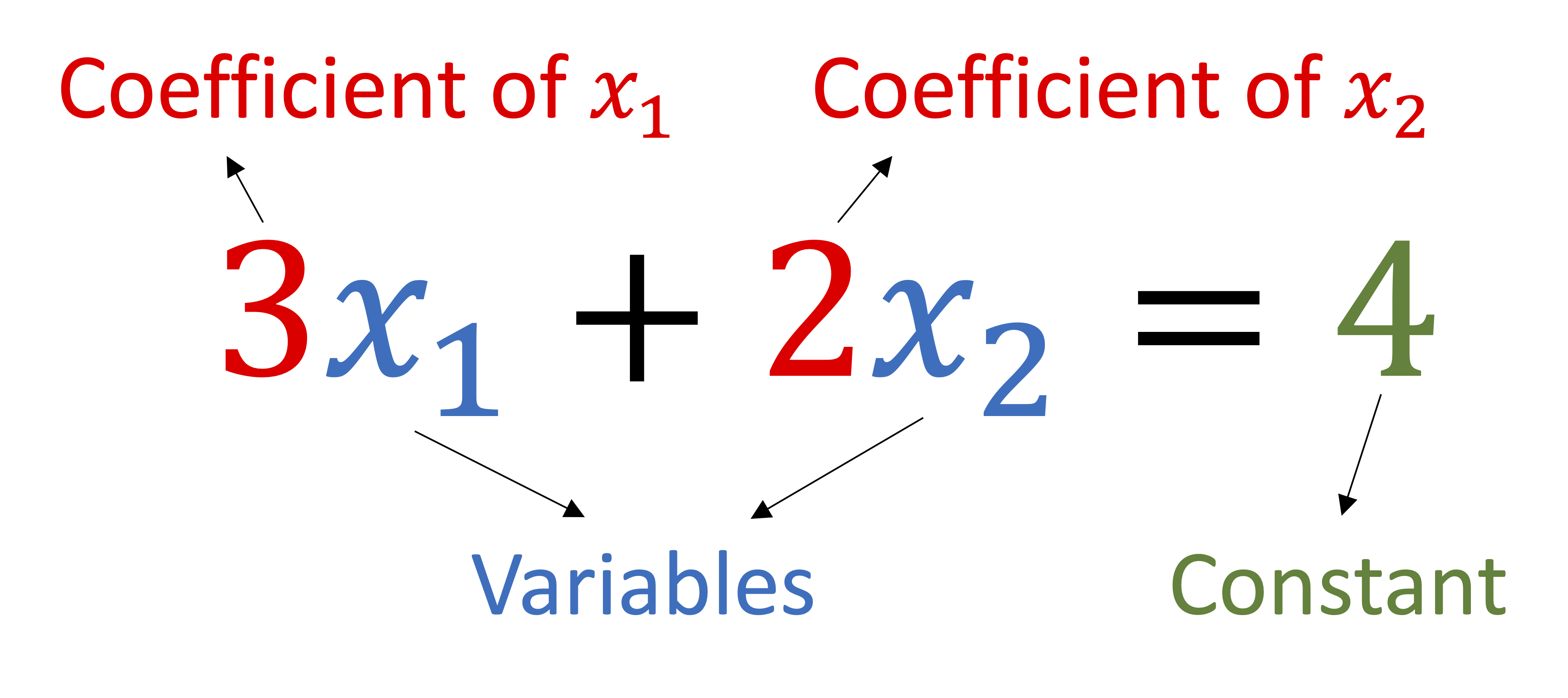
Definition 2.1.1. Linear equations in \(\R^2\).

A linear equation in \(2\) variables \(x_1, x_2 \) is an equation that can be written in the form
\begin{equation*} a_1\,x_1 + a_2\,x_2 = b \end{equation*}
where the coefficients \(a_1\) and \(a_2 \) and the independent variable \(b\) are all constants.
The equation of the line \(y = 3x + 2 \) can be written as
\begin{equation*} -3x_1 + x_2 = 2 \end{equation*}
\(\, \)

Definition 2.1.3. Linear equations in \(\R^3\).

A linear equation in \(3\) variables \(x_1, x_2, x_3 \) has the form
\begin{equation*} a_1\,x_1 + a_2\,x_2 + a_3\,x_3 = b. \end{equation*}
The equation of a plane is also considered a linear equation. For example the equation of a plane given by \(z = -3x + y -2\) can be written as,
\begin{equation*} 3x_1 - x_2 + x_3 = 2 \end{equation*}
\(\, \)
Determine if the given equation is linear (input y or n).
  1. Is \(x = 3y - 2\) Linear?
  2. Is \(y + \sin(x) = 3\) Linear?
  3. Is \(a + b - 3c = 4\) Linear?
  4. Is \(x_1 - x_3+ x_2 = 0\) Linear?
  5. Is \(x_1^2 + x_2 = 3\) Linear?
\(\,\)
Answer 1.
\(\text{Yes}\)
Answer 2.
\(\text{No}\)
Answer 3.
\(\text{Yes}\)
Answer 4.
\(\text{Yes}\)
Answer 5.
\(\text{No}\)
Solution.
1, 3 and 4 are linear. 2 and 5 are non-linear.
The name of the variable does not matter (see 1, 3 and 4) as long as the variables are in linear form the equation is consider linear. The second equation is not linear because the trigonometric function and the last equation is not linear because the first variable is squared.
\(\, \)

Definition 2.1.6. Standard form.

In the standard form of a linear equation all terms containing unknowns are placed in the left-hand-side of the equation and all constant terms in the right-hand-side.
\(\, \)

Definition 2.1.7. Solutions of linear equations.

A point that satisfies a linear equation is considered a solution to that equation.
Consider the equation \(3x_1 + 4x_2 = 21. \)
  1. Is the point \(\left(3, -2 \right)\) a solution to this equation?
  2. Is the point \(\left(0, 2 \right)\) a solution to this equation?
  3. Is the point \(\left(3, 3 \right)\) a solution to this equation?
  4. Is the point \(\left(7, 0 \right)\) a solution to this equation?
\(\,\)
Answer 1.
\(\text{No}\)
Answer 2.
\(\text{No}\)
Answer 3.
\(\text{Yes}\)
Answer 4.
\(\text{Yes}\)
Solution.
Substitute the first coordinate for the first variable \(\left(x_1\right)\) and the second coordinate for the second variable \(\left(x_2\right)\) and if the result is \(21\) then the point is a solution to the linear equation.
Consider the equation \(x_1 - 4x_2 + 3x_3 = -1. \)
  1. Is the point \(\left(-1, 0, 0 \right)\) a solution to this equation?
  2. Is the point \(\left(0, 4, 0 \right)\) a solution to this equation?
  3. Is the point \(\left(-3, 1, 2 \right)\) a solution to this equation?
  4. Is the point \(\left(1, 2, 3 \right)\) a solution to this equation?
\(\,\)
Answer 1.
\(\text{Yes}\)
Answer 2.
\(\text{No}\)
Answer 3.
\(\text{Yes}\)
Answer 4.
\(\text{No}\)
<Prev^TopNext>