Section 1.1 Matrix Operations
Objectives
- Define matrix notation and commonly used matrices.
- Introduce addition and multiplication of matrices.
- Understand algebraic properties of matrix operations.
- Define and learn to find powers of matrices.
\(\, \)
\(\Large{\textbf{Section Content}} \)
\(\, \)
Subsection 1.1.1 Matrix basics
In the previous chapter we defined matrices () as arrays of rows and columns, in this section we introduce a convenient notation to work with matrices.
Subsubsection 1.1.1.1 Matrix size
The size of a matrix is given by the number of its rows and its columns. A \(m \times n \) matrix has \(m\) rows and \(n \) columns. In general, we place the size as a subscript of the name of the matrix, \(\boldsymbol{A}_{m\times n}.\)
Example 1.1.1. Examples of matrix sizes.
Checkpoint 1.1.2. Size of a matrix.
The size of \(\boldsymbol{A}\) is \(\times\)
The size of \(\boldsymbol{B}\) is \(\times\)
The size of \(\boldsymbol{C}\) is \(\times\)
Subsubsection 1.1.1.2 Matrix elements
We identify the elements in a matrix based on their location with respect to the rows and columns of the matrix,
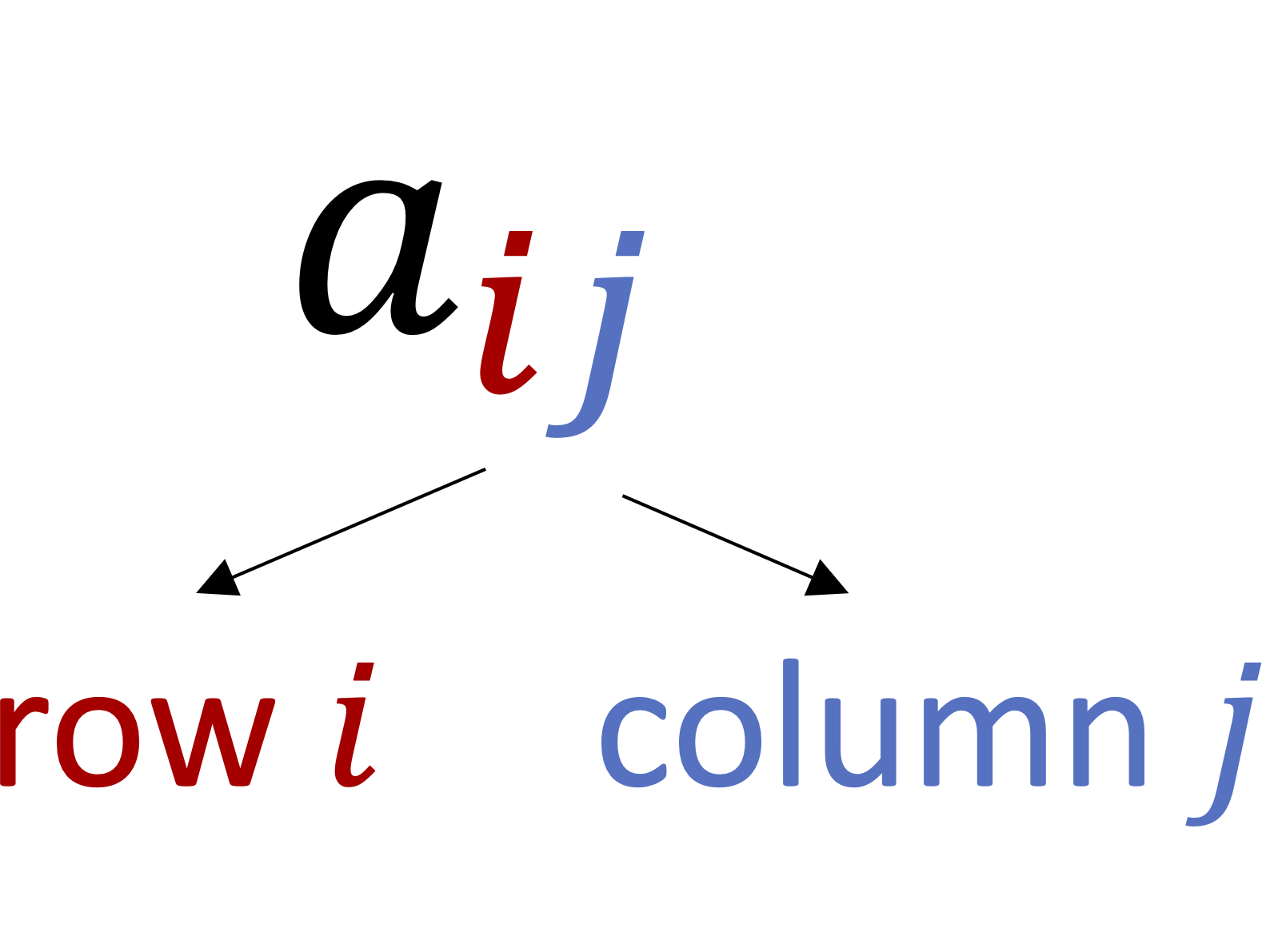
Example 1.1.3. Identifying matrix elements.
For
we have
Checkpoint 1.1.4. Matrix elements.
-
\(a_{3 1} =\)
-
\(a_{4 3} =\)
-
\(a_{1 2} =\)
-
\(a_{2 2} =\)
-
\(a_{4 1} =\)
Subsubsection 1.1.1.3 Matrix equality
Two matrices are equal when they have the same numbers in corresponding entries.
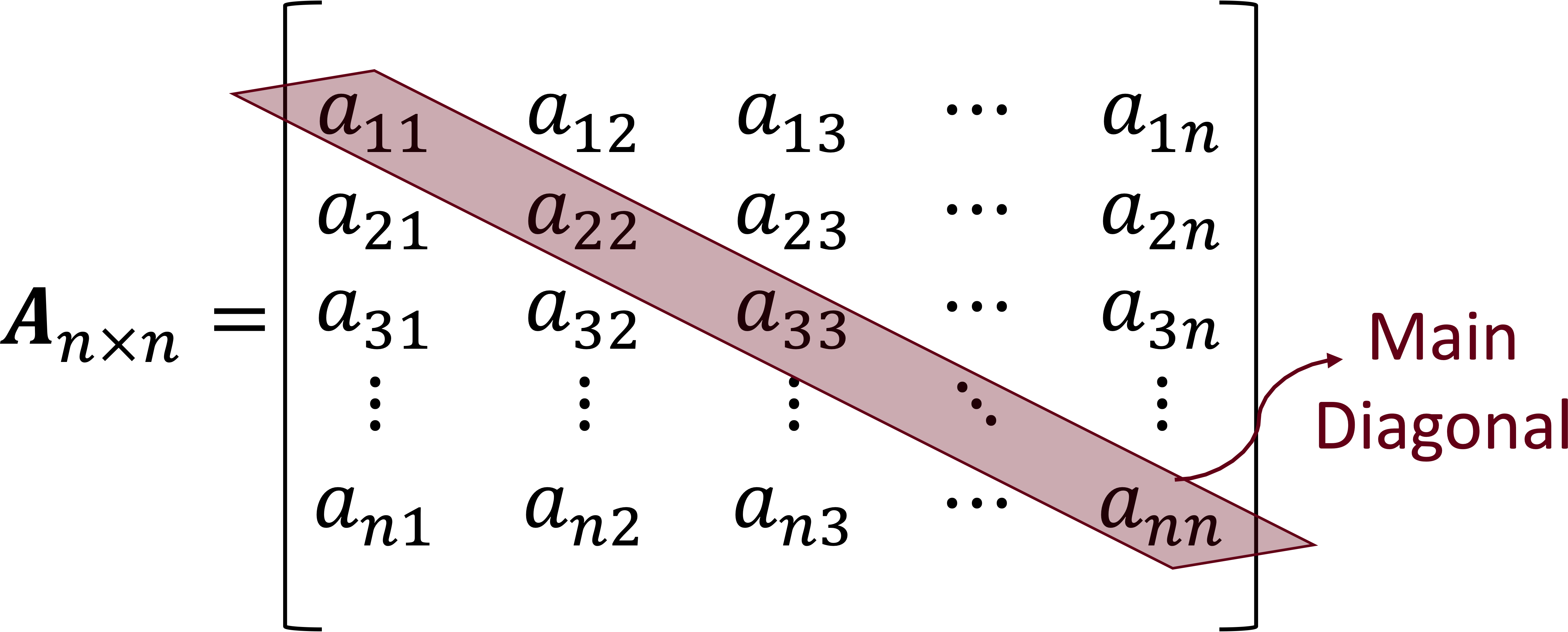
Subsubsection 1.1.1.4 Square matrix
A square matrix has the same number of rows and columns, \(m=n. \) The elements of a square matrix \(\boldsymbol{A}_{n\times n} \) where the subscripts are equal \(\left( a_{11}, a_{22}, \cdots, a_{nn}\right) \) are called the matrix main diagonal.
Subsubsection 1.1.1.5 Identity matrix
An identity matrix is a square matrix with ones in its main diagonal and zeros everywhere else. We use the notation \(\boldsymbol{I}_n \) to indicate an identity matrix that is \(n \times n. \)
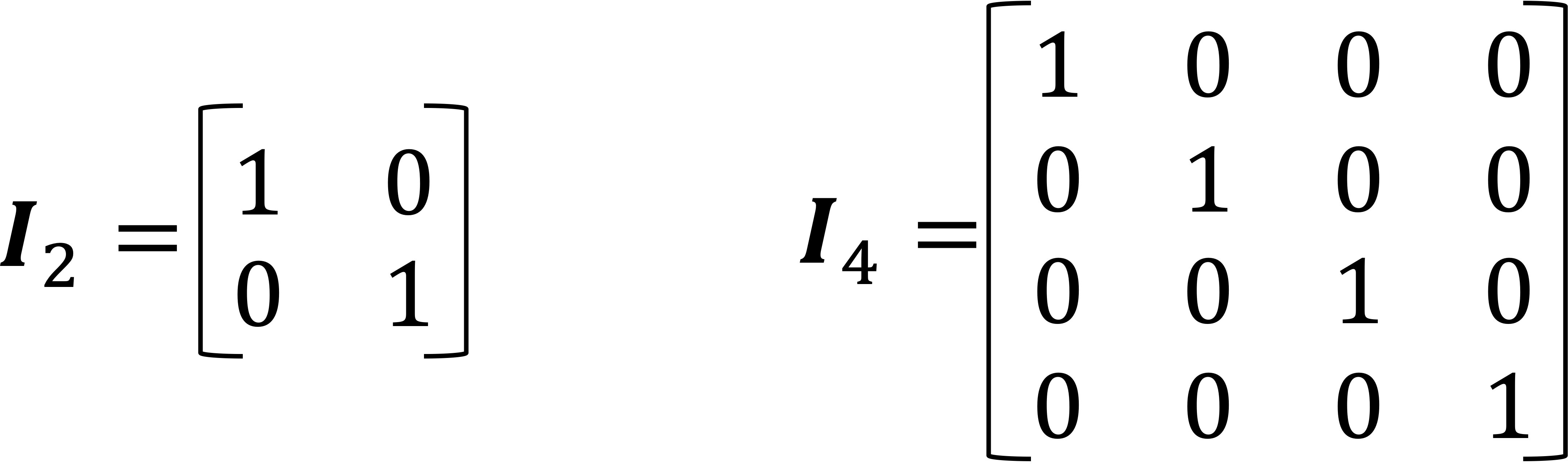
Subsubsection 1.1.1.6 Zero matrix
A zero matrix is a matrix filled with all zeros and denoted by \(\boldsymbol{0}_{m\times n}. \)
Subsection 1.1.2 Matrix operations
Subsubsection 1.1.2.1 Matrix addition
Let \(\boldsymbol{A}_{m\times n} \) and \(\boldsymbol{B}_{m\times n} \) be two matrices of the same size. The sum \(\boldsymbol{C}_{m\times n} = \boldsymbol{A} + \boldsymbol{B} \) is obtained by adding the corresponding elements of \(\boldsymbol{A} \) and \(\boldsymbol{B}: \) \(c_{ij} = a_{ij} + b_{ij}. \) If \(\boldsymbol{A} \) and \(\boldsymbol{B} \) are not the same size the sum does not exists.
Example 1.1.5. Adding matrices.
Let
Find \(\boldsymbol{A}+\boldsymbol{B} \text{.}\)
Checkpoint 1.1.6. Determining if addition exists.
Consider the matrices \(\boldsymbol{A}_{{3}\times {4}}\text{,}\) \(\boldsymbol{B}_{{4}\times {3}}\text{,}\) \(\boldsymbol{C}_{{3}\times {4}}\text{,}\) and \(\boldsymbol{D}_{{6}\times {4}}\text{.}\)
Determine if the following operations exist
-
\(\boldsymbol{A} + \boldsymbol{B}\)
-
Yes
-
No
-
-
\(\boldsymbol{A} + \boldsymbol{C}\)
-
Yes
-
No
-
-
\(\boldsymbol{B} + \boldsymbol{C}\)
-
Yes
-
No
-
-
\(\boldsymbol{C} + \boldsymbol{D}\)
-
Yes
-
No
-
Checkpoint 1.1.7. Adding matrices.
Find \(\boldsymbol{A} + \boldsymbol{B}\) where
| \(\,\) | \(\lceil\) | \(\rceil\) | |||
| \(\boldsymbol{A} + \boldsymbol{B} =\) | \(\lfloor\) | \(\rfloor\) | |||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
\(4\)
\(-4\)
\(-9\)
\(1\)
\(1\)
\(1\)
\(\,\)
Subsubsection 1.1.2.2 Matrix-scalar multiplication
Let \(\boldsymbol{A}_{m \times n} \) be a matrix and \(c\) a scalar. The scalar multiple of \(\boldsymbol{A}\) by \(c\text{,}\) denoted \(c\boldsymbol{A}\text{,}\) is the \(m \times n\) matrix obtained by multiplying every element of \(\boldsymbol{A}\) by \(c\text{,}\) \(\boldsymbol{B} = c\boldsymbol{A} \Rightarrow b_{ij} = c \cdot a_{ij}.\)
Example 1.1.8. Scalar multiplication.
Let
find \(3 \, \boldsymbol{A}.\)
Checkpoint 1.1.9. Multiply a matrix by a scalar.
Find \({3} \boldsymbol{A}\) where
| \(\,\) | \(\lceil\) | \(\rceil\) | ||
| \({3} \boldsymbol{A} =\) | \(\vert\) | \(\vert\) | ||
| \(\,\) | \(\lfloor\) | \(\rfloor\) | ||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
\(3\)
\(-6\)
\(21\)
\(18\)
\(18\)
\(-6\)
Checkpoint 1.1.10. Matrix subtraction.
Let
Find \(\boldsymbol{A} - \boldsymbol{B} \text{.}\)
This is accomplished by combining the addition and scalar multiplication operations introduced in this section.
Finding \(\boldsymbol{A} - \boldsymbol{B}\) is equivalent at finding \(\boldsymbol{A} + ((-1) \cdot \boldsymbol{B}).\) That is, we first multiply \(\boldsymbol{B}\) by \(-1\) and then add this new matrix to \(\boldsymbol{A}.\) Use this procedure to find \(\boldsymbol{A} - \boldsymbol{B} \text{.}\)
| \(\,\) | \(\lceil\) | \(\rceil\) | ||
| \(\boldsymbol{A} - \boldsymbol{B} =\) | \(\lfloor\) | \(\rfloor\) | ||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
\(-4\)
\(-17\)
\(-12\)
\(2\)
\(\,\)
Subsubsection 1.1.2.3 Matrix-matrix multiplication
The matrix product of the matrix \(\boldsymbol{A}_{m \times n} \) and the matrix \(\boldsymbol{B}_{n \times r}, \) is the matrix \(\boldsymbol{C}_{m \times r} = \boldsymbol{A}_{m \times n} \times \boldsymbol{B}_{n \times r},\) where
That is, the \(ij \) element of the product results from multiplying the \(i^{th}\) row of the first matrix with the \(j^{th}\) column of the second matrix and adding the entries.
Example 1.1.11. Matrix multiplication.
Let \(\boldsymbol{A} \) and \(\boldsymbol{B} \) be the two matrix given below. Find \(\boldsymbol{C} = \boldsymbol{A} \times \boldsymbol{B}.\)
- Element \(c_{11} \text{:}\) Row 1
of \(\boldsymbol{A} \) and column 1 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 0 \\ 2 \\ -1 \\ 2 \\ \end{array}\right] \amp = \amp (3) \times (0) \amp + \amp (-2) \times (2) \amp + \amp (4) \times (-1) \amp + \amp (2) \times (2)\\ \amp = \amp 0 \amp - \amp 4 \amp - \amp 4 \amp + \amp 4 \\ \amp = \amp -4 \end{array} \end{equation*}
- Element \(c_{12} \text{:}\) Row 1
of \(\boldsymbol{A} \) and column 2 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 1 \\ -3 \\ 3 \\ 0 \\ \end{array}\right] \amp = \amp (3) \times (1) \amp + \amp (-2) \times (-3) \amp + \amp (4) \times (3) \amp + \amp (2) \times (0)\\ \amp = \amp 3 \amp + \amp 6 \amp + \amp 12 \amp + \amp 0 \\ \amp = \amp 21 \end{array} \end{equation*}
- Element \(c_{13} \text{:}\) Row 1
of \(\boldsymbol{A} \) and column 3 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 3 \amp -2 \amp 4 \amp 2 \\ \end{array}\right] \times \left[ \begin{array}{c} 3 \\ -1 \\ 4 \\ 1 \\ \end{array}\right] \amp = \amp (3) \times (3) \amp + \amp (-2) \times (-1) \amp + \amp (4) \times (4) \amp + \amp (2) \times (1)\\ \amp = \amp 9 \amp + \amp 2 \amp + \amp 16 \amp + \amp 2 \\ \amp = \amp 29 \end{array} \end{equation*}
- Element \(c_{21} \text{:}\) Row 2
of \(\boldsymbol{A} \) and column 1 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 0 \\ 2 \\ -1 \\ 2 \\ \end{array}\right] \amp = \amp (1) \times (0) \amp + \amp (3) \times (2) \amp + \amp (-5) \times (-1) \amp + \amp (-2) \times (2)\\ \amp = \amp 0 \amp + \amp 6 \amp + \amp 5 \amp - \amp 4 \\ \amp = \amp 7 \end{array} \end{equation*}
- Element \(c_{22} \text{:}\) Row 2
of \(\boldsymbol{A} \) and column 2 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 1 \\ -3 \\ 3 \\ 0 \\ \end{array}\right] \amp = \amp (1) \times (1) \amp + \amp (3) \times (-3) \amp + \amp (-5) \times (3) \amp + \amp (-2) \times (0)\\ \amp = \amp 1 \amp - \amp 9 \amp - \amp 15 \amp + \amp 0 \\ \amp = \amp -23 \end{array} \end{equation*}
- Element \(c_{23} \text{:}\) Row 2
of \(\boldsymbol{A} \) and column 3 of
\(\boldsymbol{B}, \)
\begin{equation*} \begin{array}{ccccccccc} \left[ \begin{array}{cccc} 1 \amp 3 \amp -5 \amp -2 \\ \end{array}\right] \times \left[ \begin{array}{c} 3 \\ -1 \\ 4 \\ 1 \\ \end{array}\right] \amp = \amp (1) \times (3) \amp + \amp (3) \times (-1) \amp + \amp (-5) \times (4) \amp + \amp (-2) \times (1)\\ \amp = \amp 3 \amp - \amp 3 \amp - \amp 20 \amp - \amp 2 \\ \amp = \amp -22 \end{array} \end{equation*}
Checkpoint 1.1.12. Multiply two matrices.
Find the product of the two given matrices
| \(\,\) | \(\lceil\) | \(\rceil\) | |||
| \(C =\) | \(\vert\) | \(\vert\) | |||
| \(\,\) | \(\vert\) | \(\vert\) | |||
| \(\,\) | \(\lfloor\) | \(\rfloor\) | |||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
\(-13\)
\(-4\)
\(-9\)
\(6\)
\(1\)
\(-6\)
\(-2\)
\(-1\)
\(-6\)
\(13\)
\(4\)
\(9\)
Insight 1.1.13. Size matters.
In general, not every matrix can be multiplied to any other matrix. Consider the example depicted in the figure below,
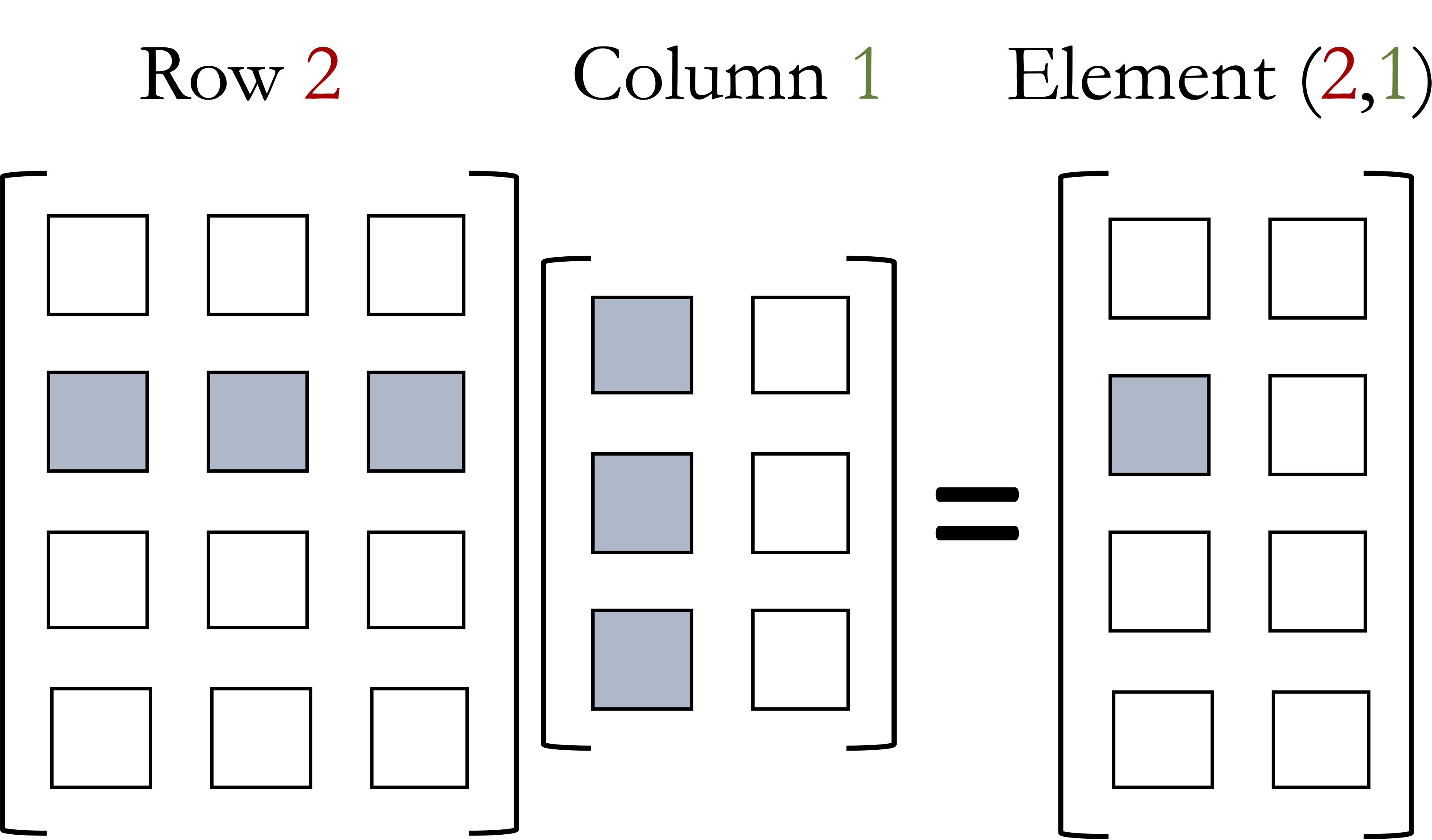
If, for instance, the second matrix had 2 rows instead of 3, the operation will be incomplete.
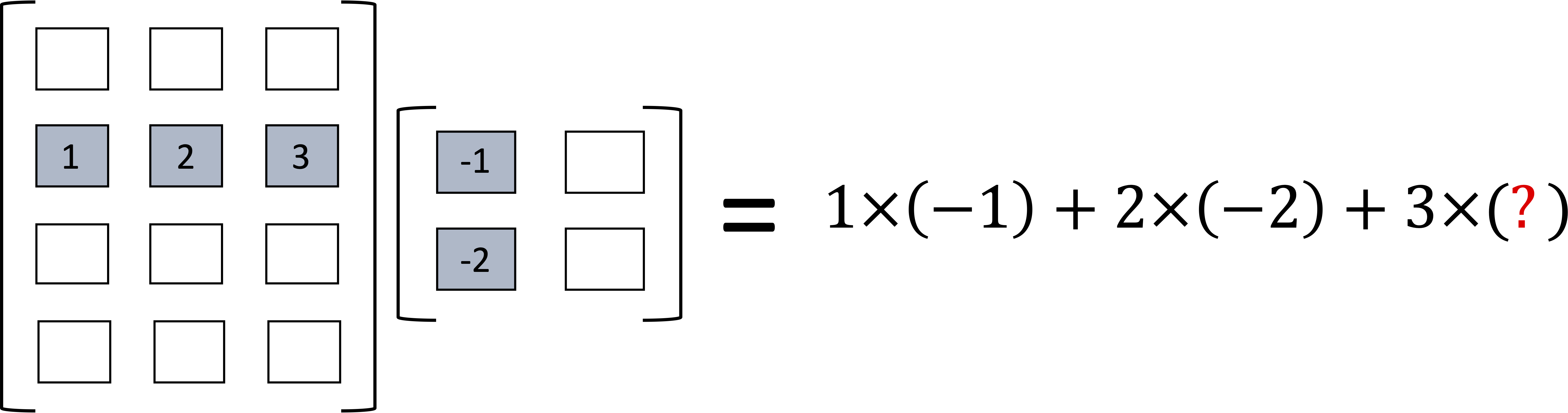
For this reason, we can only multiply matrices that have the "right dimensions." The number of columns in the first matrix has to be the same as the number of rows in the second matrix.
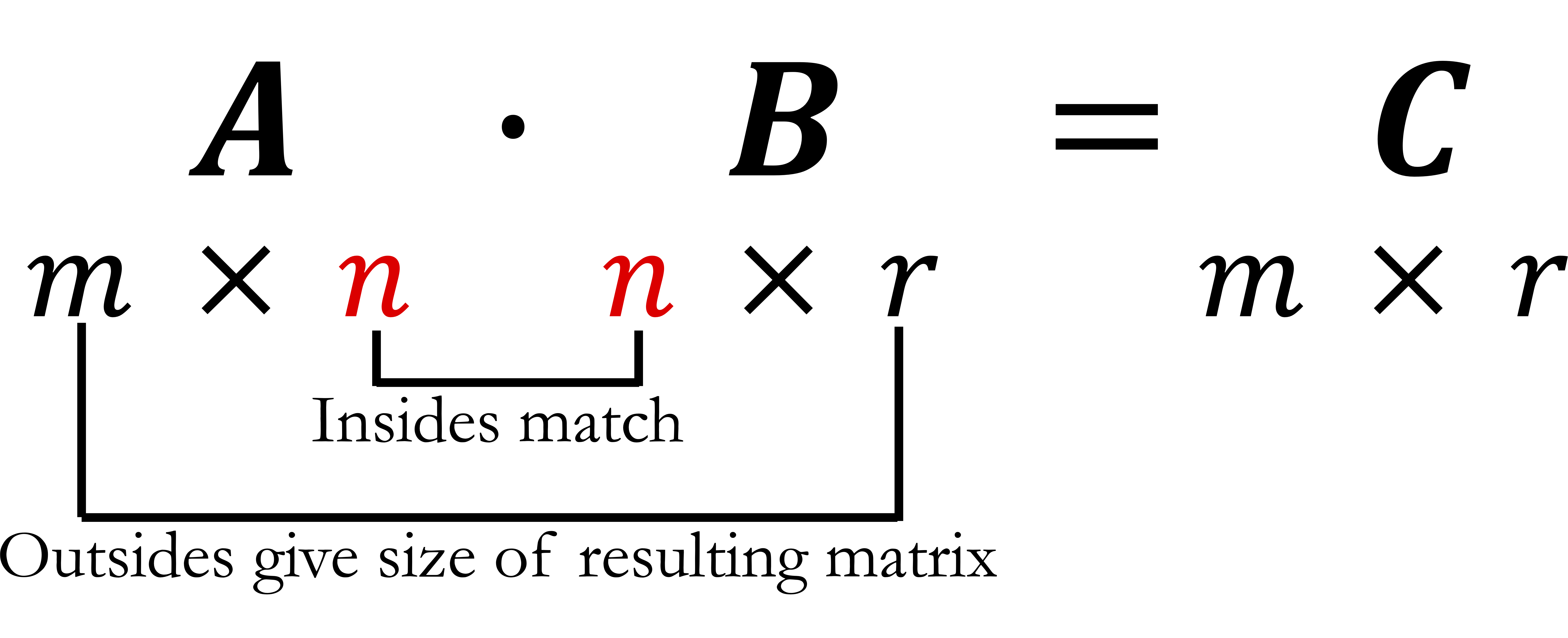
Checkpoint 1.1.14. Matrix multiplication and dimensions.
Determine determine whether the given multiplication is possible. If possible, give the size of the resulting matrix, if not possible write NA.
-
\(\boldsymbol{A}_{{3} \times {3}} \cdot \boldsymbol{B}_{{8} \times {8}}\)
-
Yes
-
No
\(\times\)
-
-
\(\boldsymbol{A}_{{8} \times {1}} \cdot \boldsymbol{B}_{{1} \times {9}}\)
-
Yes
-
No
\(\times\)
-
-
\(\boldsymbol{A}_{{9} \times {3}} \cdot \boldsymbol{B}_{{3} \times {8}}\)
-
Yes
-
No
\(\times\)
-
-
\(\boldsymbol{A}_{{1} \times {9}} \cdot \boldsymbol{B}_{{8} \times {3}}\)
-
Yes
-
No
\(\times\)
-
-
\(\boldsymbol{A}_{{3} \times {8}} \cdot \boldsymbol{B}_{{1} \times {8}}\)
-
Yes
-
No
\(\times\)
-
-
\(\boldsymbol{A}_{{8} \times {1}} \cdot \boldsymbol{B}_{{1} \times {8}}\)
-
Yes
-
No
\(\times\)
-
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{Yes}\)
\(8\)
\(9\)
\(\text{Yes}\)
\(9\)
\(8\)
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{No}\)
\(\text{NA}\)
\(\text{NA}\)
\(\text{Yes}\)
\(8\)
\(8\)
Subsection 1.1.3 Algebraic properties of matrix operations
Subsubsection 1.1.3.1 Properties of matrix sum
For the properties shown below, \(\boldsymbol{A}_{m\times n}, \boldsymbol{B}_{m\times n}, \text{ and } \boldsymbol{C}_{m\times n} \) are matrices and \(r \text{ and } s \) are scalars.
-
Commutative property.
The sum of two matrices is commutative:\begin{equation*} \boldsymbol{A}_{m\times n} + \boldsymbol{B}_{m\times n} = \boldsymbol{B}_{m\times n} + \boldsymbol{A}_{m\times n} \end{equation*}Example 1.1.15. Commutative property.
\begin{equation*} \boldsymbol{A} = \left[ \begin{array}{ccc} 4 \amp 3 \amp 1\\ -1 \amp 0 \amp -2\\ \end{array} \right], \hspace{1cm} \boldsymbol{B} = \left[ \begin{array}{ccc} 2 \amp 0 \amp -1\\ 3 \amp 5 \amp -1\\ \end{array} \right]. \end{equation*}\begin{equation*} \boldsymbol{A}+ \boldsymbol{B} = \left[ \begin{array}{ccc} 4 \amp 3 \amp 1\\ -1 \amp 0 \amp -2\\ \end{array} \right] \hspace{0.2cm} + \hspace{0.2cm} \left[ \begin{array}{ccc} 2 \amp 0 \amp -1\\ 3 \amp 5 \amp -1\\ \end{array} \right] \hspace{0.5cm} = \hspace{0.5cm} \left[ \begin{array}{ccc} 6 \amp 3 \amp 0\\ 2 \amp 5 \amp -3\\ \end{array} \right]. \end{equation*}\begin{equation*} \boldsymbol{B}+ \boldsymbol{A} = \left[ \begin{array}{ccc} 2 \amp 0 \amp -1\\ 3 \amp 5 \amp -1\\ \end{array} \right] \hspace{0.2cm} + \hspace{0.2cm} \left[ \begin{array}{ccc} 4 \amp 3 \amp 1\\ -1 \amp 0 \amp -2\\ \end{array} \right] \hspace{0.5cm} = \hspace{0.5cm} \left[ \begin{array}{ccc} 6 \amp 3 \amp 0\\ 2 \amp 5 \amp -3\\ \end{array} \right]. \end{equation*} -
Associative property.
Matrix addition is associative :\begin{equation*} \boldsymbol{A}_{m\times n} + \left( \boldsymbol{B}_{m\times n} + \boldsymbol{C}_{m\times n} \right) = \left(\boldsymbol{A}_{m\times n} + \boldsymbol{B}_{m\times n}\right) + \boldsymbol{C}_{m\times n}. \end{equation*}Example 1.1.16. Associative property.
If we have more than two matrices to add, we can first sum two of them and then add the third matrix to this result. This property tell us that the order in which we choose the first two matrices does not matter.
Consider the following three matrices
\begin{equation*} \boldsymbol{A} = \left[ \begin{array}{cc} 2 \amp 1 \\ 0 \amp 3\\ \end{array}\right], \hspace{1cm} \boldsymbol{B} = \left[ \begin{array}{cc} -1 \amp 0 \\ 1 \amp 2\\ \end{array}\right], \hspace{1cm} \boldsymbol{C} = \left[ \begin{array}{cc} 0 \amp -4 \\ 1 \amp -2\\ \end{array}\right]. \end{equation*}-
Note that \(\boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} \) can be obtained by first adding \(\boldsymbol{A} \) and \(\boldsymbol{B}\) and then adding the resulting matrix to \(\boldsymbol{C}: \)
\begin{equation*} \boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} = \left(\boldsymbol{A} + \boldsymbol{B}\right) + \boldsymbol{C}. \end{equation*}\begin{equation*} \left(\boldsymbol{A} + \boldsymbol{B}\right) = \left[ \begin{array}{cc} 2 \amp 1 \\ 0 \amp 3\\ \end{array}\right] + \left[ \begin{array}{cc} -1 \amp 0 \\ 1 \amp 2\\ \end{array}\right] = \left[ \begin{array}{cc} 1 \amp 1 \\ 1 \amp 5\\ \end{array}\right] \end{equation*}\begin{equation*} \left(\boldsymbol{A} + \boldsymbol{B}\right) + \boldsymbol{C} = \left[ \begin{array}{cc} 1 \amp 1 \\ 1 \amp 5\\ \end{array}\right] + \left[ \begin{array}{cc} 0 \amp -4 \\ 1 \amp -2\\ \end{array}\right]= \left[ \begin{array}{cc} 1 \amp -3 \\ 2 \amp 3\\ \end{array}\right]. \end{equation*} -
Alternatively, \(\boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} \) can be obtained by first adding \(\boldsymbol{B} \) and \(\boldsymbol{C}\) and then adding the resulting matrix to \(\boldsymbol{A}: \)
\begin{equation*} \boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} = \boldsymbol{A} + \left(\boldsymbol{B} + \boldsymbol{C}\right). \end{equation*}\begin{equation*} \left(\boldsymbol{B} + \boldsymbol{C}\right) = \left[ \begin{array}{cc} -1 \amp 0 \\ 1 \amp 2\\ \end{array}\right] + \left[ \begin{array}{cc} 0 \amp -4 \\ 1 \amp -2\\ \end{array}\right] = \left[ \begin{array}{cc} -1 \amp -4 \\ 2 \amp 0\\ \end{array}\right] \end{equation*}\begin{equation*} \boldsymbol{A} + \left(\boldsymbol{B}+ \boldsymbol{C} \right) = \left[ \begin{array}{cc} 2 \amp 1 \\ 0 \amp 3\\ \end{array}\right] + \left[ \begin{array}{cc} -1 \amp -4 \\ 2 \amp 0\\ \end{array}\right]= \left[ \begin{array}{cc} 1 \amp -3 \\ 2 \amp 3\\ \end{array}\right]. \end{equation*} -
Another alternative is to find \(\boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} \) by first adding \(\boldsymbol{A} \) and \(\boldsymbol{C}\) and then adding the resulting matrix to \(\boldsymbol{B}: \)
\begin{equation*} \boldsymbol{A} + \boldsymbol{B} + \boldsymbol{C} = \left( \boldsymbol{A} + \boldsymbol{C}\right) + \boldsymbol{B}. \end{equation*}\begin{equation*} \left(\boldsymbol{A} + \boldsymbol{C}\right) = \left[ \begin{array}{cc} 2 \amp 1 \\ 0 \amp 3\\ \end{array}\right] + \left[ \begin{array}{cc} 0 \amp -4 \\ 1 \amp -2\\ \end{array}\right] = \left[ \begin{array}{cc} 2 \amp -3 \\ 1 \amp 1\\ \end{array}\right] \end{equation*}\begin{equation*} \left(\boldsymbol{A} + \boldsymbol{C} \right)+ \boldsymbol{B} = \left[ \begin{array}{cc} 2 \amp -3 \\ 1 \amp 1\\ \end{array}\right] + \left[ \begin{array}{cc} -1 \amp 0 \\ 1 \amp 2\\ \end{array}\right]= \left[ \begin{array}{cc} 1 \amp -3 \\ 2 \amp 3\\ \end{array}\right]. \end{equation*}
-
Subsubsection 1.1.3.2 Properties of matrix-scalar multiplication
For the properties shown below, \(\boldsymbol{A}_{m\times n}, \boldsymbol{B}_{m\times n}, \text{ and } \boldsymbol{C}_{m\times n} \) are matrices and \(r \text{ and } s \) are scalars.
-
Distributive property 1.
Multiplication of a matrix by a scalar is distributive with respect to matrix addition:\begin{equation*} r \left( \boldsymbol{A}_{m\times n} + \boldsymbol{B}_{m\times n}\right) = r\, \boldsymbol{A}_{m\times n} + r\, \boldsymbol{B}_{m\times n}. \end{equation*}Example 1.1.17. Distributive property 1.
\begin{equation*} \begin{array}{ccc} 4 \times \left( \left[ \begin{array}{rr} -1 \amp 2 \\ 0 \amp 4 \\ 1 \amp 3 \\ -2 \amp 1 \\ \end{array}\right] + \left[ \begin{array}{rr} 3 \amp -1 \\ 1 \amp 1 \\ 2 \amp -4 \\ -2 \amp 2 \\ \end{array}\right] \right) \amp = \amp 4 \times \left[ \begin{array}{rr} -1 \amp 2 \\ 0 \amp 4 \\ 1 \amp 3 \\ -2 \amp 1 \\ \end{array}\right] + 4 \times \left[ \begin{array}{rr} 3 \amp -1 \\ 1 \amp 1 \\ 2 \amp -4 \\ -2 \amp 2 \\ \end{array}\right] \\ \end{array} \end{equation*}\begin{equation*} \hspace{1.5cm} \begin{array}{ccc} 4 \times \left( \left[ \begin{array}{rr} 2 \amp 1 \\ 1 \amp 5 \\ 3 \amp -1 \\ -4 \amp 3 \\ \end{array}\right] \right) \amp \hspace{0.9cm} = \hspace{0.9cm} \amp \left[ \begin{array}{rr} -4 \amp 8 \\ 0 \amp 16 \\ 4 \amp 12 \\ -8 \amp 4 \\ \end{array}\right] + \left[ \begin{array}{rr} 12 \amp -4 \\ 4 \amp 4 \\ 8 \amp -16 \\ -8 \amp 8 \\ \end{array}\right] \\ \amp \amp\\ \left[ \begin{array}{rr} 8 \amp 4 \\ 4 \amp 20 \\ 12 \amp -4 \\ -16 \amp 12 \\ \end{array}\right] \amp \hspace{0.9cm} = \hspace{0.9cm} \amp \left[ \begin{array}{rr} 8 \amp 4 \\ 4 \amp 20 \\ 12 \amp -4 \\ -16 \amp 12 \\ \end{array}\right] \\ \end{array} \end{equation*} -
Distributive property 2.
Multiplication of a matrix by a scalar is distributive with respect to the scalar addition:\begin{equation*} \left(r+s \right) \boldsymbol{C}_{m\times n} = r\, \boldsymbol{C}_{m\times n} + s\, \boldsymbol{C}_{m\times n}. \end{equation*}Example 1.1.18. Distributive property 2.
\begin{equation*} \begin{array}{l} (2 + 4) \times \left[\begin{array}{rr} -2 \amp 1 \\ 0 \amp 1 \\ \end{array}\right] = 2 \times \left[\begin{array}{rr} -2 \amp 1 \\ 0 \amp 1 \\ \end{array}\right] + 4 \times \left[\begin{array}{rr} -2 \amp 1 \\ 0 \amp 1 \\ \end{array}\right]\\ \amp \amp \\ \hspace{0.7cm} 6 \times \left[\begin{array}{rr} -2 \amp 1 \\ 0 \amp 1 \\ \end{array}\right] \hspace{0.5cm} = \hspace{0.5cm} \left[\begin{array}{rr} -4 \amp 2 \\ 0 \amp 2 \\ \end{array}\right] \hspace{0.3cm} + \hspace{0.3cm} \left[\begin{array}{rr} -8 \amp 4 \\ 0 \amp 4 \\ \end{array}\right]\\ \amp \amp \\ \hspace{0.7cm}\left[\begin{array}{rr} -12 \amp 6 \\ 0 \amp 6 \\ \end{array}\right] \hspace{1.1cm} = \hspace{1.5cm} \left[\begin{array}{rr} -12 \amp 6 \\ 0 \amp 6 \\ \end{array}\right] \\ \end{array} \end{equation*} -
Associative property.
Multiplication of a matrix by a scalar is associative with respect to the scalar multiplication:\begin{equation*} r \left(s \times \boldsymbol{C}_{m\times n} \right) = (r\, s) \boldsymbol{C}_{m\times n}. \end{equation*}Example 1.1.19. Associative property.
\begin{equation*} \begin{array}{l} -1 \times \left( 2\times \left[\begin{array}{rrr} 1 \amp -1 \amp 3 \\ 2 \amp 0 \amp -1 \\ 3 \amp 0 \amp 0\\ \end{array}\right] \right) = (-1 \times 2 ) \times \left[\begin{array}{rrr} 1 \amp -1 \amp 3 \\ 2 \amp 0 \amp -1 \\ 3 \amp 0 \amp 0\\ \end{array}\right] \\ \amp \amp \\ \hspace{0.7cm} -1 \times \left[\begin{array}{rrr} 2 \amp -2 \amp 6 \\ 4 \amp 0 \amp -2 \\ 6 \amp 0 \amp 0\\ \end{array}\right] \hspace{0.9cm} = \hspace{0.9cm} -2 \times \left[\begin{array}{rrr} 1 \amp -1 \amp 3 \\ 2 \amp 0 \amp -1 \\ 3 \amp 0 \amp 0\\ \end{array}\right]\\ \amp \amp \\ \hspace{1.1cm}\left[\begin{array}{rrr} -2 \amp 2 \amp -6 \\ -4 \amp 0 \amp 2 \\ -6 \amp 0 \amp 0\\ \end{array}\right] \hspace{1.6cm} = \hspace{1cm} \left[\begin{array}{rrr} -2 \amp 2 \amp -6 \\ -4 \amp 0 \amp 2 \\ -6 \amp 0 \amp 0\\ \end{array}\right] \\ \end{array} \end{equation*}
Subsubsection 1.1.3.3 Properties of matrix-matrix multiplication
For the properties shown below, \(\boldsymbol{A}, \boldsymbol{B}, \text{ and } \boldsymbol{C} \) are matrices and \(r \) is a scalar. The sizes for the matrices will be given for each property.
-
Associative property.
Matrix-matrix multiplication is associative:\begin{equation*} \begin{array}{ccc} \boldsymbol{A} \left(\boldsymbol{B}\,\boldsymbol{C}\right) \amp = \amp \left(\boldsymbol{A}\,\boldsymbol{B}\right)\,\boldsymbol{C}\\ \amp \amp \\ \boldsymbol{A}_{m\times n} \left(\boldsymbol{B}_{n\times p} \boldsymbol{C}_{p\times q}\right) \amp = \amp \left(\boldsymbol{A}_{m\times n} \boldsymbol{B}_{n\times p}\right) \boldsymbol{C}_{p\times q}.\\ \end{array} \end{equation*}Example 1.1.20. Associative property.
\begin{equation*} \begin{array}{ccc} \boldsymbol{A}_{3\times 2} \left(\boldsymbol{B}_{2\times 4} \boldsymbol{C}_{4\times 3}\right) \amp = \amp \left(\boldsymbol{A}_{3\times 2} \boldsymbol{B}_{2\times 4}\right) \boldsymbol{C}_{4\times 3}\\ \amp \amp \\ \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \left( \left[ \begin{array}{rrrr} 0 \amp 1 \amp -1 \amp 3\\ 2 \amp -1 \amp 1 \amp -2\\ \end{array}\right]\, \left[ \begin{array}{rrr} 1 \amp -1 \amp -3\\ 2 \amp 3 \amp 1 \\ 4 \amp 1 \amp 0 \\ 0 \amp -2 \amp 1 \\ \end{array}\right] \right) \amp = \amp \left( \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right] \, \left[ \begin{array}{rrrr} 0 \amp 1 \amp -1 \amp 3\\ 2 \amp -1 \amp 1 \amp -2\\ \end{array}\right] \right)\, \left[ \begin{array}{rrr} 1 \amp -1 \amp -3\\ 2 \amp 3 \amp 1 \\ 4 \amp 1 \amp 0 \\ 0 \amp -2 \amp 1 \\ \end{array}\right] \end{array} \end{equation*}\begin{equation*} \begin{array}{lll} \hspace{2cm} \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \left[ \begin{array}{rrr} -6 \amp -5 \amp 4 \\ 4 \amp 0 \amp -9 \\ \end{array}\right] \hspace{2.8cm} \amp = \amp \hspace{1.7cm} \left[ \begin{array}{rrrr} 2 \amp 0 \amp -1 \amp 1 \\ 0 \amp -2 \amp 4 \amp -6 \\ 2 \amp 2 \amp -5 \amp 7 \\ \end{array}\right]\, \left[ \begin{array}{rrr} 1 \amp -1 \amp -3\\ 2 \amp 3 \amp 1 \\ 4 \amp 1 \amp 0 \\ 0 \amp -2 \amp 1 \\ \end{array}\right]\\ \amp \amp \\ \hspace{2.2cm} \left[ \begin{array}{rrr} -2 \amp -5 \amp -5 \\ 12 \amp 10 \amp -8 \\ -14 \amp -15 \amp 3 \\ \end{array}\right]_{3 \times 3} \amp = \amp \hspace{2.2cm} \left[ \begin{array}{rrr} -2 \amp -5 \amp -5 \\ 12 \amp 10 \amp -8 \\ -14 \amp -15 \amp 3 \\ \end{array}\right]_{3 \times 3} \end{array} \end{equation*} -
Distributive property.
Matrix-matrix multiplication is distributive with respect to matrix addition:
-
Case 1:
\begin{equation*} \begin{array}{ccc} \boldsymbol{A}\,\left(\boldsymbol{B} + \boldsymbol{C} \right) \amp = \amp \boldsymbol{A}\,\boldsymbol{B} + \boldsymbol{A}\,\boldsymbol{C} \amp \amp\\ \boldsymbol{A}_{m\times n}\,\left(\boldsymbol{B}_{n\times p} + \boldsymbol{C}_{n\times p} \right) \amp = \amp \boldsymbol{A}_{m\times n}\,\boldsymbol{B}_{n\times p} + \boldsymbol{A}_{m\times n}\,\boldsymbol{C}_{n\times p} \end{array} \end{equation*}Example 1.1.21. Distributive property - Case 1.
\begin{equation*} \begin{array}{ccc} \boldsymbol{A}_{3\times 2}\,\left(\boldsymbol{B}_{2\times 4} + \boldsymbol{C}_{2\times 4}\right) \amp = \amp \boldsymbol{A}_{3\times 2}\,\boldsymbol{B}_{2\times 4} + \boldsymbol{A}_{3\times 2}\,\boldsymbol{C}_{2\times 4}\\ \amp \amp \\ \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \left( \left[ \begin{array}{rrrr} 0 \amp 1 \amp -1 \amp 3\\ 2 \amp -1 \amp 1 \amp -2\\ \end{array}\right] + \left[ \begin{array}{rrrr} 1 \amp -1 \amp -3 \amp 1\\ 2 \amp 3 \amp 1 \amp 0 \\ \end{array}\right] \right) \amp = \amp \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \left[ \begin{array}{rrrr} 0 \amp 1 \amp -1 \amp 3\\ 2 \amp -1 \amp 1 \amp -2\\ \end{array}\right] + \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \left[ \begin{array}{rrrr} 1 \amp -1 \amp -3 \amp 1\\ 2 \amp 3 \amp 1 \amp 0 \\ \end{array}\right] \end{array} \end{equation*}\begin{equation*} \begin{array}{lll} \left[ \begin{array}{rr} 1 \amp 1\\ -2 \amp 0 \\ 3 \amp 1\\ \end{array}\right]\, \hspace{1cm} \left[ \begin{array}{rrrr} 1 \amp 0 \amp-4 \amp 4\\ 4 \amp 2 \amp 2 \amp -2\\ \end{array}\right] \hspace{4.3cm} \amp = \amp \hspace{1cm}\left[ \begin{array}{rrrr} 2 \amp 0 \amp 0 \amp 1\\ 0 \amp -2 \amp 2 \amp -6\\ 2 \amp 2 \amp -2 \amp 7\\ \end{array}\right] \hspace{1cm} + \hspace{0.4cm} \left[ \begin{array}{rrrr} 3 \amp 2 \amp -2 \amp 1\\ -2 \amp 2 \amp 6 \amp -2\\ 5 \amp 0 \amp -8 \amp 3\\ \end{array}\right]\\ \amp \amp\\ \hspace{5cm}\left[ \begin{array}{rrrr} 5 \amp 2 \amp -2 \amp 2\\ -2 \amp 0 \amp 8 \amp -8\\ 7 \amp 2 \amp -10 \amp 10\\ \end{array}\right] \amp = \amp \hspace{2cm}\left[ \begin{array}{rrrr} 5 \amp 2 \amp -2 \amp 2\\ -2 \amp 0 \amp 8 \amp -8\\ 7 \amp 2 \amp -10 \amp 10\\ \end{array}\right] \end{array} \end{equation*} -
Case 2:
\begin{equation*} \begin{array}{ccc} \left( \boldsymbol{A} + \boldsymbol{B}\right)\,\boldsymbol{C} \amp = \amp \boldsymbol{A}\,\boldsymbol{C} + \boldsymbol{B}\,\boldsymbol{C} \amp \amp\\ \left( \boldsymbol{A}_{m\times n} + \boldsymbol{B}_{m\times n}\right)\,\boldsymbol{C}_{n\times p} \amp = \amp \boldsymbol{A}_{m\times n}\,\boldsymbol{C}_{n\times p} + \boldsymbol{B}_{m\times n}\,\boldsymbol{C}_{n\times p} \end{array} \end{equation*}Example 1.1.22. Distributive property - Case 2.
\begin{equation*} \begin{array}{ccc} \left( \boldsymbol{A}_{2\times 2} + \boldsymbol{B}_{2\times 2}\right)\,\boldsymbol{C}_{2\times 3} \amp = \amp \boldsymbol{A}_{2\times 2}\,\boldsymbol{C}_{2\times 3} + \boldsymbol{B}_{2\times 2}\,\boldsymbol{C}_{2\times 3}\\ \amp \amp \\ \left( \left[ \begin{array}{rr} 1 \amp 0\\ 0 \amp 1 \\ \end{array}\right] + \left[ \begin{array}{rr} 3 \amp -2\\ 1 \amp 4 \\ \end{array}\right] \right)\, \left[ \begin{array}{rrr} 2 \amp 1 \amp 0\\ 1 \amp 3 \amp -1 \end{array}\right] \amp = \amp \left[ \begin{array}{rr} 1 \amp 0\\ 0 \amp 1 \\ \end{array}\right]\, \left[ \begin{array}{rrr} 2 \amp 1 \amp 0\\ 1 \amp 3 \amp -1 \end{array}\right] + \left[ \begin{array}{rr} 3 \amp -2\\ 1 \amp 4 \\ \end{array}\right]\, \left[ \begin{array}{rrr} 2 \amp 1 \amp 0\\ 1 \amp 3 \amp -1 \end{array}\right] \end{array} \end{equation*}\begin{equation*} \begin{array}{lll} \hspace{1cm}\left[ \begin{array}{rr} 4 \amp -2\\ 1 \amp 5 \\ \end{array}\right]\, \left[ \begin{array}{rrr} 2 \amp 1 \amp 0\\ 1 \amp 3 \amp -1 \end{array}\right]\hspace{1.5cm} \amp = \amp \hspace{1cm} \left[ \begin{array}{rrr} 2 \amp 1 \amp 0\\ 1 \amp 3 \amp -1 \end{array}\right] + \left[ \begin{array}{rrr} 4 \amp -3 \amp 2\\ 6 \amp 13 \amp -4 \end{array}\right]\\ \amp \amp\\ \hspace{2cm}\left[ \begin{array}{rrr} 6 \amp -2 \amp 2\\ 7 \amp 16 \amp -5 \end{array}\right] \amp = \amp \hspace{2cm}\left[ \begin{array}{rrr} 6 \amp -2 \amp 2\\ 7 \amp 16 \amp -5 \end{array}\right] \end{array} \end{equation*}
-
-
Associative property with scalar multiplication.
Matrix multiplication is associative with respect to scalar multiplication:
\begin{equation*} \begin{array}{cll} r \left(\boldsymbol{A}\,\boldsymbol{B}\right) \amp = \left(r\,\boldsymbol{A}\right)\,\boldsymbol{B} \amp = \boldsymbol{A}\,\left(r\,\boldsymbol{B} \right)\\ \amp \amp\\ r \left(\boldsymbol{A}_{m\times n}\,\boldsymbol{B}_{n\times p}\right) \amp = \left(r\,\boldsymbol{A}\right)_{m\times n}\,\boldsymbol{B}_{n\times p} \amp = \boldsymbol{A}_{m\times n}\,\left(r\,\boldsymbol{B} \right)_{n\times p} \end{array} \end{equation*}Example 1.1.23. Associative property with scalar multiplication.
\begin{equation*} \begin{array}{cll} 2 \left(\boldsymbol{A}_{2\times 2}\,\boldsymbol{B}_{2\times 2}\right) \amp = \left(2\,\boldsymbol{A}\right)_{2\times 2}\,\boldsymbol{B}_{2\times 2} \amp = \boldsymbol{A}_{2\times 2}\,\left(2\,\boldsymbol{B} \right)_{2\times 2} \amp \amp \\ \amp \amp \\ 2 \left( \left[ \begin{array}{rr} 3 \amp 2\\ 1 \amp 0\\ \end{array}\right]\, \left[ \begin{array}{rr} 1 \amp -1\\ 2 \amp 1\\ \end{array}\right] \right) \amp = \left( 2\,\left[ \begin{array}{rr} 3 \amp 2\\ 1 \amp 0\\ \end{array}\right] \right)\, \left[ \begin{array}{rr} 1 \amp -1\\ 2 \amp 1\\ \end{array}\right] \amp = \left[ \begin{array}{rr} 3 \amp 2\\ 1 \amp 0\\ \end{array}\right]\, \left( 2\,\left[ \begin{array}{rr} 1 \amp -1\\ 2 \amp 1\\ \end{array}\right] \right)\\ \amp \amp \\ 2\, \left[ \begin{array}{rr} 7 \amp -1\\ 1 \amp -1\\ \end{array}\right] \amp = \left[ \begin{array}{rr} 6 \amp 4\\ 3 \amp 0\\ \end{array}\right]\, \left[ \begin{array}{rr} 1 \amp -1\\ 2 \amp 1\\ \end{array}\right] \amp = \left[ \begin{array}{rr} 3 \amp 2\\ 1 \amp 0\\ \end{array}\right]\, \left[ \begin{array}{rr} 2 \amp -2\\ 4 \amp 2\\ \end{array}\right]\\ \end{array} \end{equation*}\begin{equation*} \begin{array}{lll} \amp \amp \\ \left[ \begin{array}{rr} 14 \amp -2\\ 2 \amp -2\\ \end{array}\right] \hspace{0.5cm} \amp = \hspace{1cm}\left[ \begin{array}{rr} 14 \amp -2\\ 2 \amp -2\\ \end{array}\right]\hspace{1cm} \amp = \hspace{1cm}\left[ \begin{array}{rr} 14 \amp -2\\ 2 \amp -2\\ \end{array}\right] \end{array} \end{equation*}
Subsection 1.1.4 Non-properties of matrices
Insight 1.1.24. Equal product of two matirices.
Example 1.1.25. Matrix product and equality.
Consider the following three matrices,
and
However, \(\boldsymbol{B} \ne \boldsymbol{C}. \)
Insight 1.1.26. Product of two matrices equal to zero.
Example 1.1.27. Zero product.
Consider the following two matrices,
However, neither \(\boldsymbol{A} \) nor \(\boldsymbol{B} \) are the zero matrix.
Subsection 1.1.5 Powers of matrices
Definition 1.1.28. Power of a matrix.
The \(k\) power of a matrix is defined as
By definition,
where \(\boldsymbol{I} \) denotes the identity matrix (1.1.1.5).
Subsubsection 1.1.5.1 Product of two powers
The following holds for any square matrix \(\boldsymbol{A}_{n \times n} \) and integers \(p \) and \(q\text{,}\)
Example 1.1.29. Product of two powers of matrices.
Consider the matrix,
-
Calculate \(\boldsymbol{A}^2 \)
\begin{equation*} \boldsymbol{A}^2 = \boldsymbol{A} \cdot \boldsymbol{A} = \left[ \begin{array}{cc} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] = \left[ \begin{array}{rr} 0 \amp -1 \\ 1 \amp -1 \\ \end{array} \right]. \end{equation*} -
Calculate \(\boldsymbol{A}^3 \)
\begin{equation*} \begin{array}{ccl} \boldsymbol{A}^3 = \boldsymbol{A} \cdot \boldsymbol{A} \cdot \boldsymbol{A} \amp = \amp \underbrace{\left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \\ \amp = \amp \hspace{1.cm} \underbrace{\left[ \begin{array}{rr} 0 \amp -1 \\ 1 \amp -1 \\ \end{array} \right] \hspace{1.1cm} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]} \\ \amp = \amp \hspace{2.2cm} \left[ \begin{array}{rr} -1 \amp 0 \\ 0 \amp -1 \\ \end{array} \right] \end{array} \end{equation*} -
Calculate \(\boldsymbol{A}^5 \)
\begin{equation*} \begin{array}{ccl} \boldsymbol{A}^5 = \boldsymbol{A} \cdot \boldsymbol{A} \cdot \boldsymbol{A}\cdot \boldsymbol{A} \cdot \boldsymbol{A} \amp =\amp \underbrace{\left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \\ \amp = \amp \hspace{1.cm} \underbrace{\left[ \begin{array}{rr} 0 \amp -1 \\ 1 \amp -1 \\ \end{array} \right] \hspace{1.1cm} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]\\ \end{array} \end{equation*}\begin{equation*} \begin{array}{ccl} \hspace{4.7cm} \amp = \amp \hspace{2.4cm} \underbrace{\left[ \begin{array}{rr} -1 \amp 0 \\ 0 \amp -1 \\ \end{array} \right] \hspace{1.5cm} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]\\ \amp = \amp \hspace{4.4cm} \underbrace{\left[ \begin{array}{rr} -1 \amp 1 \\ -1 \amp 0 \\ \end{array} \right]\hspace{2cm} \cdot \left[ \begin{array}{rr} 1 \amp -1 \\ 1 \amp 0 \\ \end{array} \right]}\\ \amp = \amp \hspace{6.4cm} \left[ \begin{array}{rr} 0 \amp 1 \\ -1 \amp 1 \\ \end{array} \right] \end{array} \end{equation*}Alternatively, instead of multiplying \(\boldsymbol{A} \) 5-times, we can use \(\boldsymbol{A}^2 \) and \(\boldsymbol{A}^3 \) to find \(\boldsymbol{A}^5 \text{,}\)
\begin{equation*} \begin{array}{ccl} \boldsymbol{A}^5 = \boldsymbol{A}^2 \cdot \boldsymbol{A}^3 \amp = \amp \underbrace{\left[ \begin{array}{rr} 0 \amp -1 \\ 1 \amp -1 \\ \end{array} \right] \cdot \left[ \begin{array}{rr} -1 \amp 0 \\ 0 \amp -1 \\ \end{array} \right]}\\ \amp = \amp \hspace{1.3cm} \left[ \begin{array}{rr} 0 \amp 1 \\ -1 \amp 1 \\ \end{array} \right]. \end{array} \end{equation*}
Insight 1.1.30. Size matters - square matrix.
Consider the matrix,
Find \(\boldsymbol{A}^2 \text{.}\)
This is not possible, since we cannot obtain the product,
In general, we cannot obtain powers of a non-square matrix \(\boldsymbol{A} \text{,}\) because we cannot multiply a \(n \times m \) matrix by another \(n \times m \) matrix unless \(n = m \text{.}\)
Subsubsection 1.1.5.2 Power of a power
The following holds for any square matrix \(\boldsymbol{A}_{n \times n} \) and integers \(p \) and \(q\text{,}\)
Example 1.1.31. Product of two powers of matrices.
Consider the matrix,
Find \(\boldsymbol{A}^{10}. \)
From the previous example we know that
We can use this and \(\boldsymbol{A}^{10} = \left(\boldsymbol{A}^5\right)^2 \) to get our solution:
Checkpoint 1.1.32. Find the power of a matrix.
Find \(\boldsymbol{A}^6\) where
| \(\,\) | \(\lceil\) | \(\rceil\) | |||
| \(\boldsymbol{A}^6 =\) | \(\lfloor\) | \(\rfloor\) | |||
| \(\,\) | \(\,\) | \(\,\) | \(\,\) |
\(729\)
\(0\)
\(-364\)
\(1\)
Subsection 1.1.6 Homework
Link to webwork: HW 2.1

