Skip to main content

Section 1.1 Eigenvalues and Eigenvectors

\(\, \)

\(\Large{\textbf{Section Content}} \)

\(\, \)

Subsection 1.1.1 Definition of eigenvalues and eigenvectors

Subsubsection 1.1.1.1 Geometrical meaning

Consider the following matrix,

\begin{equation*} \bA{A} = \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right]. \end{equation*}

Take the following vectors and find the product of each with \(\bA{A}\text{,}\)

\begin{equation*} \begin{array}{ccccc} \bA{b}_1 = \left[\begin{array}{c} 1\\2 \end{array}\right], \amp\amp \bA{b}_2 = \left[\begin{array}{c} -1\\2 \end{array}\right], \amp\amp \bA{b}_3 = \left[\begin{array}{c} 1\\1 \end{array}\right]. \\ \amp\amp\amp\amp\\ \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right]\, \left[\begin{array}{c} 1\\2 \end{array}\right] = \left[\begin{array}{c} 6\\6 \end{array}\right], \amp \hspace{2cm} \amp \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right]\, \left[\begin{array}{c} -1\\2 \end{array}\right] = \left[\begin{array}{c} 2\\2 \end{array}\right], \amp\hspace{1cm} \amp \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right]\, \left[\begin{array}{c} 1\\1 \end{array}\right] = \left[\begin{array}{c} 4\\4 \end{array}\right]. \end{array} \end{equation*}

Graphically, we can see that the effect of applying the matrix to the vectors is to stretch it and rotate it. Except \(\bA{b}_3\) which it is only stretched, but conserves its direction. This is because \(\bA{b}_3\) is an eigenvector of \(\bA{A}.\)
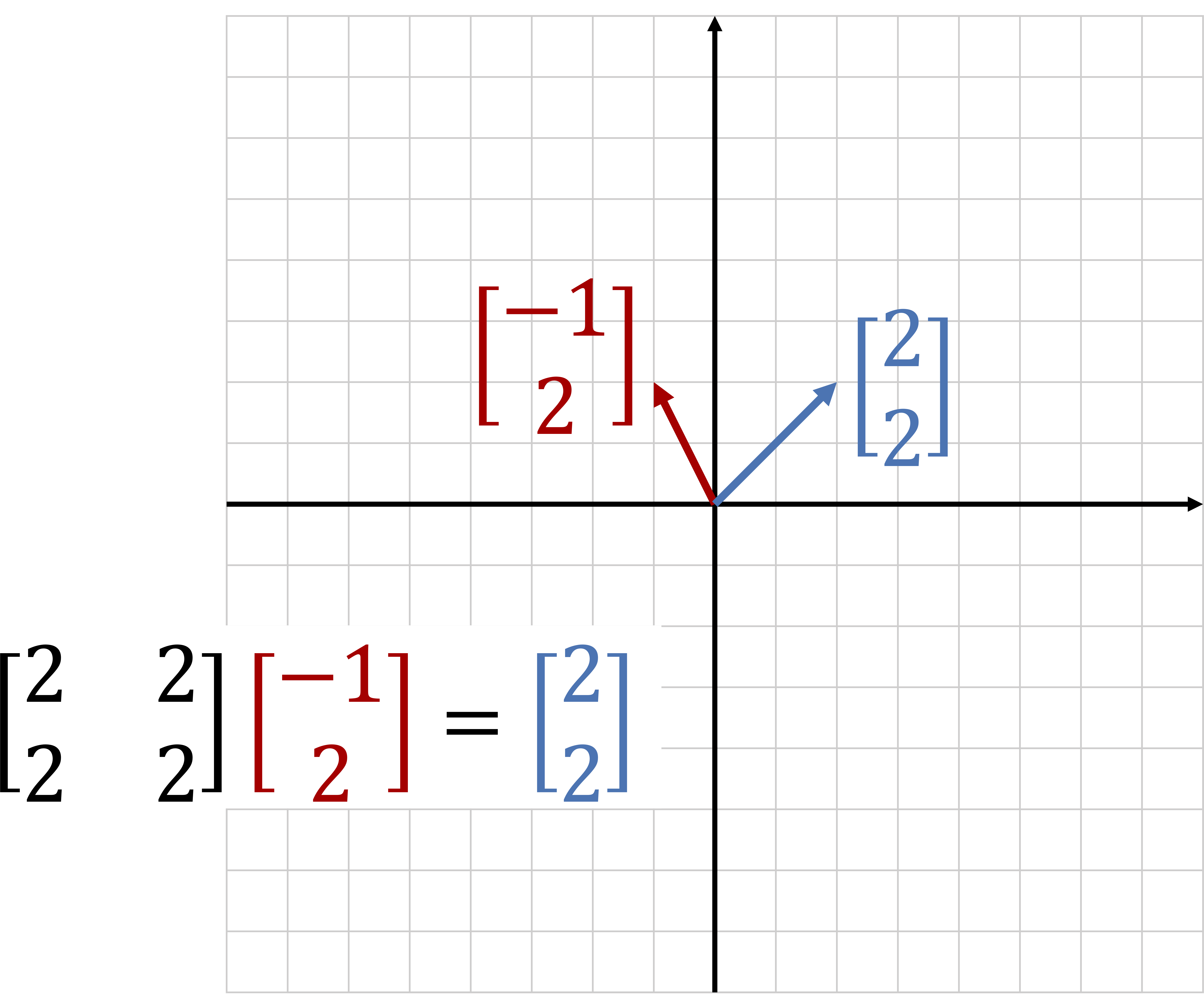
Definition 1.1.1. Eigenvector.

If the product \(\bA{A} \bA{u}\) points in the same direction as the vector \(\bA{u}\text{,}\) we say that \(\bA{u}\) is an eigenvector of \(\bA{A}\text{.}\)

Definition 1.1.2. Eigenvalue.

If \(\bA{u}\) is an eigenvector of \(\bA{A}\) then the following is true.

\begin{equation*} \bA{A} \bA{u} = \lambda \bA{u}, \end{equation*}

where \(\lambda\) is a real or complex number. We call \(\lambda\) the eigenvalue of \(\bA{A}\) associated with the eigenvector \(\bA{u}\text{.}\)

Subsubsection 1.1.1.2 Singular matrices and homogeneous systems

If \(\bA{A}\) is singular matrix, i.e., \(\detA{\bA{A}} = 0,\) we know that this means the system does not have a unique solution. However the system might still have multiple solution.

Consider the system of equations,

\begin{equation*} \begin{array}{rrrrrrr} x_1 \amp-\amp 4x_2 \amp+\amp x_3 \amp=\amp -3\\ x_1 \amp+\amp x_2 \amp-\amp 3x_3 \amp=\amp 6\\ 2x_1\amp- \amp 3x_2 \amp-\amp 2x_3 \amp=\amp 3 \end{array} \end{equation*}

In this case \(\detA{\bA{A}} = 0,\) which implies we cannot use Cramer's or matrix inverse to find its solution. However, we can still reduce the matrix using Gauss-Jordan:

\begin{equation*} \begin{array}{ccc} \left[ \begin{array}{ccc|c} 1 \amp -4 \amp 1 \amp -3\\ 1 \amp 1 \amp -3 \amp 6\\ 2 \amp -3 \amp -2 \amp 3 \end{array}\right] \amp \begin{array}{c}R_2 \rightarrow R_2 - R_1\\ R_3 \rightarrow R_3 - 2R_1\end{array} \amp \left[ \begin{array}{ccc|c} 1 \amp -4 \amp 1 \amp -3\\ 0 \amp 5 \amp -4 \amp 9\\ 0 \amp 5 \amp -4 \amp 9 \end{array}\right] \\ \amp\amp\\ \amp R_3 \rightarrow R_3 - R_2 \amp \left[ \begin{array}{ccc|c} 1 \amp -4 \amp 1 \amp -3\\ 0 \amp 5 \amp -4 \amp 9\\ 0 \amp 0 \amp 0 \amp 0 \end{array}\right] \\ \amp\amp\\ \amp R_2 \rightarrow R_2/5 \amp \left[ \begin{array}{ccc|c} 1 \amp -4 \amp 1 \amp -3\\ 0 \amp 1 \amp -\frac{4}{5} \amp \frac{9}{5}\\ 0 \amp 0 \amp 0 \amp 0 \end{array}\right] \\ \amp\amp\\ \amp R_1 \rightarrow R_1 + 4R_2 \amp \left[ \begin{array}{ccc|c} 1 \amp 0 \amp -\frac{11}{5} \amp -\frac{21}{5}\\ 0 \amp 1 \amp -\frac{4}{5} \amp \frac{9}{5}\\ 0 \amp 0 \amp 0 \amp 0 \end{array}\right] \end{array} \end{equation*}

This means the system has infinitely many solutions:

\begin{equation*} \begin{array}{ccc} x_1 \amp =\amp -\frac{21}{5} + \frac{11}{5} t\\ x_2 \amp =\amp \frac{9}{5} + \frac{4}{5} t\\ x_3 \amp =\amp t, \end{array} \end{equation*}

where \(t\) is any real number.

Insight 1.1.4. Homogeneous systems.

Consider a homogeneous system of linear equations,

\begin{equation*} \bA{A} \bA{x} = \bA{0}. \end{equation*}

If \(\detA{\bA{A}} \ne 0\) then we know that the system has unique solution. However, \(\bA{x} = \bA{0}\) is always a solution to a homogeneous system. This implies that having \(\detA{\bA{A}} \ne 0\) for a homogeneous system means that the only solution is \(\bA{x} = \bA{0}\text{.}\)

Alternatively, if \(\detA{\bA{A}} = 0\) then the system might have infinitely many solutions, meaning a \(\bA{x} \ne \bA{0}\) is also a solution.

Subsection 1.1.2 Finding eigenvalues and eigenvectors

Coming back to the eigenvalue equation,

\begin{equation*} \bA{A} \bA{u} = \lambda \bA{u}, \end{equation*}

we can rearrange it as,

\begin{equation*} \begin{array}{ccc} \bA{A} \bA{u} - \lambda \bA{u} \amp =\amp 0,\\ \left( \bA{A} - \lambda \bA{I} \right) \bA{u} \amp =\amp 0. \end{array} \end{equation*}
  • If \(\detA{ \bA{A} - \lambda \bA{I}} \ne 0\text{,}\) then the only solution will be \(\bA{u} = \bA{0}.\)
  • On the other hand, if \(\detA{\bA{A} - \lambda \bA{I}} = 0,\) there exists a vector \(\bA{u} \ne \bA{0}\) which satisfies the equation. This vector is an eigenvector of \(\bA{A}\) with associated eigenvalue \(\lambda. \)

Subsubsection 1.1.2.1 Characteristic polynomial

Assume that \(\bA{A}\) is an \(n\times n\) matrix. The characteristic polynomial of \(\bA{A}\) is defined as the function \(f(\lambda)\) given by:

\begin{equation*} f(\lambda) = \detA{ \bA{A} - \lambda \bA{I}_n}, \end{equation*}

where \(\bA{I}\) is the Identity matrix.

Find the characteristic polynomial of \(\displaystyle \bA{A} = \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right].\)

We first find the matrix \(\bA{A} - \lambda \bA{I}_2\text{,}\)

\begin{equation*} \begin{array}{ccc} \bA{A} - \lambda \bA{I}_2 \amp=\amp \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right] - \lambda \left[\begin{array}{cc} 1 \amp 0\\ 0\amp 1 \end{array}\right] \\ \amp\amp\\ \amp=\amp \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right] - \left[\begin{array}{cc} \lambda\amp 0\\ 0\amp \lambda \end{array}\right] \\ \amp\amp\\ \amp=\amp \left[\begin{array}{cc} 2 - \lambda \amp 2\\ 2\amp 2 - \lambda \end{array}\right] \end{array} \end{equation*}

Next we find its determinant,

\begin{equation*} \begin{array}{ccc} \detA{ \bA{A} - \lambda \bA{I}_2} = \left|\begin{array}{cc} 2 - \lambda \amp 2\\ 2\amp 2 - \lambda \end{array}\right| \amp=\amp (2 - \lambda ) \cdot \left( 2 - \lambda \right) - 2 \cdot 2 \\ \amp\amp\\ \amp=\amp 4 - 4 \lambda + \lambda^2 - 4\\ \amp\amp\\ \amp=\amp \lambda^2 - 4\lambda \end{array} \end{equation*}

The characteristic polynomial of \(\bA{A}\) is

\begin{equation*} f(\lambda) =\lambda^2 - 4\lambda. \end{equation*}

Subsubsection 1.1.2.2 Finding eigenvalues

The eigenvalues of a matrix are the roots of the characteristic polynomial.

Find the eigenvalues of \(\displaystyle \bA{A} = \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right].\)

From example Example 1.1.6 we have the characteristic polynomial of \(\bA{A}\text{,}\)

\begin{equation*} f(\lambda) =\lambda^2 - 4\lambda. \end{equation*}

To find the roots we solve the equation,

\begin{equation*} \begin{array}{ccc} \lambda^2 - 4\lambda \amp=\amp 0\\ \lambda \left(\lambda - 4 \right) \amp=\amp 0. \end{array} \end{equation*}

The roots, and hence eigenvalues, are

\begin{equation*} \begin{array}{ccc} \lambda_1 \amp=\amp 0,\\ \lambda_2 \amp=\amp 4. \end{array} \end{equation*}

Subsubsection 1.1.2.3 Finding eigenvectors

Given an eigenvalue \(\lambda_i\text{,}\) the corresponding eigenvector \(\bA{u}_i \) is found by solving the following system of equations,

\begin{equation*} \left( \bA{A} - \lambda_i \bA{I} \right) \bA{u}_i = 0.\\ \end{equation*}

Find the eigenvectors of \(\displaystyle \bA{A} = \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right].\)

From example Example 1.1.7, the eigenvalues of \(\bA{A}\) are \(\lambda_1 =0\) and \(\lambda_2 = 4\text{.}\)

  • To find the eigenvector associated to \(\lambda_1\) we solve the following system,

    \begin{equation*} \begin{array}{ccc} \left( \bA{A} - 0 \bA{I}_2 \right) \bA{u} \amp=\amp 0\\ \amp\amp\\ \left[\begin{array}{cc} 2 \amp 2\\ 2\amp 2 \end{array}\right] \left[\begin{array}{c} u_1\\ u_2 \end{array}\right] \amp=\amp \left[\begin{array}{c} 0\\ 0 \end{array}\right] \\ \amp\amp\\ 2u_1 + 2u_2 \amp=\amp 0\\ 2u_1 + 2u_2 \amp=\amp 0 \end{array} \end{equation*}

    A solution to this system is

    \begin{equation*} \bA{u} = \left[\begin{array}{c} 1 \\ -1 \end{array}\right]. \end{equation*}

  • To find the eigenvector associated to \(\lambda_2\) we solve the following system,

    \begin{equation*} \begin{array}{ccc} \left( \bA{A} - 4 \bA{I}_2 \right) \bA{v} \amp=\amp 0\\ \amp\amp\\ \left[\begin{array}{cc} 2 - 4 \amp 2\\ 2\amp 2- 4 \end{array}\right] \left[\begin{array}{c} v_1\\ v_2 \end{array}\right] \amp=\amp \left[\begin{array}{c} 0\\ 0 \end{array}\right] \\ \amp\amp\\ \left[\begin{array}{cc} -2 \amp 2\\ 2\amp -2 \end{array}\right] \left[\begin{array}{c} v_1\\ v_2 \end{array}\right] \amp=\amp \left[\begin{array}{c} 0\\ 0 \end{array}\right] \\ \amp\amp\\ -2v_1 + 2v_2 \amp=\amp 0\\ 2v_1 - 2v_2 \amp=\amp 0 \end{array} \end{equation*}

    A solution to this system is

    \begin{equation*} \bA{u} = \left[\begin{array}{c} 1 \\ 1 \end{array}\right]. \end{equation*}

Subsubsection 1.1.2.4 Examples \(2\times 2\) matrices

Suppose

\begin{equation*} \displaystyle \bA{A} = \left[\begin{array}{ccc} a \amp b\\ c\amp d \end{array}\right]\text{.} \end{equation*}

The characteristic polynomial is

\begin{equation*} \left|\begin{array}{ccc} a-\lambda \amp b\\ c\amp d -\lambda \end{array}\right| = (a-\lambda)(d-\lambda) - b\, c = \lambda^2 - (a+d)\lambda + (a\,d - b\,c). \end{equation*}

This equation can be rewritten as,

\begin{equation*} \lambda^2 - \trA{\bA{A}}\lambda + \detA{\bA{A}}. \end{equation*}

We can solve this equation using the quadratic formula as,

\begin{equation*} \lambda_{1,2} = \frac{\trA{\bA{A}} \pm \sqrt{(\trA{\bA{A}})^2 - 4\detA{\bA{A}}}}{2}. \end{equation*}

Find the eigenvalues and eigenvectors of \(\displaystyle \bA{A} = \left[\begin{array}{cc} 5 \amp -1\\ -4\amp 2 \end{array}\right].\)

  • Find \(\bA{A} - \lambda \bA{I}_2\)
    \begin{equation*} \bA{A}- \lambda \bA{I}_2 = \left[\begin{array}{cc} 5- \lambda \amp -1\\ -4\amp 2- \lambda \end{array}\right]. \end{equation*}
  • Find characteristic polynomial
    \begin{equation*} f(\lambda) = (5-\lambda)(2-\lambda) - 4 = \lambda^2 - 7 \lambda + 6 \end{equation*}
  • Find the roots of the characteristic polynomial
    \begin{equation*} \begin{array}{ccc} \lambda^2 - 7 \lambda + 6 \amp=\amp 0\\ (\lambda-6) (\lambda-1) \amp=\amp 0 \end{array} \end{equation*}
    \begin{equation*} \begin{array}{ccc} \lambda_1 = 1, \hspace{2cm} \lambda_2 = 6. \end{array} \end{equation*}
  • Find eigenvector for \(\lambda_1\text{,}\)
    \begin{equation*} \left(\bA{A}- \bA{I}_2\right) \bA{u}= \left[\begin{array}{cc} 5- 1 \amp -1\\ -4\amp 2- 1 \end{array}\right] \left[\begin{array}{c} u_1\\u_2 \end{array}\right] = \left[\begin{array}{cc} 4 \amp -1\\ -4\amp 1 \end{array}\right] \left[\begin{array}{c} u_1\\u_2 \end{array}\right] = \left[\begin{array}{c} 4u_1 - u_2\\ -4u_1 + u_2 \end{array}\right] \end{equation*}
    \begin{equation*} \left(\bA{A}- \bA{I}_2\right) \bA{u} = \bA{0 } \hspace{1cm} \Rightarrow \hspace{1cm} \left[\begin{array}{c} 4u_1 - u_2\\ -4u_1 + u_2 \end{array}\right] = \left[\begin{array}{c} 0\\0 \end{array}\right] \end{equation*}
    The solution implies \(u_2 = 4 u_1\text{,}\) so that an eigenvector for \(\lambda_1 \) is
    \begin{equation*} \bA{u} = \left[ \begin{array}{c} 1\\4 \end{array}\right]. \end{equation*}
  • Find eigenvector for \(\lambda_2\text{,}\)
    \begin{equation*} \left(\bA{A}- 6 \bA{I}_2\right) \bA{v}= \left[\begin{array}{cc} 5- 6 \amp -1\\ -4\amp 2- 6 \end{array}\right] \left[\begin{array}{c} v_1\\v_2 \end{array}\right] = \left[\begin{array}{cc} -1 \amp -1\\ -4\amp -4 \end{array}\right] \left[\begin{array}{c} v_1\\v_2 \end{array}\right] = \left[\begin{array}{c} -v_1 - v_2\\ -4v_1 - 4v_2 \end{array}\right] \end{equation*}
    \begin{equation*} \left(\bA{A}- 6 \bA{I}_2\right) \bA{v} = \bA{0 } \hspace{1cm} \Rightarrow \hspace{1cm} \left[\begin{array}{c} -v_1 - v_2\\ -4v_1 - 4v_2 \end{array}\right] = \left[\begin{array}{c} 0\\0 \end{array}\right] \end{equation*}
    The solution implies \(v_2 = - v_1\text{,}\) so that an eigenvector for \(\lambda_2 \) is
    \begin{equation*} \bA{v} = \left[ \begin{array}{c} 1\\ -1 \end{array}\right]. \end{equation*}

Find the eigenvalues and eigenvectors of \(\displaystyle \bA{A} = \left[\begin{array}{cc} -2 \amp 4\\ -4\amp 2 \end{array}\right].\)

  • Find \(\bA{A} - \lambda \bA{I}_2\)
    \begin{equation*} \bA{A}- \lambda \bA{I}_2 = \left[\begin{array}{cc} -2 -\lambda \amp 4\\ -4\amp 2- \lambda \end{array}\right]. \end{equation*}
  • Find characteristic polynomial
    \begin{equation*} f(\lambda) = (-2-\lambda)(2-\lambda) +16 = \lambda^2 + 12 \end{equation*}
  • Find the roots of the characteristic polynomial
    \begin{equation*} \begin{array}{ccc} \lambda^2 + 12 \amp=\amp 0\\ \lambda^2 \amp=\amp -12 \end{array} \end{equation*}
    \begin{equation*} \lambda_1 = 2\sqrt{3} i, \hspace{2cm} \lambda_2 = -2\sqrt{3}i. \end{equation*}
  • Find eigenvector for \(\lambda_1\text{,}\)
    \begin{equation*} \left(\bA{A}- 2\sqrt{3} i \bA{I}_2\right) \bA{u}= \left[\begin{array}{cc} -2 -2\sqrt{3} i \amp 4\\ -4\amp 2- 2\sqrt{3} i \end{array}\right] \left[\begin{array}{c} u_1\\u_2 \end{array}\right] = \left[\begin{array}{c} -2u_1 - 2\sqrt{3}i\, u_1 + 4u_2\\ -4u_1 + 2u_2 - 2\sqrt{3}i\,u_2 \end{array}\right] \end{equation*}
    Using the first equation we get,
    \begin{equation*} -2u_1 - 2\sqrt{3}i\, u_1 + 4u_2 = 0 \hspace{1cm} \Rightarrow \hspace{1cm} u_2 = \frac{1}{2} u_1 + \frac{\sqrt{3} i}{2} u_1 = \left(\frac{1}{2} + \frac{\sqrt{3} i}{2}\right) u_1 \end{equation*}
    An eigenvector is then,
    \begin{equation*} \bA{u} = \left[ \begin{array}{c} 2\\ 1 + \sqrt{3} i\ \end{array}\right]. \end{equation*}
  • Find eigenvector for \(\lambda_2\text{,}\)
    \begin{equation*} \left(\bA{A} + 2\sqrt{3} i \bA{I}_2\right) \bA{v}= \left[\begin{array}{cc} -2 +2\sqrt{3} i \amp 4\\ -4\amp 2+ 2\sqrt{3} i \end{array}\right] \left[\begin{array}{c} v_1\\v_2 \end{array}\right] = \left[\begin{array}{c} -2v_1 + 2\sqrt{3}i\, v_1 + 4v_2\\ -4v_1 + 2v_2 + 2\sqrt{3}i\,v_2 \end{array}\right] \end{equation*}
    Using the first equation we get,
    \begin{equation*} -2v_1 + 2\sqrt{3}i\, v_1 + 4v_2 \hspace{1cm} \Rightarrow \hspace{1cm} v_2 = \left(\frac{1}{2} - \frac{\sqrt{3} i}{2}\right) v_1 \end{equation*}
    An eigenvector is then,
    \begin{equation*} \bA{v} = \left[ \begin{array}{c} 2\\ 1 -\sqrt{3} i\ \end{array}\right]. \end{equation*}

Find the eigenvalues and eigenvectors of \(\displaystyle \bA{A} = \left[\begin{array}{cc} 7 \amp 1\\ -4\amp 3 \end{array}\right].\)

  • Find \(\bA{A} - \lambda \bA{I}_2\)
    \begin{equation*} \bA{A}- \lambda \bA{I}_2 = \left[\begin{array}{cc} 7-\lambda \amp 1\\ -4\amp 3-\lambda \end{array}\right]. \end{equation*}
  • Find characteristic polynomial
    \begin{equation*} f(\lambda) = (7-\lambda )(3-\lambda) +4 = \lambda^2 - 10 \lambda + 25 = \left(\lambda - 5\right)^2 \end{equation*}
  • Find the roots of the characteristic polynomial
    \begin{equation*} \begin{array}{ccc} \left(\lambda - 5\right)^2 \amp=\amp 0 \end{array} \end{equation*}
    \begin{equation*} \lambda_{1,2} = 5 \end{equation*}
    Insight 1.1.12.
    A repeated eigenvalue is called a defective eigenvalue.
  • Find eigenvector for \(\lambda_1\text{,}\)
    \begin{equation*} \left(\bA{A}- 5 \bA{I}_2\right) \bA{u}= \left[\begin{array}{cc} 7-5 \amp 1\\ -4\amp 3-5 \end{array}\right] \left[\begin{array}{c} u_1\\u_2 \end{array}\right] = \left[\begin{array}{cc} 2 \amp 1\\ -4\amp -2 \end{array}\right] \left[\begin{array}{c} u_1\\u_2 \end{array}\right]= \left[\begin{array}{c} -2u_1 - u_2\\ -4u_1 - 2u_2 \end{array}\right] \end{equation*}
    \begin{equation*} \left(\bA{A}- 5\bA{I}_2\right) \bA{u} = \bA{0 } \hspace{1cm} \Rightarrow \hspace{1cm} \left[\begin{array}{c} -2u_1 - u_2\\ -4u_1 - 2u_2 \end{array}\right] = \left[\begin{array}{c} 0\\0 \end{array}\right] \end{equation*}
    Using the first equation we get, \(u_2 = -2 u_1\text{,}\) so that an eigenvector is
    \begin{equation*} \bA{u} = \left[ \begin{array}{c} 1\\-2 \end{array}\right]. \end{equation*}
    We can only obtain one eigenvector associated to the repeated eigenvalue, this means that only \(\bA{u}\) or multiples of it can satisfy,
    \begin{equation*} \bA{A} \bA{u} = 5 \bA{u} \hspace{1cm} \Rightarrow \hspace{1cm} (\bA{A} - 5 \bA{I}) \bA{u} = \bA{0}. \end{equation*}
    The next best thing we can get is a vector that satisfies the following relation,
    \begin{equation*} (\bA{A} - 5 \bA{I}) \bA{v} = \bA{u}. \end{equation*}
    We call the vector \(\bA{v}\) a generalized eigenvector.
  • Find the generalized eigenvector for \(\lambda = 5\)
    \begin{equation*} \begin{array}{ccc} (\bA{A} - 5 \bA{I}) \bA{v} \amp=\amp \bA{u}\\ \amp\amp\\ \left[\begin{array}{cc} 2 \amp 1\\ -4\amp -2 \end{array}\right] \left[\begin{array}{c} v_1\\v_2 \end{array}\right] \amp=\amp \left[ \begin{array}{c} 1\\-2 \end{array}\right]\\ \amp\amp\\ \left[\begin{array}{c} 2v_1 + v_2\\ -4v_1 -2v_2 \end{array}\right] \amp=\amp \left[ \begin{array}{c} 1\\-2 \end{array}\right] \end{array} \end{equation*}
    Using the first equation we get,
    \begin{equation*} 2v_1 + v_2 = 1 \hspace{1cm} \Rightarrow \hspace{1cm} v_2 = 1 - 2v_1. \end{equation*}
    A generalized eigenvectors is then,
    \begin{equation*} \bA{v} = \left[ \begin{array}{c} 0\\ 1 \end{array}\right]. \end{equation*}

Subsubsection 1.1.2.5 Example \(3\times 3\) matrices

Find the eigenvalues and eigenvectors of \(\displaystyle \bA{A} = \left[\begin{array}{ccc} 13\amp0 \amp-15\\ -3\amp 4 \amp 9\\ 5 \amp0\amp-7 \end{array}\right]\)

  • Find \(\bA{A} - \lambda \bA{I}_3\)
    \begin{equation*} \bA{A} - \lambda \bA{I}_3 = \left[\begin{array}{ccc} 13\amp0 \amp-15\\ -3\amp 4 \amp 9\\ 5 \amp0\amp-7 \end{array}\right] - \left[\begin{array}{ccc} \lambda \amp 0 \amp 0\\ 0 \amp \lambda \amp 0\\ 0\amp 0 \amp \lambda \end{array}\right] = \left[\begin{array}{ccc} 13-\lambda\amp0 \amp-15\\ -3\amp 4-\lambda \amp 9\\ 5 \amp0\amp-7-\lambda \end{array}\right] \end{equation*}
  • Find characteristic polynomial
    \begin{equation*} \begin{array}{ccc} f(\lambda) = \left|\begin{array}{ccc} 13-\lambda\amp0 \amp-15\\ -3\amp 4-\lambda \amp 9\\ 5 \amp0\amp-7-\lambda \end{array}\right| \amp=\amp (4-\lambda) \left|\begin{array}{cc} 13-\lambda \amp-15\\ 5 \amp-7-\lambda \end{array}\right|\\ \amp=\amp (4-\lambda) \left( (13-\lambda)(-7-\lambda) + 75\right)\\ \amp=\amp (4-\lambda) \left( \lambda^2 - 6\lambda -16 \right)\\ \amp=\amp (4-\lambda) ( \lambda- 8) (\lambda +2 )\\ \end{array} \end{equation*}
  • Find the roots of the characteristic polynomial
    \begin{equation*} (4-\lambda) ( \lambda- 8) (\lambda +2 ) = 0 \end{equation*}
    \begin{equation*} \lambda_1 = 8, \hspace{0.5cm} \lambda_2 = 4, \hspace{0.5cm} \lambda_3 = -2 \end{equation*}
  • Find eigenvector for \(\lambda_1 = 8\text{,}\)
    \begin{equation*} \begin{array}{ccc} ( \bA{A} - 8 \bA{I}_3) \bA{u} = \left[\begin{array}{ccc} 13-8\amp0 \amp-15\\ -3\amp 4-8 \amp 9\\ 5 \amp0\amp-7-8 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right] \amp=\amp \left[\begin{array}{ccc} 5\amp0 \amp-15\\ -3\amp -4 \amp 9\\ 5 \amp0\amp-15 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right]\\ \amp\amp\\ \amp=\amp\left[ \begin{array}{c} 5u_1 - 15u_3\\ -3u_1 -4u_2 + 9u_3\\ 5u_1 - 15u_3 \end{array}\right] \end{array} \end{equation*}
    From the first equation we have,
    \begin{equation*} 5u_1 - 15u_3 = 0 \hspace{1cm} \Rightarrow u_1 = 3u_3 \end{equation*}
    Combining this with the second equation gives,
    \begin{equation*} \begin{array}{ccc} -3u_1 -4u_2 + 9u_3 \amp=\amp 0\\ -9u_3 - 4u_2 + 9u_3 \amp=\amp0\\ -4u_2 \amp=\amp 0. \end{array} \end{equation*}
    Then, an eigenvector for \(\bA{A}\) associated with \(\lambda_1 =8\) is
    \begin{equation*} \left[ \begin{array}{c} 3\\0\\1 \end{array}\right]. \end{equation*}

  • Find eigenvector for \(\lambda_2 = 4\text{,}\)

    \begin{equation*} \begin{array}{ccc} (\bA{A} - 4 \bA{I}_3) \bA{u} = \left[\begin{array}{ccc} 13-4\amp0 \amp-15\\ -3\amp 4-4 \amp 9\\ 5 \amp0\amp-7-4 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right] \amp=\amp \left[\begin{array}{ccc} 9\amp0 \amp-15\\ -3\amp 0 \amp 9\\ 5 \amp0\amp-11 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right]\\ \amp\amp\\ \amp=\amp\left[ \begin{array}{c} 9u_1 - 15u_3\\ -3u_1 + 9u_3\\ 5u_1 - 11u_3 \end{array}\right]. \end{array} \end{equation*}

    The only way in which the three equations can be satisfied simultaneously is if \(u_1 = u_3 = 0\text{.}\)

    Then, an eigenvector for \(\bA{A}\) associated with \(\lambda_2 =4\) is

    \begin{equation*} \left[ \begin{array}{c} 0\\1\\0 \end{array}\right]. \end{equation*}
  • Find eigenvector for \(\lambda_3 = -2\text{,}\)
    \begin{equation*} \begin{array}{ccc} (\bA{A} +2 \bA{I}_3) \bA{u} = \left[\begin{array}{ccc} 13+2\amp0 \amp-15\\ -3\amp 4+2 \amp 9\\ 5 \amp0\amp-7+2 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right] \amp=\amp \left[\begin{array}{ccc} 15\amp0 \amp-15\\ -3\amp 6 \amp 9\\ 5 \amp0\amp-5 \end{array}\right] \left[ \begin{array}{c} u_1\\u_2\\u_3 \end{array}\right]\\ \amp\amp\\ \amp=\amp\left[ \begin{array}{c} 15u_1 - 15u_3\\ -3u_1 +6u_2 + 9u_3\\ 5u_1 - 5u_3 \end{array}\right] \end{array} \end{equation*}
    From the first equation we have,
    \begin{equation*} 15u_1 - 15u_3 = 0 \hspace{1cm} \Rightarrow u_1 = u_3 \end{equation*}
    Combining this with the second equation gives,
    \begin{equation*} \begin{array}{ccc} -3u_1 +6u_2 + 9u_3\\ -3u_3 +6u_2 + 9u_3 \amp=\amp0\\ 6u_3 + 6u_2 \amp=\amp 0 \hspace{1cm} \Rightarrow u_2 = - u_3. \end{array} \end{equation*}
    Then, an eigenvector for \(\bA{A}\) associated with \(\lambda_3 =-2\) is
    \begin{equation*} \left[ \begin{array}{c} 1\\-1\\1 \end{array}\right]. \end{equation*}

Subsection 1.1.3 Properties of eigenvalues and eigenvectors

Subsubsection 1.1.3.1 Determinant and eigenvalues product

The product of the eigenvectors of a matrix is equal to the determinant of the matrix

\begin{equation*} \detA{\bA{A}} = \lambda_n \cdot \lambda_{n-1} \cdots \lambda_2 \cdot \lambda_1. \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} 5 \amp-1\\ -4 \amp2 \end{array}\right]\) in Example 1.1.9 with eigenvectors \(\lambda_1 = 1\) and \(\lambda_2 = 6\) we have,

\begin{equation*} \detA{\bA{A}} = 5 \cdot 2 - (-1) \cdot (-4) = 10 - 4 = \mathbf{ ~ 6} \boldsymbol{~ = ~} \lambda_1 \cdot \lambda_2 = 1 \cdot 6 \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} -2 \amp 4\\ -4 \amp 2 \end{array}\right]\) in Example 1.1.10 with eigenvectors \(\lambda_1 = 2\sqrt{3}\,i\) and \(\lambda_2 = -2\sqrt{3}\,i\) we have,

\begin{equation*} \detA{\bA{A}} = (-2) \cdot 2 - (4) \cdot (-4) = -4 + 16 = \mathbf{ ~ 12} \boldsymbol{~ = ~} \lambda_1 \cdot \lambda_2 = 2\sqrt{3}\,i \cdot (-2\sqrt{3}\,i) = 4 \cdot 3 \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} 7\amp1 \\ -4 \amp 3 \end{array}\right]\) in Example 1.1.11 with eigenvectors \(\lambda_1 = 5\) and \(\lambda_2 = 5\) we have,

\begin{equation*} \detA{\bA{A}} = 7 \cdot 3 - (1) \cdot (-4) = 21 + 4 = \mathbf{ ~ 25} \boldsymbol{~ = ~} \lambda_1 \cdot \lambda_2 = 5 \cdot 5 \end{equation*}

Subsubsection 1.1.3.2 Trace and eigenvalues sum

The sum of the eigenvectors of a matrix is equal to the trace of the matrix

\begin{equation*} \trA{\bA{A}} = \lambda_n + \lambda_{n-1} + \cdots + \lambda_2 + \lambda_1. \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} 5 \amp-1\\ -4 \amp2 \end{array}\right]\) in Example 1.1.9 with eigenvectors \(\lambda_1 = 1\) and \(\lambda_2 = 6\) we have,

\begin{equation*} \trA{\bA{A}} = 5 + 2 = \mathbf{ ~ 7} \boldsymbol{~ = ~} \lambda_1 + \lambda_2 = 1 + 6 \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} -2 \amp 4\\ -4 \amp 2 \end{array}\right]\) in Example 1.1.10 with eigenvectors \(\lambda_1 = 2\sqrt{3}\,i\) and \(\lambda_2 = -2\sqrt{3}\,i\) we have,

\begin{equation*} \trA{\bA{A}} = (-2) + 2 = \mathbf{ ~ 0} \boldsymbol{~ = ~} \lambda_1 + \lambda_2 = 2\sqrt{3}\,i -2\sqrt{3}\,i \end{equation*}

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} 7\amp1 \\ -4 \amp 3 \end{array}\right]\) in Example 1.1.11 with eigenvectors \(\lambda_1 = 5\) and \(\lambda_2 = 5\) we have,

\begin{equation*} \trA{\bA{A}} = 7 + 3 = \mathbf{ ~ 10} \boldsymbol{~ = ~} \lambda_1 + \lambda_2 = 5 + 5 \end{equation*}

Subsubsection 1.1.3.3 Eigenvalues and matrix singularity

If \(\bA{A}\) is a singular matrix, then \(\lambda = 0\) is an eigenvalue of \(\bA{A}\text{.}\)

\begin{equation*} \bA{A} = \left[\begin{array}{cc} 2 \amp 2\\ 1 \amp 1 \end{array}\right] \end{equation*}
\begin{equation*} \detA{\bA{A}} = 2 - 2 =0. \end{equation*}
\begin{equation*} \detA{\bA{A}-\lambda \bA{I}_2} = \left|\begin{array}{cc} 2-\lambda \amp 2\\ 1 \amp 1-\lambda \end{array}\right| = (2-\lambda)(1-\lambda) - 2 = \lambda^2 -3 \lambda \end{equation*}

The eigenvalues of \(\bA{A}\) are \(\lambda_1 = 0\) and \(\lambda_2 = 3\text{.}\)

Subsubsection 1.1.3.4 Eigenvalues and eigenvectors of matrix powers

  • The eigenvectors of \(\bA{A}^p\text{,}\) for any integer \(p\text{,}\) are the same as the eigenvectors of \(\bA{A}\text{.}\)
  • If \(\lambda_i\) is an eigenvalue of \(\bA{A}\) then \(\lambda_i^p\) is an eigenvalue of \(\bA{A}^p\text{.}\)

For \(\displaystyle \bA{A} = \left[\begin{array}{cc} 5 \amp-1\\ -4 \amp2 \end{array}\right]\) in Example 1.1.9 with eigenvalue \(\lambda_1 = 1\) and eigenvector \(\displaystyle \bA{u} = \left[\begin{array}{c} 1\\4\end{array}\right]\text{,}\) we have,

\begin{equation*} \begin{array} \bA{A} \bA{u} = \bA{u} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 5 \amp-1\\ -4 \amp2 \end{array}\right] \left[\begin{array}{c} 1\\4\end{array}\right] = \left[\begin{array}{c} 1\\4\end{array}\right]\\ \amp\amp\\ \bA{A}^2 \bA{u} = \bA{A} \left(\bA{A} \bA{u}\right) = \bA{A} \bA{u} = \bA{u} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 29\amp -7\\ -28 \amp 8 \end{array}\right] \left[\begin{array}{c} 1\\4\end{array}\right] = \left[\begin{array}{c} 1\\4\end{array}\right]\\ \amp\amp\\ \bA{A}^3 \bA{u} = \bA{A} \left(\bA{A}^2 \bA{u}\right) =\bA{A} \bA{u} = \bA{u} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 173 \amp -43\\ -172 \amp 44 \end{array}\right] \left[\begin{array}{c} 1\\4\end{array}\right] = \left[\begin{array}{c} 1\\4\end{array}\right] \end{array} \end{equation*}

\(\, \)

For eigenvalue \(\lambda_2 = 6\) and eigenvector \(\displaystyle \bA{u} = \left[\begin{array}{c} 1\\-1\end{array}\right]\text{,}\) we have,

\begin{equation*} \begin{array}{ccc} \bA{A} \bA{v} = 6 \bA{v} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 5 \amp-1\\ -4 \amp2 \end{array}\right] \left[\begin{array}{c} 1\\-1\end{array}\right] = \left[\begin{array}{c} 6\\-6\end{array}\right] = 6 \left[\begin{array}{c} 1\\-1\end{array}\right] \\ \amp\amp\\ \bA{A}^2 \bA{v} = \bA{A} \left(\bA{A} \bA{v}\right) = \bA{A} \left(6 \bA{v}\right) =6 \bA{A} \bA{v} =6^2 \bA{v} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 29\amp -7\\ -28 \amp 8 \end{array}\right] \left[\begin{array}{c} 1\\-1\end{array}\right] = \left[\begin{array}{c} 36\\-36\end{array}\right] = 6^2 \left[\begin{array}{c} 1\\-1\end{array}\right]\\ \amp\amp\\ \bA{A}^3 \bA{v} = \bA{A} \left(\bA{A}^2 \bA{v}\right) = \bA{A} \left(6^2 \bA{v}\right) = 6^2\bA{A} \bA{v} = 6^3\bA{v} \amp\hspace{0.5cm} \Rightarrow \hspace{0.5cm} \amp \left[\begin{array}{cc} 173 \amp -43\\ -172 \amp 44 \end{array}\right] \left[\begin{array}{c} 1\\-1\end{array}\right] = \left[\begin{array}{c} 216\\-216\end{array}\right] = 6^3 \left[\begin{array}{c} 1\\-1\end{array}\right] \end{array} \end{equation*}

Subsubsection 1.1.3.5 Eigenvalues of triangular matrices

If \(\bA{A}\) is a \(n \times n\) triangular matrix, the eigenvalues of \(\bA{A}\) are the diagonal entries of \(\bA{A}\text{.}\)

Find the eigenvalues of \(\displaystyle \bA{A} = \left[\begin{array}{ccc} 1 \amp 2\\ 0 \amp 3 \end{array}\right]\text{.}\)

\begin{equation*} \detA{\bA{A}-\lambda \bA{I}_2} = \left|\begin{array}{ccc} 1-\lambda \amp 2\\ 0 \amp 3-\lambda \end{array}\right| = (1-\lambda)(3-\lambda) \end{equation*}

The eigenvalues of \(\bA{A}\) are \(\lambda_1 = 1\) and \(\lambda_2 = 3\text{.}\)

Find the eigenvalues of \(\displaystyle \bA{A} = \left[\begin{array}{ccc} -2 \amp 0\\ 1 \amp 3 \end{array}\right]\text{.}\)

\begin{equation*} \detA{\bA{A}-\lambda \bA{I}_2} = \left|\begin{array}{ccc} -2-\lambda \amp 0\\ 1 \amp 3-\lambda \end{array}\right| = (-2-\lambda)(3-\lambda) \end{equation*}

The eigenvalues of \(\bA{A}\) are \(\lambda_1 = -2\) and \(\lambda_2 = 3\text{.}\)

Find the eigenvalues of \(\displaystyle \bA{A} = \left[\begin{array}{ccc} 5 \amp 0\\ 0\amp 20 \end{array}\right]\text{.}\)

\begin{equation*} \detA{\bA{A}-\lambda \bA{I}_2} = \left|\begin{array}{ccc} 5-\lambda \amp 0\\ 0 \amp 20-\lambda \end{array}\right| = (5-\lambda)(20-\lambda) \end{equation*}

The eigenvalues of \(\bA{A}\) are \(\lambda_1 = 5\) and \(\lambda_2 = 20\text{.}\)

Subsubsection 1.1.3.6 Eigenvalues of a transpose

Eigenvalues are invariant under transpose

Given \(\displaystyle \bA{A} = \left[\begin{array}{ccc} 5 \amp 4\\ 2\amp 3 \end{array}\right]\text{,}\) find the eigenvalues of \(\bA{A}\) and \(\bA{A}^{\mathsf{T}}\text{.}\)

\begin{equation*} \detA{\bA{A}-\lambda \bA{I}_2} = \left|\begin{array}{ccc} 5-\lambda \amp 4\\ 2 \amp 3-\lambda \end{array}\right| = (5-\lambda)(3-\lambda) - 8 = \lambda^2 - 8\lambda + 7 = (\lambda-7)(\lambda-1) \end{equation*}

The eigenvalues of \(\bA{A}\) are \(\lambda_1 = 7\) and \(\lambda_2 = 1 \)

\begin{equation*} \detA{\bA{A}^{\mathsf{T}}-\lambda \bA{I}_2} = \left|\begin{array}{ccc} 5-\lambda \amp 2\\ 4 \amp 3-\lambda \end{array}\right| = (5-\lambda)(3-\lambda) - 8 = \lambda^2 - 8\lambda + 7 = (\lambda-7)(\lambda-1) \end{equation*}

The eigenvalues of \(\bA{A}^{\mathsf{T}}\) are \(\lambda_1 = 7\) and \(\lambda_2 = 1 \)

Subsubsection 1.1.3.7 Eigenvalues of symmetric matrices

The eigenvalues of a symmetric matrix are real.