Fourier Analysis - Fall 2006
Professor Robert Sharpley
Meets: MWF 12:30-1:45 in
LeConte College 310
Office: LeConte 313 D, and Sumwalt 206.
Office Hours: TuTh 1:45-3:00 and by appointment.
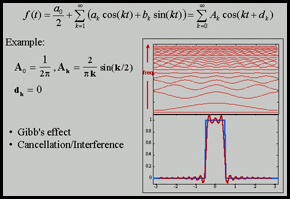
|
MATH 750
Fourier Analysis - Fall 2006 Office: LeConte 313 D, and Sumwalt 206. Office Hours: TuTh 1:45-3:00 and by appointment. |
 |
|
|
|
||
Course Announcements For Sunday, Sept 3, 2006:
|
Course Topics
The course is the study of the basic principles of Fourier analysis.
Lectures will drawn from several references (listed below) and
will include the following topics:
Fourier series of periodic functions and the Fourier transform on the line: representation of functions, i.e. convergence and divergence (point-wise sense, in the norms of various function spaces, and almost everywhere), convergence of Fejer means and summability; Parseval's relation and the square summable theory; conjugate Fourier series, the conjugate function and the Hilbert transform, the Hardy-Littlewood maximal operator, the Riesz-Thorin and Marcinkiewicz interpolation theorems, function spaces, Riesz' theorem. Additional topics may include Poisson summation formula, unconditional convergence of Fourier series; introduction to Fourier multipliers and wavelets.
Applications will include topics in the theory of partial differential equations and signal processing, in particular the FFT.
Prerequisites
Real Analysis
(Math 703-704)
Lectures:
Link to Weekly Outline
Primary Reference
([ISBN-13: 9780521543590 | ISBN-10: 0521543592],
Call #: QA403 .K3).
Additional References
Course Grading
Assigned Homework (50%), Mid-term exam (25%) and Final (25%).
Homework Assignments & Other Course Materials
Check this Link for homework
assignments and other course materials.
|
|
|
![[USC logo]](usclogo.gif)
|
|
| This page maintained by Robert Sharpley
(sharpley@math.sc.edu)
and last updated May 6, 2006. This page ©2006-2007, The Board of Trustees of the University of South Carolina. URL: http://www.math.sc.edu/~sharpley/math750 |
|