ANALYSIS II
Metric Spaces: Compactness
Defn
A collection of
open sets is said to be an open cover
for a set A if the union of the collection contains A. A subset of an open
cover whose union also contains the set A is called a subcover
of the original cover. A cover is
called finite if
it has finitely many members.
Defn
A set K in a metric
space (X,d) is said to be compact
if each open cover of K has
a finite subcover.
Theorem Each
compact set K in a metric space is closed and bounded.
Proposition Each
closed subset of a compact set is also compact.
Theorem (Heine-Borel Theorem
from last term) Each closed and
bounded interval [a,b] is a compact subset of the real numbers.
Pf: Let C
be an open cover for [a,b] and consider the set A := {x
| [a,x] has an open cover from C }.
Note that A is not empty since a belongs to A. Let c:= lub (A). It
is enough to show that c > b , since if x1 belongs
to A and a 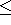 x
x
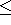 x1
, then x belongs to A. Suppose instead that c
x1
, then x belongs to A. Suppose instead that c 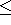 b
, then there must be some O0 in
C such that c belongs to O0 . But
O0 is open, so there exists
b
, then there must be some O0 in
C such that c belongs to O0 . But
O0 is open, so there exists
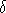 > 0 so that N
> 0 so that N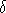 (c)
is contained in O0. Since
c is the least upper bound for A , then there is an x in A such that c-
(c)
is contained in O0. Since
c is the least upper bound for A , then there is an x in A such that c-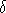 <x
<x
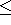 c.
But x belongs to A so there are members O1
, ... , On of C
whose union covers [a,x] . The collection O1
, ... , On covers [a , c+
c.
But x belongs to A so there are members O1
, ... , On of C
whose union covers [a,x] . The collection O1
, ... , On covers [a , c+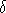 /2]
. Contradiction, since c is the least upper bound for the
set A .
/2]
. Contradiction, since c is the least upper bound for the
set A .
Corollary
Each closed and bounded set of real numbers is compact.
Theorem If
a set A is compact in a metric space X and f: X  Y
is continuous, then f[A] is compact in Y.
Y
is continuous, then f[A] is compact in Y.
Corollary
If f : X  Y
is continuous and X is compact, then f is a bounded function.
Y
is continuous and X is compact, then f is a bounded function.
Corollary
If f : X  R
is continuous and X is compact, then f attains its extremal values.
R
is continuous and X is compact, then f attains its extremal values.
Theorem Suppose
that f: [a,b]® K is one-to-one, onto and
continuous, then f-1 is continuous.
Pf. Let O Í [a,b] be
relatively open, then (f-1)-1(O) = f(O). Let C be
the complement in [a,b] of O, then C is closed and hence compact. Therefore
f(C) is compact in K and conseqently it is closed. Its complement in K
must then be relatively open. That complement however is f(O). [¯]
Compactness Characterization
Theorem Suppose that K is a subset
of a metric space X, then the following are equivalent:
- K is compact.
- each infinite subset of K has a
limit point in K.
- each sequence from K has a subsequence
that converges in K.
(Click
here for the details of the proofs.)
Corollary Each
closed and bounded set K in Rk (or Ck) is compact.
Pf: Use the sequential convergence
criterium and consider projections into each coordinate. Recall that convergence
in Rk is equivalent to convergence in each coordinate.
Defn
A set K in a metric
space X is said to be totally bounded,
if for each  > 0 there
are a finite number of open balls with radius
> 0 there
are a finite number of open balls with radius  which
cover K. Here the centers of the balls and the total number will depend
in general on
which
cover K. Here the centers of the balls and the total number will depend
in general on  .
.
Theorem A
set K in a metric space is compact if and only if it is complete and totally
bounded.
[Homework.]
Robert Sharpley Feb 14 1998
![]() x
x
![]() x1
, then x belongs to A. Suppose instead that c
x1
, then x belongs to A. Suppose instead that c ![]() b
, then there must be some O0 in
C such that c belongs to O0 . But
O0 is open, so there exists
b
, then there must be some O0 in
C such that c belongs to O0 . But
O0 is open, so there exists
![]() > 0 so that N
> 0 so that N![]() (c)
is contained in O0. Since
c is the least upper bound for A , then there is an x in A such that c-
(c)
is contained in O0. Since
c is the least upper bound for A , then there is an x in A such that c-![]() <x
<x
![]() c.
But x belongs to A so there are members O1
, ... , On of C
whose union covers [a,x] . The collection O1
, ... , On covers [a , c+
c.
But x belongs to A so there are members O1
, ... , On of C
whose union covers [a,x] . The collection O1
, ... , On covers [a , c+![]() /2]
. Contradiction, since c is the least upper bound for the
set A .
/2]
. Contradiction, since c is the least upper bound for the
set A .