Compactness Characterization
Theorem
Suppose that K is a subset of a metric space
X, then the following are equivalent:
> 0 there
are a finite number of open balls with radius which
cover K. Here the centers of the balls and the total number will depend
in general on .
Defn A set D is said to be dense in a set A if each neighborhood of each point x of A contains a member from D. A set A in a metric space is called separable if it has a countable dense subset.
(Compactness 
the
Bolzanno-Weierstrass property)
Suppose K is compact, but that A is an infinite
subset of K with no limit point in K. But K is closed since it is compact,
so the derived set of A is empty and A is therefore closed. In particular,
each point of A must be isolated. Hence for each x in A there is a ball
Bx which contains only a single member from A (namely x). The
collection of these balls (together with the complement of A),
{Bx
| x belongs to A}
{Ac}
is an open cover for K. In any finite subcover (which must exist by the compactness of K), one of the balls must contain an infinite number of elements of A since A is infinite. Contradiction, since each one of these balls has exactly one member from A.
(Bolzanno-Weierstrass property
Sequential Compactness)
Suppose {xn}n is
a sequence in K and K has the Bolzanno-Weierstrass property. If the range
of the sequence is finite, we are done since one of the values must be
repeated infinitely often and then that subsequence converges since it
is a constant sequence. In the case the range of the sequence is infinite,
we apply the B-W property to obtain a limit point x0 in K. A
subsequence is then easily constructed which converges to x0
.
(Sequential Compactness Completeness)
[Homework]
(Sequential Compactness Totally
Bounded)
[Homework]
(Hint: Suppose not, then by induction there exists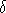 
>
0 and a sequence of points x1,
..., xn,... such that xn+1
does not belong to the B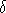(x0)
... B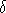(xn)
. This will give rise to a contradiction since all members of the sequence
are at least 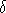units apart and
there can be no convergent subsequence. )
(Sequential Compactness
separable and that the topology has a countable base)
K is totally bounded so there are a finite
number of balls B1(x1,1),
..., B1(x1,n(1)), of radius
1 which cover K. Continuing with each natural number k, we find a finite
number of balls B1/k(xk,1),
..., B1/k(xk,n(k))
which cover K. The collection of all centers then forms a countable dense
subset of K. [Homework:
Prove this] Moreover, for each point
x0 in K and each neighborhood O
of x0 , there is a ball from this countable list containing
x0 which is contained in O,
i.e. the topology of K has a `countable
base'. Notice, in fact, that
each open set can be written as a union of this countable collection of
open balls.
(Sequential Compactness
each open cover of K has a countable subcover)
Let C
be an open cover of K. Each point x in K belongs to some Ox
in C . There is a countable
base (of balls) {Bn}n for the topology so there
exists a natural number n(x) so that x belongs to Bn(x) which
is contained in Ox. For each of these balls Bn
which arise in this way, select one such Ox and (abusing
our notation and thereby our sensibilities) label it On
. This constructs the desired countable subcover of C
.
(Sequential Compactness Compactness)
Let C
be an open cover for a sequentially compact set K. Let {O1
, ..., On , ...} be a countable subcover of C
which covers K. If {O1 , ..., Ok
} is not a finite subcover of K, then there is a member of K, xk+1
say, which lies outside the union of this finite collection. By sequentially
compactness, there is a subsequence {yj} of {xk}
which converges to some y0 in K. Contradiction, since
y0 will be in one of these open sets and by the definition of convergence,
all but a finite number of the yj's will also belong to this same
set. But this is impossible by our construction.
Note If one looks closely, we have in fact shown another important characterization of compactness in metric spaces:
Theorem A set K in a metric space is compact if and only if it is complete and totally bounded.
[Extra Credit Homework]