lab1.mws
lab1.mws
Objectives
The purpose of this Maple worksheet is to provide a first exposure to Maple. Specific goals you should learn as a result of completing this worksheet include:
-
Entering a function (or an expression) in Maple.
-
Using Maple to plot a function.
-
Extracting information from a Maple plot.
What is Maple?
Much of your mathematical background has probably been focused on developing the ability to solve equations and explore functions. The sophisticated manipulation of symbols and expressions that you use to solve equations and investigate functions can also be performed by a
computer algebra system
(CAS). A CAS can be use to generate the
exact
symbolic solutions you previously learned to obtain by hand, the numerical approximations you found using a calculator, and the graphs you have drawn. Maple can also carry out many computations and manipulations that would be extremely difficult to complete by hand. Maple is one of several CAS's; other major examples are Mathematica, Macsyma, Derive, and MathCad.
How will Maple be used in this course?
Our first, and largest, use of Maple will be the graphical display of functions. In fact, this graphical information is often more useful than a formula for the exact value of a problem. Sometimes we will use Maple just for demonstrations; other times I expect you will decide to turn to the computers to carry out caculations. This use of Maple is designed for the purpose of enhancing you understanding of calculus and your ability to formulate and solve (simple) problems by hand.
Note: You might find Maple of use in other courses!
Documentation and Online Help
The on-line help for Maple is very good. The help pages describe the syntax of each command, a brief description of the algorithm that has been implemented, and a few examples illustrating the use of the command. To obtain help on the command
func
, type:
?func
. To close a help window use the small button in the top right corner; to simply turn it into a small icon for later reference use the minimize button, also in the top right corner (this works for any window actually, and the box next to it opens a window up to full size). The Help Browser, an interactive interface to the entire Maple help system, can be brought up by clicking on
Help
, found at the top right of the Maple window.
Getting Started
When Maple starts, it knows nothing. Sometimes, after you have done some work, you want to reset Maple's memory to its original blank state. The first of the following commands does this; the second command loads a number of additional plotting routines that will be used in many examples.
Warning, the name changecoords has been redefined
Information about these commands can be found in the on-line help:
?plots
,
?restart
.
Basic Facts
Maple is a computer language; it cannot read your mind. You need to learn how to communicate with Maple.
The fundamental symbols:
-
a
ssignments are made with
:=
(plain
=
has a different meaning) -- think of this as giving the value of the right hand side to the name that appears on the left hand side
| > |
x := 1; # assignment
x + 1;
|

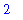
| > |
y = 1; # no assignment
y + 1;
|
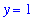
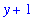
-
the unassign command should be used to remove an assignment from one or more specific names
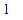
| > |
unassign( 'x' ); # the quote marks are required
x;
|
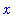
-
every command is terminated by a semi-colon (
;
) or colon (
:
) -- with the latter the computation is done, but the result is not displayed
-
the percent sign (
%
) refers to the result of the immediately preceding computation (use this rarely, if ever!)
-
Maple is case sensitive -- that is, the names
x
and
X
are different,
pi
,
Pi
, and
PI
are not the same thing
| > |
[ pi, Pi, PI ]; # two of these "look" the same, but
|
![[pi, Pi, PI]](images/lab017.gif)
| > |
map( evalf, % ); # only one is actually the constant
|
![[pi, 3.141592654, PI]](images/lab018.gif)
-
{ }
[ ]
-- set and list notation, respectively; the key difference is that lists are ordered and can have repeated elements
-
a .. b
-- this is how Maple indicates the interval
![[a, b]](images/lab019.gif) , that is, the real numbers from
, that is, the real numbers from
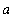 to
to
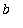
-
?
or
help
-- a request to Maple for information
The standard mathematical functions are denoted by their standard names:
+
(plus) ,
-
(minus) ,
*
(times) ,
/
(divided by) ,
^
(raised to the power) ,
sin
,
cos
,
tan
,
abs
,
sqrt
, ...
In the following lines, use paper and pencil to first predict what you think Maple will do. Then execute the command and see what actually happens!
| > |
number:= 4 * 6 + 12 / 6 - 1 ;
|
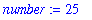
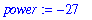
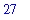

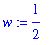
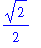
Error, (in tan) numeric exception: division by zero
| > |
3 / ( 5 - sqrt( number ) ) ;
|
Error, numeric exception: division by zero
Now enter some commands of your own! To produce the input prompt
>
use the
[>
button in the Menu Bar. Be generous with the space bar to make your commands easy to read, and to edit (modify after the fact). Go back to the tangent calculation above (remember how to reposition the cursor!) and change it to compute the tangent of
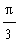 .
.
Next we define some functions to use for demonstrating Maple's graphing capabilities:
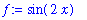
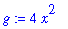
| > |
h:= 0.25 * cos ( 8 * x ) ;
|
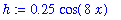

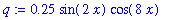
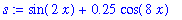
Plotting
Graphs of functions are produced by the
plot
command. In its simplest form,
plot
needs to know the function to be plotted and the range of values for the independent variable. Recall that
a..b
is Maple's way of describing the interval
![[a, b]](images/lab0125.gif) . Observe that I have placed titles on some of these graphs. When that any plot submitted with your lab report, MUST have axis labels and a title. (In fact, a legend should be included in most plots.) Again, try to predict the output before tapping the return key!
. Observe that I have placed titles on some of these graphs. When that any plot submitted with your lab report, MUST have axis labels and a title. (In fact, a legend should be included in most plots.) Again, try to predict the output before tapping the return key!
| > |
plot( 3 * t - 2 , t = -3 .. 10 ) ; # WAIT FOR THE GRAPH TO APPEAR!!
|
![[Maple Plot]](images/lab0126.gif)
| > |
plot( f , x = -Pi .. 2 * Pi, y = -1 .. 1 ) ;
|
![[Maple Plot]](images/lab0127.gif)
| > |
plot( p , x = -6 .. 8 , title = ` f * g ` );
|
![[Maple Plot]](images/lab0128.gif)
These plots are nice, but what information do they convey? Let's concentrate on the plot of p, that is f*g. Position the cursor on a point on the graph and click the left button. The numbers that appear on the upper-left corner of the Maple window are the coordinates of the current location of the cursor. Use this technique to identify the global maximum and minimum values of f*g on the interval [-6, 8], and the x-values at which these are found. Where do other (local) minima and maxima occur? Can you guess the exact values?
| > |
plot( 2 * u^3 + 4 * u - 5 , u = -10 .. 7 , title = ` cubic function ` ) ;
|
![[Maple Plot]](images/lab0129.gif)
Where does the cubic function cross the u-axis? Maybe it would be helpful to cut down the plotting interval from [-10, 7] to [-1, 3], or even narrower, say to [0, 1.5]. Try it. Can you find the u-intercept to 2-decimal point accuracy by this process? It is a powerful method, which we call ZOOMING IN.
| > |
plot( s , x = 0 .. 3 * Pi );
|
![[Maple Plot]](images/lab0130.gif)
| > |
plot( q , x = -1.2 .. 1.2 ) ;
|
![[Maple Plot]](images/lab0131.gif)
Can you explain why the graphs of s and q look the way they do?
Housecleaning
As you scroll up and down you may find that old plots take time to be redrawn and aren't really needed anyhow. If you click on a plot you will box it (and for printing purposes this box can be resized by dragging on the sides or corners). To remove it hold down the shift key and press delete.
Graphing Several Functions in One Plot
| > |
plot( [ p , g , -g ] , x= -6 .. 8, color=[red,blue,green], title="The Squeeze Theorem", legend=["y=p(x)","y=g(x)","y=-g(x)"] );
|
![[Maple Plot]](images/lab0132.gif)
| > |
plot( [ f , h , s ], x=0 .. 3*Pi, color=[red,blue,green], title="Plot of 2 trig functions and their sum", legend=["y=f(x)","y=h(x)","y=s(x) = f(x)+h(x)"] );
|
![[Maple Plot]](images/lab0133.gif)
Can you explain the little bumps that appear inside the large dips in the graph of s?
Plotting A Discontinuous Function
The tangent function is well-known to all of us. In particular, we know that the graph of
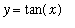 has vertical asymptotes at all odd multiples of
has vertical asymptotes at all odd multiples of
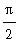 . Let's see how Maple handles this.
. Let's see how Maple handles this.

| > |
plot( f , x = -Pi .. Pi );
|
![[Maple Plot]](images/lab0137.gif)
The key is to restrict the vertical range of the plot and tell Maple that the function is discontinuous.
| > |
plot( f, x = -Pi .. Pi , y = -10 .. 10 );
|
![[Maple Plot]](images/lab0138.gif)
| > |
plot( f, x = -Pi .. Pi , y = -10 .. 10 , discont=true );
|
![[Maple Plot]](images/lab0139.gif)
| > |
plot ( ( 1 - 0.4*t^3) / ( 1 - t^2 ) , t = -3 .. 5 , -10 .. 10 ,
discont = true, title = `vertical asymptotes [by DM]` ) ;
|
![[Maple Plot]](images/lab0140.gif)
This technique is very useful for any function that has vertical asymptotes.
Calculus I - Limits, Derivatives, and Integrals
The natural logarithm function can be defined as a definite integral
| > |
LNx := Int( 1/t, t=1..x );
|
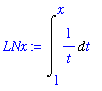
The
value
command can be used to confirm that this integral does represent the natural logarithm function:
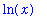
Further verification can be obtained from a plot of the function:
| > |
plot( LNx, x=0..10, title="My logarithm function" );
|
![[Maple Plot]](images/lab0143.gif)
The diff command is used to find derivatives:
| > |
diff( LNx, x ); # be sure to specify the variable
|
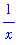
In Calculus I you probably encountered a limit problem similar to
| > |
F := sin(3*x)/sin(5*x): # note the use of :
L := Limit( F, x=0 );
|
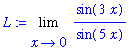
Maple can evaluate this limit:
| > |
L = value( L ); # note the use of = to create a nicely formatted result
|
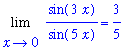
How is this limit evaluated? Direct substitution does not work because the denominator's limit (as x->0) is 0. The evaluation of this limit by hand requires two uses of the basic result
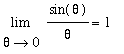 . (The details will not be presented here.) Visual confirmation of this value for the limit can be obtained from a plot:
. (The details will not be presented here.) Visual confirmation of this value for the limit can be obtained from a plot:
| > |
plot( F, x=-Pi..Pi, y=-15..15, discont=true ); # Zoom in to see the value of the limit
|
![[Maple Plot]](images/lab0148.gif)
Congratulations
You have just completed your first Maple worksheet. If you wish to save it select
File
in the menu bar, and then either
Save
(which will destroy the original version of day1.mws) or
Save As...
(which will leave day1.mws untouched, and will request a new name for this modified version). Worksheet names should always end with .mws; also unless you really need the output it is usually a good idea to remove it before saving -- to do this, select Edit, then Remove Output.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[a, b]](images/lab019.gif) , that is, the real numbers from
, that is, the real numbers from
 to
to
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/lab0126.gif)
![[Maple Plot]](images/lab0127.gif)
![[Maple Plot]](images/lab0128.gif)
![[Maple Plot]](images/lab0129.gif)
![[Maple Plot]](images/lab0130.gif)
![[Maple Plot]](images/lab0131.gif)
![[Maple Plot]](images/lab0132.gif)
![[Maple Plot]](images/lab0133.gif)
![[Maple Plot]](images/lab0137.gif)
![[Maple Plot]](images/lab0138.gif)
![[Maple Plot]](images/lab0139.gif)
![[Maple Plot]](images/lab0140.gif)
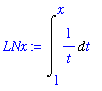
![[Maple Plot]](images/lab0143.gif)
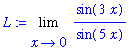
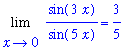
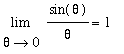 . (The details will not be presented here.) Visual confirmation of this value for the limit can be obtained from a plot:
. (The details will not be presented here.) Visual confirmation of this value for the limit can be obtained from a plot:
![[Maple Plot]](images/lab0148.gif)