The point P and the curves Q and R 

>	P := r -> [ 0, 0, r ];

 

>

 

>	Qr := (r,a) -> r*sqrt(4*a^2-r^2)/2/a:

 

>	Qx := Qr(r,a)*cos(theta):

 

>	Qy := r^2/2/a:

 

>	Qz := Qr(r,a)*sin(theta):

 

>	Q := unapply( [ Qx, Qy, Qz ], [theta,r,a] );

 

>

 

>	Rr := (r,a) -> sqrt( 4*a^2-r^2 ):

 

>	Rx := r*sqrt(4*a^2-r^2)*cos(theta)/(2*a-sqrt(4*a^2-r^2)*sin(theta)):

 

>	Ry := r^2                         /(2*a-sqrt(4*a^2-r^2)*sin(theta)):

 

>

Rz := 0:

 

>	R := unapply( [ Rx, Ry, Rz ], [theta,r,a] );

 

>

 

Plotting routines 

Animations 

>	anim1  := (r,a,n) -> animate( plotPQR, [ theta, r, a ], theta=0..2*Pi, frames=n, background=P1(r,a,n),  args[4..-1] ):

 

>	anim1p := (r,a,n) -> animate( plotPQR, [ theta, r, a ], theta=0..2*Pi, frames=n, background=P1p(r,a,n), args[4..-1] ):

 

>

 

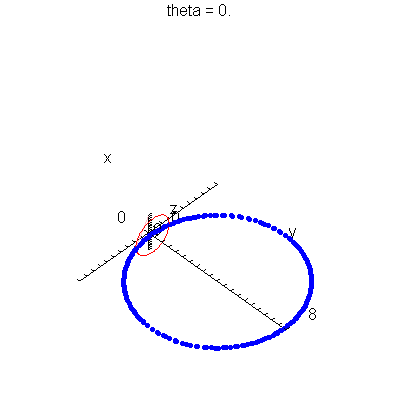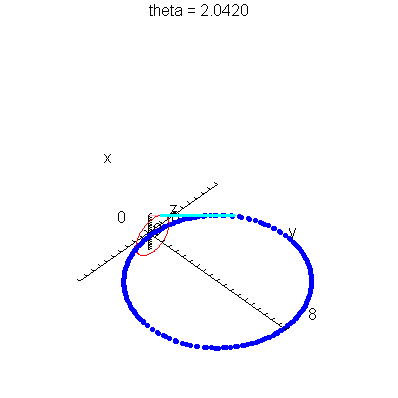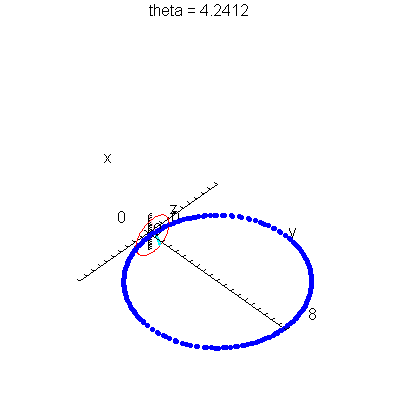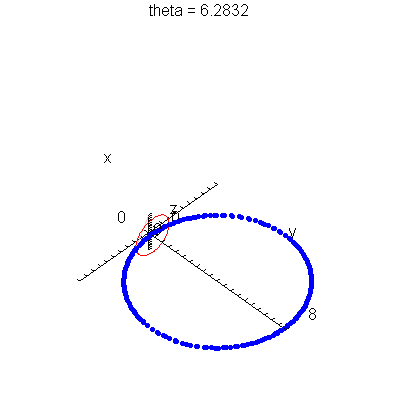
>	anim1p( 1, 1, 21, scaling=constrained ); # circles Q and R plotted as discrete samples of points

 

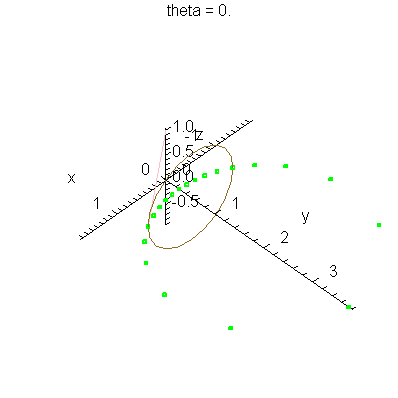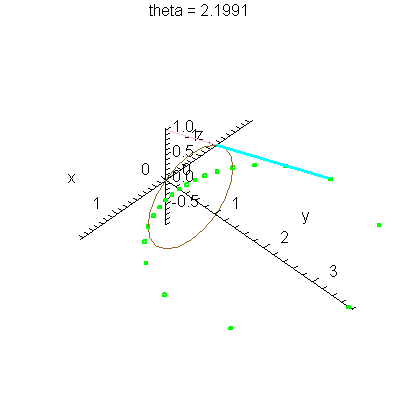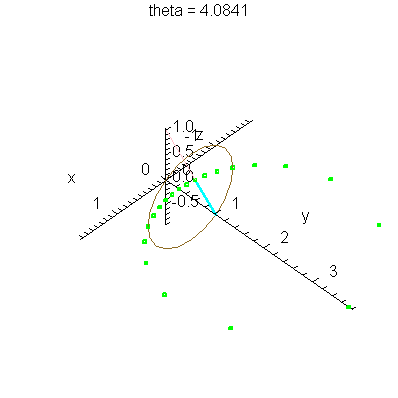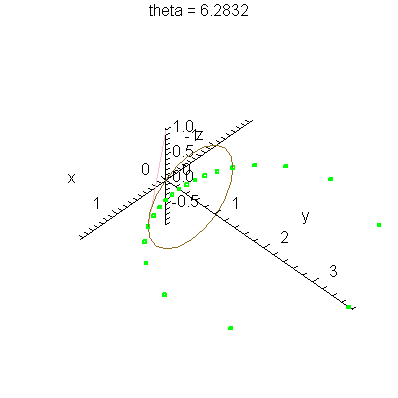
>	anim1( 1, 1, 21, scaling=constrained );  # circles Q and R plotted as circles

 

>

 

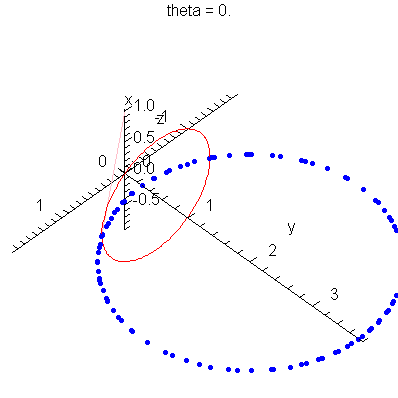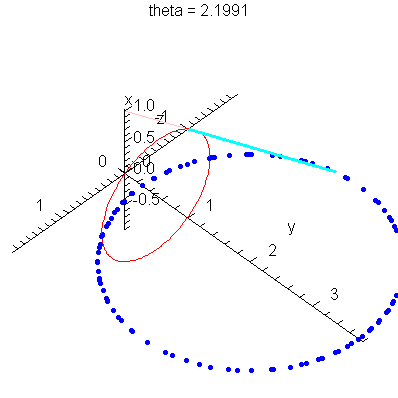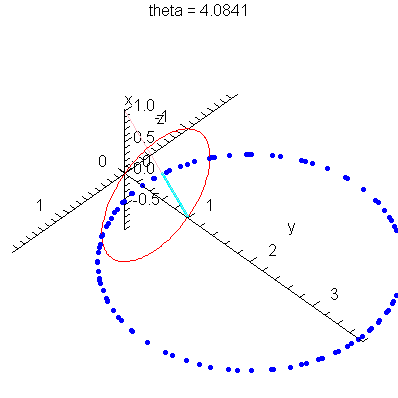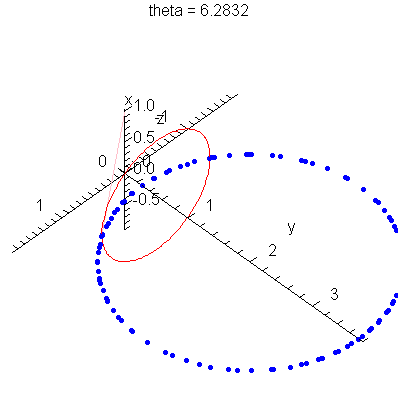
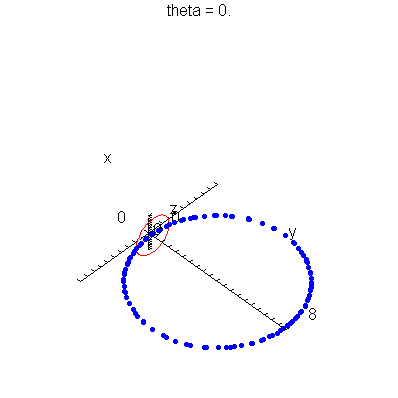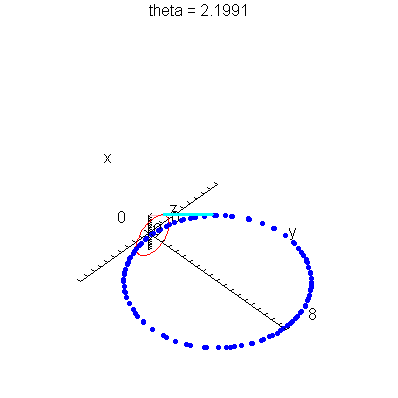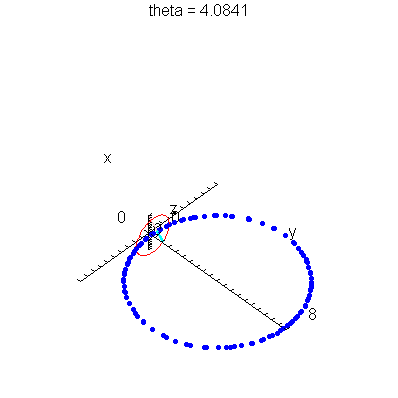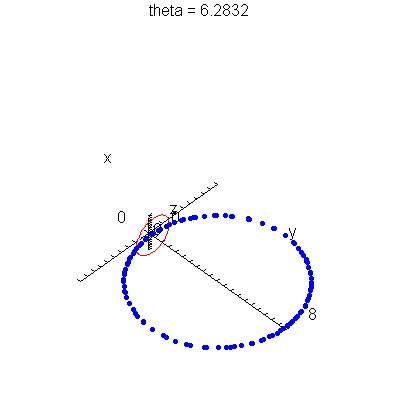
>	anim1p( 1, 2, 21, scaling=constrained ); # circles Q and R plotted as discrete samples of points

 

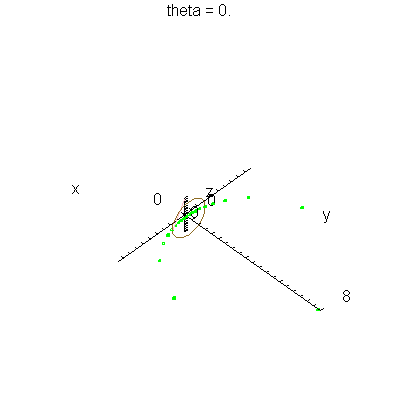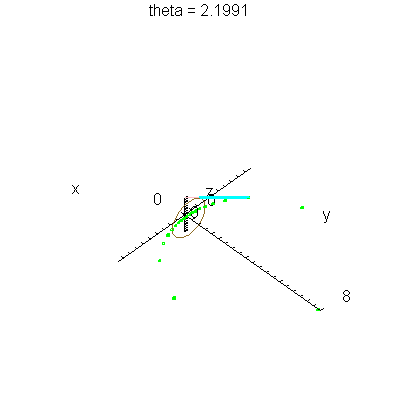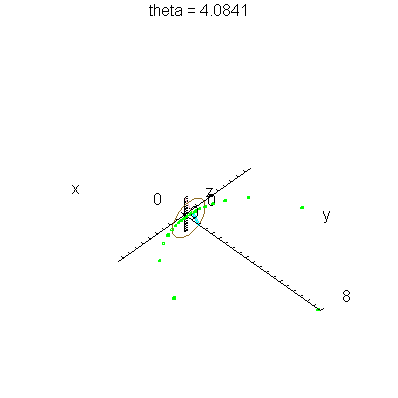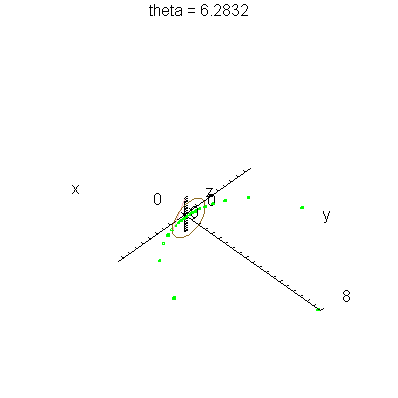
>	anim1( 1, 2, 21, scaling=constrained );  # circles Q and R plotted as circles

 

>

 

>	anim1p( 1, 2, 41, scaling=constrained ); # circles Q and R plotted as discrete samples of points

 

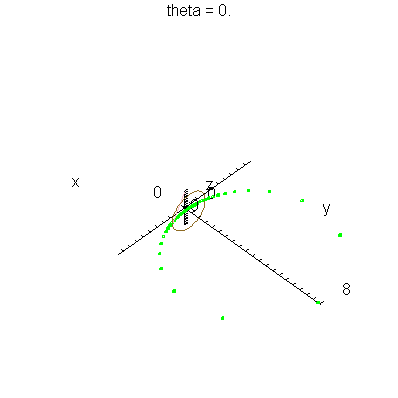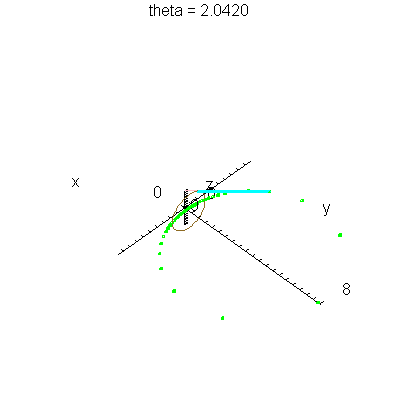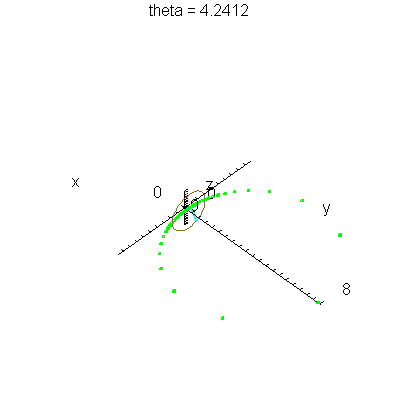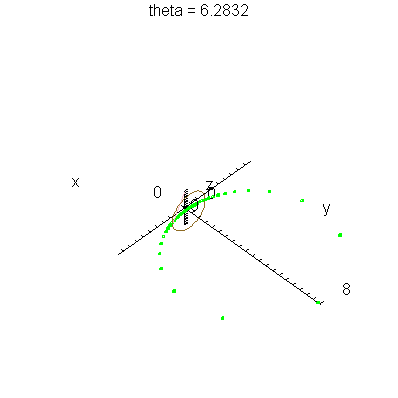
>	anim1( 1, 2, 41, scaling=constrained );  # circles Q and R plotted as circles

 

>

 

>