Length.mws
Length of a Plane Curve
| > |
restart;
with( plots ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Auxiliary Plotting Procedures (do not modify)
| > |
Ptriangle := display(
plot( [[1,1],[3,6]], style=point, color=blue ),
plot( [[1,1],[3,6]], color=red, linestyle=DOT ),
plot( [[1,1],[3,1],[3,6]], color=pink ),
textplot( [0.8,0.8,"A"],align={below,left} ),
textplot( [3.2,6.2,"B"],align={above,right} ),
textplot( [2,0.8,"D"],align={below},font=[SYMBOL,12] ),
textplot( [2.2,0.8,"x"],align={below} ),
textplot( [3.2,3.5,"D"],align={right},font=[SYMBOL,12] ),
textplot( [3.4,3.5,"y"],align={right} ),
scaling=constrained, axes=none ):
|
| > |
ArcLengthApprox := proc( f, domain, N )
local x, a, b, F, frames, ArcLengthApproxFrame;
x,a,b := lhs(domain),op(rhs(domain));
if type(f,procedure) then
F:=f
else
F:=unapply(f,x)
end if;
ArcLengthApproxFrame := proc( F, a, b, N )
local Xpt, XYpt, XY2pt, P0, P1, P2;
Xpt := [ (b-a)*i/N $ i=0..N ];
XYpt := [ seq( [X,F(X)], X=Xpt ) ];
XY2pt := [ seq( op([[Xpt[i],F(Xpt[i])],[Xpt[i+1],F(Xpt[i])]]),
i=1..N ),
[Xpt[N+1],F(Xpt[N+1])] ];
P0 := plot( F(x), x=a..b, linestyle=DOT, legend="curve: C" );
P1 := plot( [ XYpt$2 ], style=[point,line], color=blue, legend=["points",""] );
P2 := plot( XY2pt, color=pink, legend="line segments" );
return display( P0,P1,P2, title=sprintf("Arclength Approximation\nwith n=%a Subintervals", N) );
end proc;
if type(N,posint) then
return ArcLengthApproxFrame( F, a, b, N )
else
frames := seq( ArcLengthApproxFrame( F, a, b, n ), n=N );
return display( [frames], insequence=true )
end if;
end proc:
|
Lesson Overview
The length of a curve in the plane is also known as the arclength of the curve. For a curve with bends and twists this one-dimensional geometric quantity can be difficult to measure directly. The length of straight segments, however, are easy to compute. The length of the line segment between two points A = (
![x[1]](images/Length1.gif) ,
,
![y[1]](images/Length2.gif) ) and B = (
) and B = (
![x[2]](images/Length3.gif) ,
,
![y[2]](images/Length4.gif) ) can be found (by the Pythagorean Theorem) to be
) can be found (by the Pythagorean Theorem) to be
![L[AB] = sqrt((Delta*x)^2+(Delta*y)^2)](images/Length5.gif)
![[Maple Plot]](images/Length6.gif)
where the horizontal distance between the points (or run) is
![Delta*x = x[2]-x[1]](images/Length7.gif) and the vertical difference between the two points (or rise) is
and the vertical difference between the two points (or rise) is
![Delta*y = y[2]-y[1]](images/Length8.gif) .
.
For a curved path, C, the idea is to divide the curve into short segments. If the curve does not have corners or cusps, and if the pieces are short enough, then the each curved segment can be approximated by a line segment. Adding the lengths of these line segments will approximate the length of the curved path; in the limit this will yield the length of the curve. That is:
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length9.gif) .
.
The special Maple command,
ArcLengthApprox
, defined at the top of this worksheet can present an animation showing how the short segments approximate the curved path as the number of segments increases.
| > |
ArcLengthApprox( x/2+sin(x), x=0..20, [5,10,20,40,80] );
|
![[Maple Plot]](images/Length10.gif)
The general process appears to be very similar to the slice, approximate, limit, evaluate procedure used in other applications of the definite integral. The only problem is that the sum does not look like a
Riemann Sum.
Special Case 1:
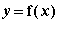
If the curve is the graph of a differentiable function
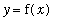 on the interval
on the interval
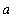 <=
<=
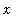 <=
<=
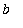 , then
, then
![Delta*y[i] = y[i]-y[i-1]](images/Length16.gif)
![`` = f(x[i])-f(x[i-1])](images/Length17.gif)
![`` = `f '`(x[i]^`*`)*(x[i]-x[i-1])](images/Length18.gif) by the
Mean Value Theorem (for Derivatives)
by the
Mean Value Theorem (for Derivatives)
![`` = `f '`(x[i]^`*`)*Delta*x[i]](images/Length19.gif)
where
![x[i]^`*`](images/Length20.gif) is some number between
is some number between
![x[i-1]](images/Length21.gif) and
and
![x[i]](images/Length22.gif) . (Note that the
Mean Value Theorem is applicable only because we assumed the function is differentiable.) When this is substituted into the general arclength formula and simplified, the sum is recognized as a Riemann sum and the arclength can be expressed as a definite integral:
. (Note that the
Mean Value Theorem is applicable only because we assumed the function is differentiable.) When this is substituted into the general arclength formula and simplified, the sum is recognized as a Riemann sum and the arclength can be expressed as a definite integral:
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length23.gif)
![`` = Limit(Sum(sqrt((Delta*x[i])^2+(`f '`(x[i]^`*`)*Delta*x[i])^2),i = 1 .. n),n = infinity)](images/Length24.gif)
![`` = Limit(Sum(sqrt(1+`f '`(x[i]^`*`)^2)*Delta*x[i],i = 1 .. n),n = infinity)](images/Length25.gif)
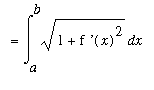 .
.
Special Case 2:
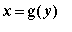
Similarly, if the curve is the graph of a differentiable function
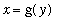 on the interval
on the interval
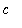 <=
<=
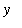 <=
<=
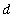 , then the
Mean Value Theorem (for Derivatives) can be used to write
, then the
Mean Value Theorem (for Derivatives) can be used to write
![Delta*x[i] = `g'`(y[i]^`*`)*Delta*y[i]](images/Length32.gif) where
where
![y[i]^`*`](images/Length33.gif) is a number between
is a number between
![y[i-1]](images/Length34.gif) and
and
![y[i]](images/Length35.gif) . Then, we obtain
. Then, we obtain
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length36.gif)
![`` = Limit(Sum(sqrt((`g'`(x[i]^`*`)*Delta*y[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length37.gif)
![`` = Limit(Sum(sqrt(`g'`(y[i]^`*`)^2+1)*Delta*y[i],i = 1 .. n),n = infinity)](images/Length38.gif)
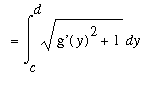 .
.
Special Case 3: Parametric Form
The third case is a generalization of the previous cases. Suppose the points on the curve can be described in terms of a pair of parametric equations:
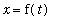 ,
,
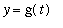 ,
,
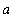 <=
<=
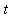 <=
<=
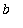 .
.
This means that the curve begins at the point (
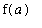 ,
,
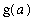 ), passes through all points (
), passes through all points (
 ,
,
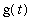 ) in order as
) in order as
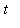 increases from
increases from
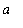 to
to
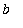 , and terminates at the point (
, and terminates at the point (
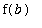 ,
,
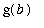 ). For example, the line segment from ( 1, 2 ) to ( 3, 0 ) can be given in parametric form as
). For example, the line segment from ( 1, 2 ) to ( 3, 0 ) can be given in parametric form as
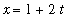 ,
,
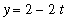 for 0 <=
for 0 <=
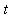 <= 1. The
animatecurve
command from the
plots
package presents a very nice picture of a parametric curve as the parameter increases throughout its domain:
<= 1. The
animatecurve
command from the
plots
package presents a very nice picture of a parametric curve as the parameter increases throughout its domain:
| > |
animatecurve( [1+2*t,2-2*t,t=0..1],
view=[0..4,0..3],
title="Line Segment in Parametric Form" );
|
![[Maple Plot]](images/Length57.gif)
One parameterization of the unit circle is
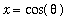 ,
,
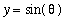 for 0 <=
for 0 <=
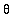 <
<
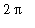 .
.
| > |
animatecurve( [cos(theta),sin(theta),theta=0..2*Pi],
scaling=constrained,
title="Unit Circle in Parametric Form" );
|
![[Maple Plot]](images/Length62.gif)
Notes about parametric curves
-
To plot a parametric curve without animation, change
animatecurve
to
plot
.
-
There are many parametric forms for the same curve.
If the both functions f and g are continuous on [
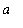 ,
,
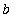 ] and differentiable on (
] and differentiable on (
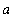 ,
,
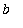 ) then the
Mean Value Theorem (for Derivatives) can be applied to both
) then the
Mean Value Theorem (for Derivatives) can be applied to both
![Delta*x[i]](images/Length67.gif) and
and
![Delta*y[i]](images/Length68.gif) . to obtain
. to obtain
![Delta*x[i] = `f '`(t[i]^`*`)*Delta*t[i]](images/Length69.gif) where
where
![t[i-1]](images/Length70.gif) <
<
![t[i]^`*`](images/Length71.gif) <
<
![t[i]](images/Length72.gif)
and
![Delta*y[i] = `g'`(t[i]^`^`)*Delta*t[i]](images/Length73.gif) where
where
![t[i-1]](images/Length74.gif) <
<
![t[i]^`^`](images/Length75.gif) <
<
![t[i]](images/Length76.gif)
Thus,
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length77.gif)
![`` = Limit(Sum(sqrt((`f '`(t[i]^`*`)*Delta*t[i])^2+(`g'`(t[i]^`^`)*Delta*t[i])^2),i = 1 .. n),n = infinity)](images/Length78.gif)
![`` = Limit(Sum(sqrt(`f'`(t[i]^`*`)^2+`g'`(t[i]^`^`)^2)*Delta*t[i],i = 1 .. n),n = infinity)](images/Length79.gif)
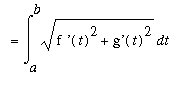 .
.
Note that there is no reason to expect
![t[i]^`*` = t[i]^`^`](images/Length81.gif) and so the final sum is not a
Riemann Sum. Using techniques well beyond the scope of this course it can be shown that -- in the limit -- this is not important and the definite integral does give the arclength of a parametric curve.
and so the final sum is not a
Riemann Sum. Using techniques well beyond the scope of this course it can be shown that -- in the limit -- this is not important and the definite integral does give the arclength of a parametric curve.
General Comments about Arclength
-
If a curve has a corner or cusp, compute the arclength of each smooth section and add the results.
-
For most arclength problems, the definite integrals cannot be evaluated in terms of elementary functions.
-
The
ArcLength
maplet [
Maplet Viewer][
MapleNet] provides a convenient interface for visualizing and computing arclength when the curve can be written as
 for
for
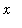 in an interval, i.e., for Special Case 1..
in an interval, i.e., for Special Case 1..
Example 1: Plane Curve with
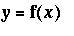
Find the arclength of the curve
| > |
f1 := (x^4+3)/(6*x):
y = f1;
|
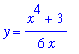
between
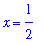
and
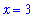
| > |
plot( f1, x=lo1..hi1, view=[0..3,0..4] );
|
![[Maple Plot]](images/Length88.gif)
According to the arclength formula for a curve given by y=f(x), the length of this curve is given by a defniite integral with integrand
| > |
q1 := sqrt( diff( f1, x )^2 + 1 ):
q1;
|
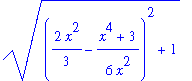
In this form there is no hope of finding an antiderivative. But, if the inner expression is expanded and simplified (with appropriate assumptions on x)
| > |
q2 := expand( q1 ):
q3 := simplify( q2 ):
q4 := simplify( q3 ) assuming x>1:
ds1 := expand( q4 ):
q1 = q2;
`` = q3;
`` = q4;
`` = ds1;
|
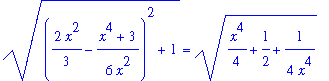
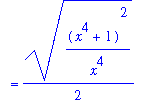
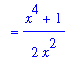
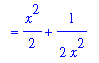
This function will not be difficult to integrate! The definite integral for the length of this curve is
| > |
L1 := Int( ds1, x=lo1..hi1 ):
L = L1;
`` = value( L1 );
|
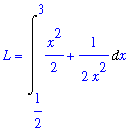
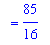
The same results can be obtained with the
ArcLength
maplet [
Maplet Viewer][
MapleNet] or with the
ArcLength
command from the
Student[Calculus1]
package:
| > |
q5 := ArcLength( f1, lo1..hi1, output=integral ):
L = q5;
`` = value( q5 );
|
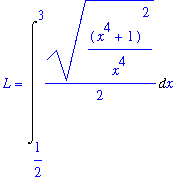
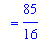
Concluding Remark
Observe that this example could not be treated as a plane curve in the form
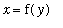 because the function is not 1-1 on the interval [
because the function is not 1-1 on the interval [
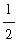 , 3 ].
, 3 ].
Example 2: Plane Curve with
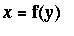
Find the length of the curve
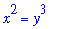
between the points ( 1, 1 ) and ( 8, 4 ).
| > |
implicitplot( F2, x=1..8, y=1..4, scaling=constrained );
|
![[Maple Plot]](images/Length102.gif)
Because this curve is so linear, a quick lower bound for the arclength is the distance between the endpoints:
| > |
d2 := sqrt( (8-1)^2 + (4-1)^2 ):
L[est] = d2;
`` = evalf( d2 );
|
![L[est] = 58^(1/2)](images/Length103.gif)

This curve passes the horizontal and vertical line tests; it can be written either as
y = x^(3/2) for 1 < x < 4 or as x = y^(2/3) for 1 < y < 8. Let's pursue the latter option.
| > |
f2x := rhs( isolate( F2=0, y ) ):
y = f2x;
|
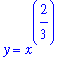
for x in
| > |
lo2x := 1:
hi2x := 8:
lo2x .. hi2x;
|
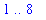
or as
| > |
f2y := rhs( isolate( F2=0, x ) ):
x = f2y;
|
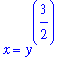
for y in
| > |
lo2y := 1:
hi2y := 4:
lo2y .. hi2y;
|
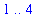
Attempting to use the first form involves the integrand
| > |
sqrt( diff( f2x, x )^2 + 1 );
|
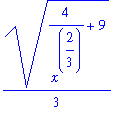
The prospects for finding an antiderivative of this function are slim. And, further manipulations of this expression do not improve the situation. Let's see if the integrand for the second form is any better (or worse):
| > |
ds2 := sqrt( 1 + diff( f2, y )^2 ):
ds2;
|
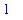
It is easy to find an antiderivative of this function. Continuing to work towards our goal of finding the length of this curve with this representation leads to the definite integral
| > |
L2 := Int( ds2, y=lo2y..hi2y ):
L = L2;
`` = value( L2 );
`` = evalf( value( L2 ) );
|
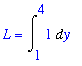
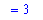
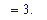
Note that this result is, as expected, slightly larger than the distance between the endpoints.
This example shows how the arclength can be computed easily in one form and is almost impossible to compute (explicitly) with other representations.
Example 3: Plane Curve in Parametric Form
Consider the parametric curve given by
| > |
f3 := sqrt(5)*sin(2*t)-2:
g3 := sqrt(5)*cos(2*t)-sqrt(3):
lo3 := 0:
hi3 := Pi/2:
x = f3; y = g3; t = lo3..hi3;
|
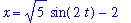
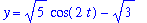
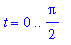
According to the general analysis earlier in this lesson, the integrand for the arclength integral will be
| > |
q1 := sqrt( diff(f3,t)^2 + diff(g3,t)^2 ):
|
| > |
ds3 := simplify( q1 ):
q1 = ds3;
|

This could not be much simpler to integrate. The resulting (trivial) definite integral for the arclength of this curve is
| > |
L3 := Int( ds3, t=0..Pi/2 ):
L = L3;
`` = value( L3 );
|
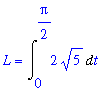
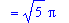
What is this curve and why did the problem simplify so nicely? To answer the first question, recall the discussion of the
animatecurve
command from the
plots
package.
| > |
animatecurve( [f3,g3,t=lo3..hi3], view=[-5..1,-5..1], scaling=constrained );
|
![[Maple Plot]](images/Length120.gif)
Aha! This is appears to be a semicircle. The center is (2, sqrt(3) ) and the radius is sqrt(5). From geometry, the circumference of a semicircle with radius sqrt(5) is Pi*sqrt(5), exactly the value found above via Calculus.
Lesson Summary
The slice, approximate, limit, evaluate procedure has been used, once again, to develop definite integrals for three general classes of curves. The
Mean Value Theorem for Derivatives plays a fundamental role in the identification of the approximating sum as a
Riemann Sum. Without this key piece of knowledge there would be no general method for expressing arclength as a definite integral.
The
ArcLengthApprox
command (defined at the beginning of this worksheet) can prepare an animation showing how a curved path can be approximated by a piecewise linear approximating function. The
ArcLength
maplet [
Maplet Viewer][
MapleNet] can be used to check that the definite integral has been correctly formulated and evaluated (exactly and numerically).
What's Next?
The emphasis of this application is setting up the definite integral. Evaluating the integral to find a numeric (or symbolic) expression for the volume is important but this is a secondary concern. The
online homework assignment, including the practice sessions, emphasize the conceptual topics of this lesson.. Work enough practice problems to master these concepts, then complete the online homework assignment and the
assigned problems from the text. The textbook problems typically involve both the setup of the definite integral and its evaluation.
The
online homework assignment for arclength provides practice applying the concepts and ideas introduced in this lesson. As with other lessons in this unit, concepts are emphasized more than computations. Use the practice sessions to hone your skills, then attempt the online graded homework assignment. The
assigned problems from the text ask that you evaluate the integral as well. Remember to look for simplifications to the integrand before you spend too much time trying to evaluate an arclength integral.
The final lesson in this unit introduces
Work as applications of definite integral.
![]() ,
,
![]() ) and B = (
) and B = (
![]() ,
,
![]() ) can be found (by the Pythagorean Theorem) to be
) can be found (by the Pythagorean Theorem) to be
![L[AB] = sqrt((Delta*x)^2+(Delta*y)^2)](images/Length5.gif)
![[Maple Plot]](images/Length6.gif)
![]() and the vertical difference between the two points (or rise) is
and the vertical difference between the two points (or rise) is
![]() .
.
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length9.gif) .
.
![[Maple Plot]](images/Length10.gif)
![]()
![]() on the interval
on the interval
![]() <=
<=
![]() <=
<=
![]() , then
, then
![]()
![]()
![]() by the
Mean Value Theorem (for Derivatives)
by the
Mean Value Theorem (for Derivatives)![]()
![]() is some number between
is some number between
![]() and
and
![]() . (Note that the
Mean Value Theorem is applicable only because we assumed the function is differentiable.) When this is substituted into the general arclength formula and simplified, the sum is recognized as a Riemann sum and the arclength can be expressed as a definite integral:
. (Note that the
Mean Value Theorem is applicable only because we assumed the function is differentiable.) When this is substituted into the general arclength formula and simplified, the sum is recognized as a Riemann sum and the arclength can be expressed as a definite integral:
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length23.gif)
![`` = Limit(Sum(sqrt((Delta*x[i])^2+(`f '`(x[i]^`*`)*Delta*x[i])^2),i = 1 .. n),n = infinity)](images/Length24.gif)
![`` = Limit(Sum(sqrt(1+`f '`(x[i]^`*`)^2)*Delta*x[i],i = 1 .. n),n = infinity)](images/Length25.gif)
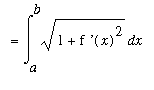 .
.
![]()
![]() on the interval
on the interval
![]() <=
<=
![]() <=
<=
![]() , then the
Mean Value Theorem (for Derivatives) can be used to write
, then the
Mean Value Theorem (for Derivatives) can be used to write
![]() where
where
![]() is a number between
is a number between
![]() and
and
![]() . Then, we obtain
. Then, we obtain
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length36.gif)
![`` = Limit(Sum(sqrt((`g'`(x[i]^`*`)*Delta*y[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length37.gif)
![`` = Limit(Sum(sqrt(`g'`(y[i]^`*`)^2+1)*Delta*y[i],i = 1 .. n),n = infinity)](images/Length38.gif)
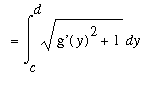 .
.
![]() ,
,
![]() ,
,
![]() <=
<=
![]() <=
<=
![]() .
.
![]() ,
,
![]() ), passes through all points (
), passes through all points (
![]() ,
,
![]() ) in order as
) in order as
![]() increases from
increases from
![]() to
to
![]() , and terminates at the point (
, and terminates at the point (
![]() ,
,
![]() ). For example, the line segment from ( 1, 2 ) to ( 3, 0 ) can be given in parametric form as
). For example, the line segment from ( 1, 2 ) to ( 3, 0 ) can be given in parametric form as
![]() ,
,
![]() for 0 <=
for 0 <=
![]() <= 1. The
animatecurve
command from the
plots
package presents a very nice picture of a parametric curve as the parameter increases throughout its domain:
<= 1. The
animatecurve
command from the
plots
package presents a very nice picture of a parametric curve as the parameter increases throughout its domain:
![[Maple Plot]](images/Length57.gif)
![]() ,
,
![]() for 0 <=
for 0 <=
![]() <
<
![]() .
.
![[Maple Plot]](images/Length62.gif)
![]() ,
,
![]() ] and differentiable on (
] and differentiable on (
![]() ,
,
![]() ) then the
Mean Value Theorem (for Derivatives) can be applied to both
) then the
Mean Value Theorem (for Derivatives) can be applied to both
![]() and
and
![]() . to obtain
. to obtain
![]() where
where
![]() <
<
![]() <
<
![]()
![]() where
where
![]() <
<
![]() <
<
![]()
![L[C] = Limit(Sum(sqrt((Delta*x[i])^2+(Delta*y[i])^2),i = 1 .. n),n = infinity)](images/Length77.gif)
![`` = Limit(Sum(sqrt((`f '`(t[i]^`*`)*Delta*t[i])^2+(`g'`(t[i]^`^`)*Delta*t[i])^2),i = 1 .. n),n = infinity)](images/Length78.gif)
![`` = Limit(Sum(sqrt(`f'`(t[i]^`*`)^2+`g'`(t[i]^`^`)^2)*Delta*t[i],i = 1 .. n),n = infinity)](images/Length79.gif)
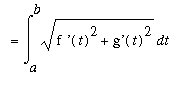 .
.
![]() and so the final sum is not a
Riemann Sum. Using techniques well beyond the scope of this course it can be shown that -- in the limit -- this is not important and the definite integral does give the arclength of a parametric curve.
and so the final sum is not a
Riemann Sum. Using techniques well beyond the scope of this course it can be shown that -- in the limit -- this is not important and the definite integral does give the arclength of a parametric curve.
 for
for
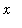 in an interval, i.e., for Special Case 1..
in an interval, i.e., for Special Case 1..
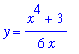
![[Maple Plot]](images/Length88.gif)
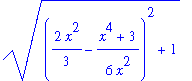
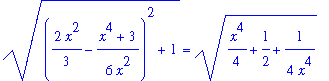
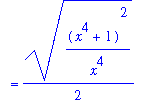
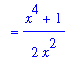
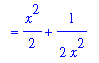
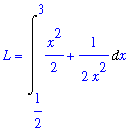
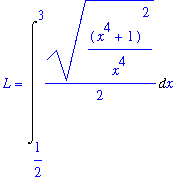
![[Maple Plot]](images/Length102.gif)
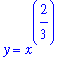
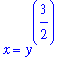
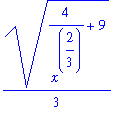
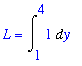
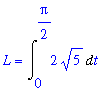
![[Maple Plot]](images/Length120.gif)