EvaluateDefInt.mws
Evaluating Definite Integrals
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
This lesson could be the first lesson in the
Applications of the Definite Integral unit. It is included here as a way to obtain additional practice with the evaluation of definite integrals. The main new technique that will be introduced is the Method of Substitution; an integral form for the
Chain Rule.
The examples provide a variety of different integration problems. General problems involving representative integrands for definite (and indefinite) integrals, generic even and odd functions, and the derivation of an antiderivative of
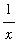 and properties of this antiderivative are discussed in detail.
and properties of this antiderivative are discussed in detail.
Remember to use the
Integration
maplet [
Maplet Viewer][
Maplenet] to help develop your integration skills.
Method of Substitution
Recall the Chain Rule (from the
Differentiation Rules lesson): If
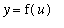 and
and
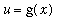 , where f and g are both differentiable functions, then
, where f and g are both differentiable functions, then
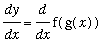 =
=
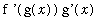 .
.
The integral form of this result is:
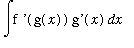 =
=
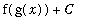 .
.
Of course, for a definite integral the
Second Fundamental Theorem of Calculus provides:
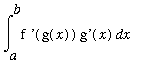 =
=
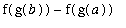 .
.
The key is to identify the integrand as the product of an expression that involves
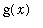 and the derivative
and the derivative
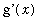 . In practice, one typically rewrites the integrand using the substitution
. In practice, one typically rewrites the integrand using the substitution
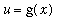 and replacing the differential
and replacing the differential
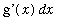 with
with
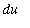 :
:
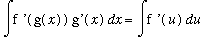 .
.
This puts the integral in a form where it is easy to identify an antiderivative:
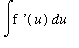 =
=
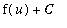 .
.
All that remains is to use the substitution to rewrite the antiderivative in terms of the original independent variable:
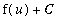 =
=
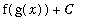 .
.
When the same steps are repeated for a definite integral the method can be written as
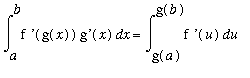 =
=
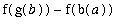 .
.
Example 1: Indefinite Integral
Evaluate the indefinite integral
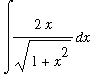 .
.
In the integrand notice that the numerator
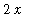 is the derivative of
is the derivative of
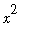 . While
. While
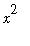 does appear elsewhere in the intgrand this observation is not immediately useful as an antiderivative of
does appear elsewhere in the intgrand this observation is not immediately useful as an antiderivative of
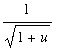 is not immediately known. But,
is not immediately known. But,
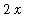 is also the derivative of
is also the derivative of
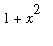 and an antiderivative of
and an antiderivative of
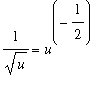 is known
is known
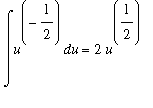 .
.
To put this together to complete the evaluation of this indefinite integral with the Method of Substitution:
Let
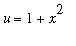 .
.
Then
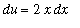 and
and
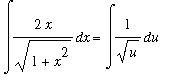
=
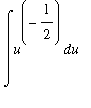
=
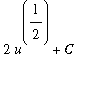
=
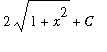 .
.
As with any indefinite integral, this answer can be checked:
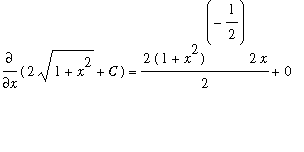
=
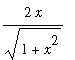 .
.
The fact that the derivative of the general antiderivative is the original integrand means that the computation has been done correctly.
Solution using the
Integration
maplet [
Maplet Viewer][
Maplenet]
The
Integration
maplet [
Maplet Viewer][
Maplenet] can be used to help find the antiderivative in this problem. Once the maplet is launched enter
2*x/sqrt(1+x^2)
in the
Function
field and
x
in the
Variable
field (as this is an indefinite integral, leave the
from
and
to
fields empty).
Click the
Start
button. To see the effect of trying the substitution
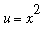 , enter
u=x^2
, u in the large box to the right of the
Rewrite
and
Change
buttons, then click
Change
. The
Problem Status
window will show that this substitution converts the integral to
, enter
u=x^2
, u in the large box to the right of the
Rewrite
and
Change
buttons, then click
Change
. The
Problem Status
window will show that this substitution converts the integral to
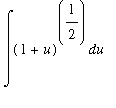 . As this is not a form for any of our known antiderivatives, this is a deadend for us.
. As this is not a form for any of our known antiderivatives, this is a deadend for us.
To restart the problem, click the
Start
button. To see the effect of trying the substitution
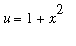 , enter
u=1+x^2, u
in the large box to the right of the
Rewrite
and
Change
buttons, then click
Change
. The
Problem Status
window will show that this substitution converts the integral to
, enter
u=1+x^2, u
in the large box to the right of the
Rewrite
and
Change
buttons, then click
Change
. The
Problem Status
window will show that this substitution converts the integral to
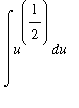 --- success! Click the
Power
button to have the
Power Rule applied. After this step the indefinite integral is evaluated as
--- success! Click the
Power
button to have the
Power Rule applied. After this step the indefinite integral is evaluated as
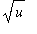 . To complete the evaluation of the indefinite integral it is necessary to undo the substitution; to do this click the
Revert
button. When writing the answer on paper do not forget to add the constant of integration.
. To complete the evaluation of the indefinite integral it is necessary to undo the substitution; to do this click the
Revert
button. When writing the answer on paper do not forget to add the constant of integration.
Note
If you ask the
Integration
maplet to show All Steps in the evaluation of this integral the results will be different from --- but ultimately equivalent to --- what has been discussed in this lesson.
Example 2: Definite Integral
Evaluate the definite integral
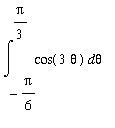 .
.
The only form of the cosine function that has a known antiderivative is
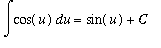 . In order to put the given integral in a form where this can be used, let
. In order to put the given integral in a form where this can be used, let
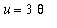 . Then
. Then
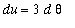 . While there is no factor in the integrand that matches the coefficient of 3 in the equation for the differentials, it is possible to replace
. While there is no factor in the integrand that matches the coefficient of 3 in the equation for the differentials, it is possible to replace
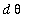 with
with
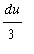 as follows:
as follows:
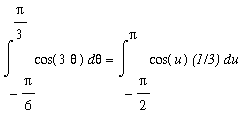
=
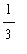
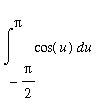
=
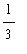 (
(
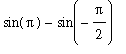 )
)
=
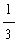 (
(
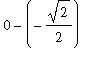 )
)
=
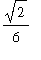 .
.
Notice that implicit in this work is the result of the indefinite integral:
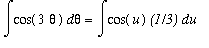
=
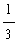 Int( cos(u), u )
Int( cos(u), u )
=
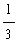
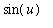 +
+
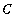
=
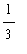
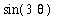 + C
+ C
and the definite integral can be evaluated using the Second Fundamental Theorem of Calculus:
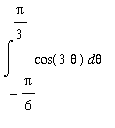 =
=
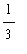
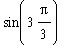 -
-
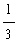
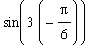 )
)
=
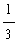
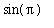 -
-
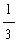
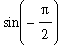
= 0 -
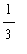 (
(
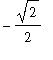 )
)
=
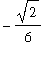
Example 3: Odd Function on a Symmetric Interval
Recall that an odd function is a function with the property that
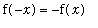 . An odd function is said to be symmetric about the origin. When an odd function is integrated over a symmetric interval [
. An odd function is said to be symmetric about the origin. When an odd function is integrated over a symmetric interval [
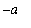 ,
,
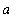 ] (
] (
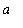 > 0 ) the value of the integral can be simplified. Suppose that
> 0 ) the value of the integral can be simplified. Suppose that
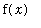 > 0 for
> 0 for
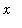 > 0. Then, by symmetry, the "area" under the curve on the interval [
> 0. Then, by symmetry, the "area" under the curve on the interval [
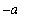 , 0 ] is the negative of the area under the curve on the interval [ 0,
, 0 ] is the negative of the area under the curve on the interval [ 0,
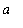 ].
].
| > |
P1 := plot( x+sin(3*x), x=-Pi..0, filled=true, color=cyan ):
P2 := plot( x+sin(3*x), x= 0..Pi, filled=true, color=pink ):
display( P1,P2, title="Odd Function: Areas Cancel" );
|
![[Maple Plot]](images/EvaluateDefInt85.gif)
In the above graph notice how the positive pink area exactly cancels the negative cyan area.
This suggests that
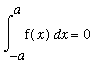 .
.
To prove this fact for any (integrable) odd function, separate the original interval [
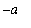 ,
,
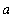 ] into two region [
] into two region [
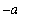 , 0 ] and [ 0,
, 0 ] and [ 0,
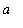 ]. For the integral on [
]. For the integral on [
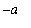 , 0 ] use the substitution
, 0 ] use the substitution
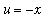 . Then
. Then
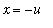 and
and
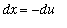 and the resulting integral is:
and the resulting integral is:
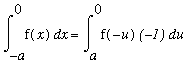 ( Substitution )
( Substitution )
=
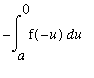 ( Algebra )
( Algebra )
=
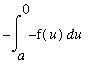 ( Definition of Odd Function )
( Definition of Odd Function )
=
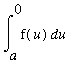 ( Algebra )
( Algebra )
=
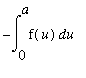 ( Property of Definite Integral )
( Property of Definite Integral )
Then, recalling that the integration variable in a definite integral does not make a difference to the value of the integral
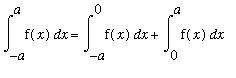
=
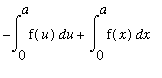
= 0.
One example of how this fact could be used to evaluate a definite integral of an odd function over a non-symmetric interval is as follows:: To evaluate
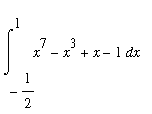 one could use the fact that the integrand is an odd function to reduce the problem over a shorter interval:
one could use the fact that the integrand is an odd function to reduce the problem over a shorter interval:
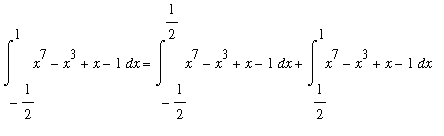
=
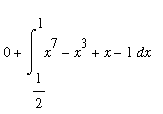
This computation is somewhat simpler in that it does not require handling all the negative signs that could arise from a lower limit of
 .
.
Example 4: Even Function on a Symmetric Interval
Recall that an even function is a function with the property that
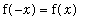 . An even function is said to be symmetric about the
. An even function is said to be symmetric about the
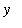 -axis. When an even function is integrated over a symmetric interval [
-axis. When an even function is integrated over a symmetric interval [
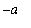 ,
,
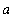 ] (
] (
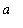 > 0 ) the value of the integral can be simplified. Suppose that
> 0 ) the value of the integral can be simplified. Suppose that
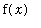 > 0 for
> 0 for
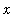 > 0. Then, by symmetry, the "area" under the curve on the interval [
> 0. Then, by symmetry, the "area" under the curve on the interval [
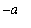 , 0 ] is the same as the area under the curve on the interval [ 0,
, 0 ] is the same as the area under the curve on the interval [ 0,
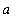 ].
].
| > |
P3 := plot( abs(x+sin(3*x)), x=-Pi..0, filled=true, color=cyan ):
display( P3,P2, title="Even Function: Areas Match" );
|
![[Maple Plot]](images/EvaluateDefInt115.gif)
In the above graph notice how the positive pink area exactly matches the negative cyan area.
This suggests that
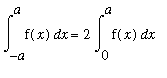 .
.
To prove this fact for any (integrable) even function, separate the original interval [
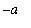 ,
,
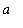 ] into two region [
] into two region [
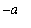 , 0 ] and [ 0,
, 0 ] and [ 0,
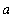 ]. For the integral on [
]. For the integral on [
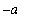 , 0 ] use the substitution
, 0 ] use the substitution
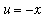 . Then
. Then
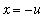 and
and
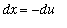 and the resulting integral is:
and the resulting integral is:
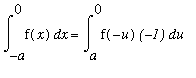 ( Substitution )
( Substitution )
=
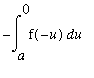 ( Algebra )
( Algebra )
=
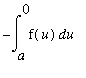 ( Definition of Even Function )
( Definition of Even Function )
=
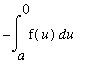 ( Algebra )
( Algebra )
=
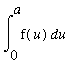 ( Property of Definite Integral )
( Property of Definite Integral )
Then, recalling that the integration variable in a definite integral does not make a difference to the value of the integral
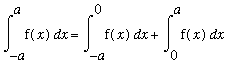
=
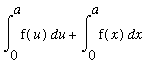
=
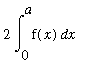
Example 5: Antiderivative for
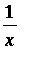
Recall that there is one power for which we do not know an antiderivative:
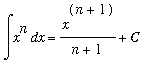 , for all
, for all
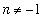 .
.
Now, because
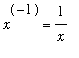 is continuous for all
is continuous for all
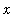 > 0, we know this function is Riemann integrable on ( 0,
> 0, we know this function is Riemann integrable on ( 0,
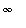 ). The First Fundamental Theorem of Calculus ensures that the antiderivative exists and can be written in terms of a definite integral:
). The First Fundamental Theorem of Calculus ensures that the antiderivative exists and can be written in terms of a definite integral:
| > |
f5 := 1/t:
F5 := Int( f5, t=1..x ):
L(x) = F5;
|
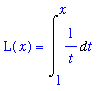
Let's discover a few properties of this antiderivative.
Property 1:
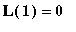
The properties for
Definite Integrals immediately tell us one function value for this function:
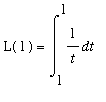 = 0.
= 0.
Property 2:
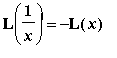
This property requires the use of the Method of Substitution with u=1/t. Then t=1/u, dt = -u^(-2)*du, and the limits of integration are converted from t=1 to u=1 and t=1/x to u=x. Thus
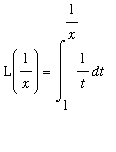
=
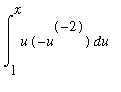
=
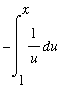
=
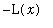 .
.
Property 3:
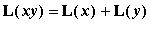
Let
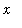 and
and
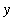 be positive numbers. Then, with a conveniently selected splitting of the interval [ 1,
be positive numbers. Then, with a conveniently selected splitting of the interval [ 1,
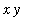 ] into [ 1,
] into [ 1,
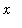 ]
]
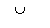 [
[
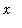 ,
,
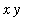 ].
].
:
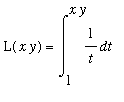
=
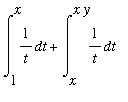
=
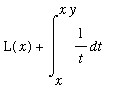
The remaining unidentified definite integral can be simplified with the substitution
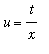 . Then
. Then
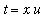 ,
,
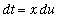 and the limits of integration are converted from
and the limits of integration are converted from
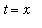 to
to
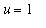 and
and
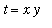 to
to
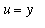 . When all of these facts are collected we find
. When all of these facts are collected we find
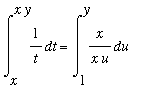
=
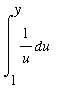
=
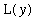 .
.
Thus, for all positive values of
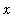 and
and
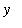 :
:
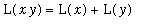 .
.
Property 4:
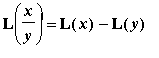
Properties 3 and 2 combine to yield this result:
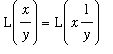 =
=
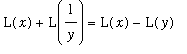 .
.
These properties are reminiscent of the properties of the (natural) logarithm function. To further justify this association, observe that the function L is increasing for all
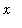 > 0 because
> 0 because
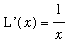 > 0. In particular, L(x) > 0 for all
> 0. In particular, L(x) > 0 for all
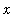 > 1 and
> 1 and
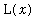 < 0 for all 0 <
< 0 for all 0 <
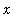 < 1. While L has no critical points, the fact that `L''`(x) = -1/x^2 < 0, the graph is always concave down. All of these features are present in the following graph of L
< 1. While L has no critical points, the fact that `L''`(x) = -1/x^2 < 0, the graph is always concave down. All of these features are present in the following graph of L
| > |
plot( F5, x=0..10, title="L(x) = ln(x)" );
|
![[Maple Plot]](images/EvaluateDefInt179.gif)
All of the properties and the above graph lead us to conclude that
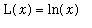 , the natural logarithm.
, the natural logarithm.
Lesson Summary
The Method of Substitution is the one integration technique considered in this course. This method provides an antiderivative version of the
Power Rule for differentiation. This method greatly expands the integrals that can be compute explicitly. Additional methods, particularly a antiderivative analog of the Product Rule, will be developed in the next course in the calculus sequence.
While the natural logarithm is not generally discussed in this course, the Method of Substitution and ideas from the
Graphing lesson strongly suggest that the natural logarithm is an antiderivative for
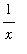 :
:
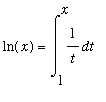 .
.
What's Next?
Now that you have completed this lesson, you should hone your integration (and antidifferentiation) skills with the
online homework assignment. The Integration maplet [
Maplet Viewer][
Maplenet] can be very helpful when exploring how different substitutions change an integral. There are practice sessions for specific types of integrals, a general practice session for problems related to this lesson, and a graded homework assignment. Work enough practice problems to master these concepts, then complete the online homework assignment and the
assigned problems from the text.
The
Definite Integrals,
Fundamental Theorems of Calculus, and
Evaluating Definite Integrals lessons are the source of questions for
Quiz 8.
The last unit in this course presents a collection of
Applications of the Integral. The applications begin with the theoretical
Mean Value Theorem for Integrals, then consider three topics from geometry ---
Area of a Plane Region,
Volume of a Solid,
Length of a Plane Curve, before concluding with one application from physics ---
Work.
![]() and properties of this antiderivative are discussed in detail.
and properties of this antiderivative are discussed in detail.
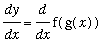 =
=
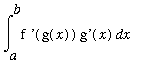 =
=
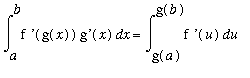 =
=
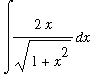 .
.
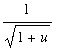 is not immediately known. But,
is not immediately known. But,
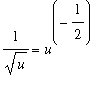 is known
is known
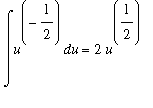 .
.
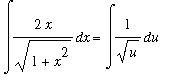
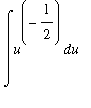
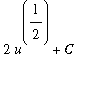
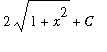 .
.
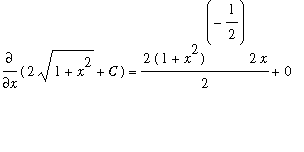
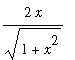 .
.
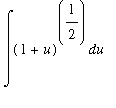 . As this is not a form for any of our known antiderivatives, this is a deadend for us.
. As this is not a form for any of our known antiderivatives, this is a deadend for us.
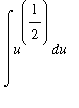 --- success! Click the
Power
button to have the
--- success! Click the
Power
button to have the
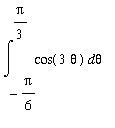 .
.
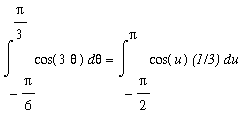
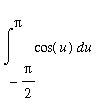
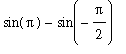 )
)
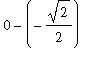 )
)
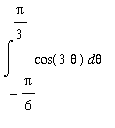 =
=
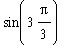 -
-
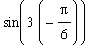 )
)
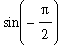
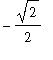 )
)
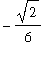
![[Maple Plot]](images/EvaluateDefInt85.gif)
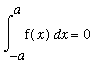 .
.
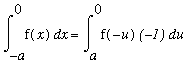 ( Substitution )
( Substitution )
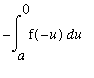 ( Algebra )
( Algebra )
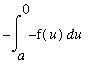 ( Definition of Odd Function )
( Definition of Odd Function )
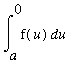 ( Algebra )
( Algebra )
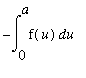 ( Property of Definite Integral )
( Property of Definite Integral )
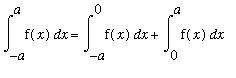
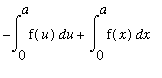
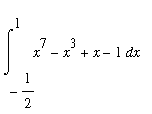 one could use the fact that the integrand is an odd function to reduce the problem over a shorter interval:
one could use the fact that the integrand is an odd function to reduce the problem over a shorter interval:
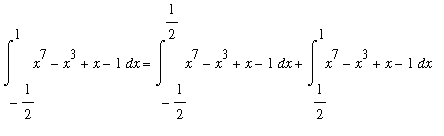
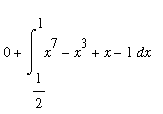
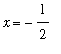 .
.
![[Maple Plot]](images/EvaluateDefInt115.gif)
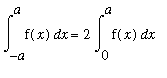 .
.
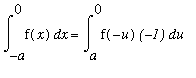 ( Substitution )
( Substitution )
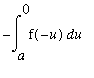 ( Algebra )
( Algebra )
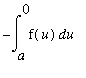 ( Definition of Even Function )
( Definition of Even Function )
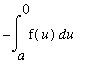 ( Algebra )
( Algebra )
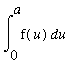 ( Property of Definite Integral )
( Property of Definite Integral )
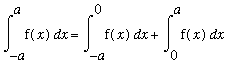
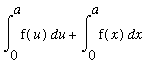
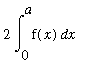
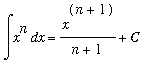 , for all
, for all
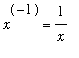 is continuous for all
is continuous for all
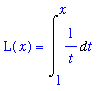
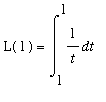 = 0.
= 0.
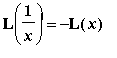
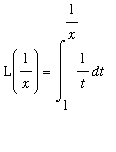
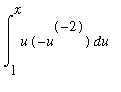
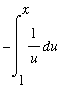
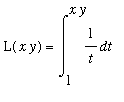
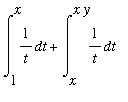
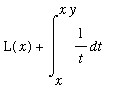
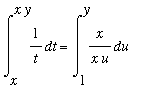
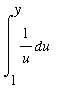
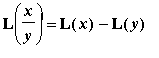
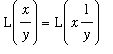 =
=
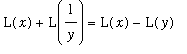 .
.
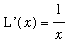 > 0. In particular, L(x) > 0 for all
> 0. In particular, L(x) > 0 for all
![[Maple Plot]](images/EvaluateDefInt179.gif)
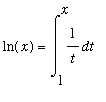 .
.