Lesson Overview
Limits of expressions involving the trigonometric functions can be evaluated by direct substitution --- unless division by zero is encountered. When division by zero is encountered, simplifications such as the ones presented in the Conceptual Understanding of Limits lesson can be attempted. In many cases, however, this is not enough to evaluate a limit. The two special limits
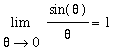 and
and
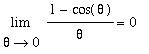 .
.
were introduced -- graphically -- in the Conceptual Understanding of Limits lesson. In the current lesson each of these limits will be rigorously evaluated. These proofs will be our first real application of the Limit Laws, particularly the Squeeze Theorem.
| > |
![[Maple Plot]](images/LimitTrig4.gif)
![MATRIX([[Limit, Restrictions], [__________________, _____________], [limit(sin(theta),theta = c) = sin(c), none], [limit(cos(theta),theta = c) = cos(c), none]])](images/LimitTrig5.gif)
![MATRIX([[Limit, Restrictions], [__________________, _____________], [limit(tan(theta),theta = c) = tan(c), c <> (2*n+1)*Pi/2], [limit(cot(theta),theta = c) = cot(c), c <> n*Pi], [limit(sec(theta),theta...](images/LimitTrig6.gif)
![[Maple Plot]](images/LimitTrig9.gif)
![[Maple Plot]](images/LimitTrig10.gif)
![[Maple Plot]](images/LimitTrig11.gif)
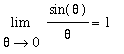 and
and
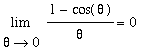 .
.
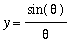 and
and
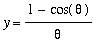 are suggestive, they are not proofs.
are suggestive, they are not proofs.
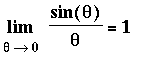
![[Maple Plot]](images/LimitTrig17.gif)
![[Maple Plot]](images/LimitTrig18.gif)
![[Maple Plot]](images/LimitTrig20.gif)
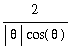 and obtain:
and obtain:
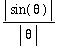 <=
<=
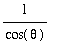
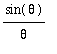 > 0 and so
> 0 and so
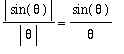 . This means
. This means
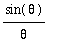 <=
<=
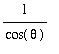
![[Maple Plot]](images/LimitTrig51.gif)
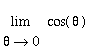 =
=
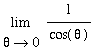 = 1, the Squeeze Theorem is applicable and tells us that
= 1, the Squeeze Theorem is applicable and tells us that
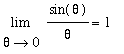 .
.
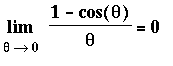
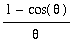 by
by
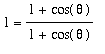 and then using trigonometric identities to simplify:
and then using trigonometric identities to simplify:
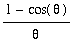 =
=
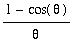
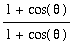
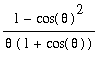
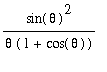
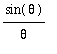
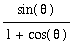
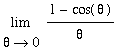 =
=
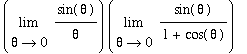 = (1)(0) = 0
= (1)(0) = 0
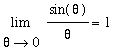 and
and
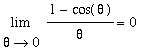 .
.