Continuity at a Point
Definition - Continuity at a Point
A function f is
continuous at a point
![]() if the following three conditions are satisfied:
if the following three conditions are satisfied:
i)
![]() is in the domain of f, i.e.,
is in the domain of f, i.e.,
![]() exists
exists
ii)
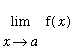 exists
exists
iii)
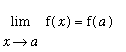
If any one of these three conditions is not satisfied, the function is said to be
discontinuous at
![]() .
.
| > |
When a function, f, is undefined at an isolated point,
![]() , then
, then
![]() is called a
singularity
of the function. If it is possible to define
is called a
singularity
of the function. If it is possible to define
![]() so that the modified function is continous at
so that the modified function is continous at
![]() then
then
![]() is called a
removable singularity of
f; if not, then
is called a
removable singularity of
f; if not, then
![]() is called an
essential singularity
of f.
is called an
essential singularity
of f.
| > |
Example 1 - Removable Singularity
Consider the function
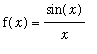 . Because this function is not defined at
. Because this function is not defined at
![]() it is discontinuous at 0.
it is discontinuous at 0.
But, because
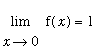 , if
, if
![]() , then the resulting function, namely,
, then the resulting function, namely,
![f(x) = PIECEWISE([sin(x)/x, x <> 0],[1, x = 0])](images/LimitContinuity17.gif)
is continuous at
![]() .
.
A plot of the modified function clearly shows how this definition of
![]() agrees with the limit at 0.
agrees with the limit at 0.
| > | f := x -> piecewise( x=0, 1, sin(x)/x ): p1 := plot( f, -3*Pi..-0.1 ): p2 := plot( f, 0.1..3*Pi ): p3 := pointplot( [0,f(0)], style=point, symbol=circle, symbolsize=18, color=red ): display( [p1,p2,p3], title="Plot showing continuity of modified function at x=0" ); |
![[Maple Plot]](images/LimitContinuity20.gif)
Observe that if the red circle were located anywhere else along the vertical axis the function would be discontinuous at
![]() .
.
| > |
Example 2 - Essential Singularity
The function
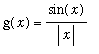 is related to the function f in Example 1:
is related to the function f in Example 1:
![]() for
for
![]() > 0 and
> 0 and
![]() for
for
![]() < 0. Because g(0) is not defined, g is discontinuous at
< 0. Because g(0) is not defined, g is discontinuous at
![]() because of the singularity at 0.
because of the singularity at 0.
However, unlike Example 1, it is not possible to define
![]() to remove the singularity. Another way to show that g is discontinuous at
to remove the singularity. Another way to show that g is discontinuous at
![]() is:
is:
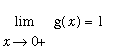 and
and
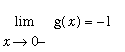 means that
means that
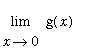 does not exist.
does not exist.
The different values for the one-sided limits means it is not possible to define
![]() to remove the singularity at 0.
to remove the singularity at 0.
The nature of the essential singularity of this function at 0 is easily seen in the following plot.
| > | g := x -> piecewise( x=0, undefined, sin(x)/abs(x) ): p4 := plot( g, -3*Pi..-0.1 ): p5 := plot( g, 0.1..3*Pi ): display( [p4,p5], title="Plot showing essential singularity of sin(x)/abs(x) at x=0" ); |
![[Maple Plot]](images/LimitContinuity34.gif)
| > |
If
![]() is an endpoint of the domain of the function, the limits in conditions ii) and iii) are replaced with the appropriate one-sided limits.
is an endpoint of the domain of the function, the limits in conditions ii) and iii) are replaced with the appropriate one-sided limits.
Example 3 - Continuity at Endpoints
Consider the function
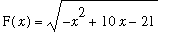 . The domain of this function is the set of all numbers
. The domain of this function is the set of all numbers
![]() such that
such that
![]() >= 0, that is 3 <=
>= 0, that is 3 <=
![]() <= 7.
<= 7.
| > | F := x -> sqrt( -x^2+10*x-21 ): p6 := plot( F, 3.0001..6.9999 ): p7 := pointplot( [[3,F(3)],[7,F(7)]], symbol=circle, symbolsize=18, color=red ): display( [p6,p7], view=[2..8,-0.1..2], title="Plot showing continuity at the endpoints of a domain" ); |
![[Maple Plot]](images/LimitContinuity40.gif)
The two-sided limits
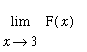 and
and
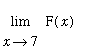 do not exist. However, because
do not exist. However, because
![]() is an endpoint of the domain of F,
is an endpoint of the domain of F,
![]() and
and
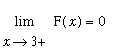 are enough to conclude that F is (right) continuous at
are enough to conclude that F is (right) continuous at
![]() . Similarly, F is (left) continuous at
. Similarly, F is (left) continuous at
![]() because
because
![]() and
and
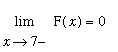 .
.
| > |
Example 4 - Continuity at Endpoints II
The function
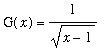 has domain ( 1,
has domain ( 1,
![]() ). Because this domain is open there are no endpoints to consider. Thus, because condition i) is not satisfied, G is not continuous at
). Because this domain is open there are no endpoints to consider. Thus, because condition i) is not satisfied, G is not continuous at
![]() . Moreover, because
. Moreover, because
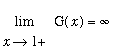 , there is no possibility to extend the domain to [ 1,
, there is no possibility to extend the domain to [ 1,
![]() ) to make G continuous at
) to make G continuous at
![]() .
.
This example, and the following plot, illustrate that a function cannot be continuous at a point where the function has a vertical asymptote.
| > | G := 1/sqrt(x-1): p8 := plot( G, x=1.01..50 ): p9 := implicitplot( x=1, x=0..50, y=0..10, color=cyan ): display( [p8,p9], view=[0..50,0..10], title="Plot of function and vertical asymptote; not continuous at x=1" ); |
![[Maple Plot]](images/LimitContinuity56.gif)
| > |
It is tempting to remember only condition iii). That is fine, provided you remember that if either the limit or the function value does not exist then the function is discontinuous at that point.
![MATRIX([
[Name, Formula, `Interval of Continuity`], [___________________, _______________
________, ____________________________], [Constant, F(x) = c, `all real numbers`
= (-infinity, infinity)], [Ident...](images/LimitContinuity65.gif)
 .
.
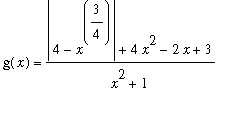 .
.
![[Maple Plot]](images/LimitContinuity71.gif)
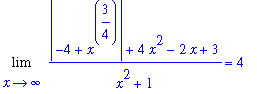
 and g attains this value only once, near
and g attains this value only once, near
![[Maple Plot]](images/LimitContinuity87.gif)
![[Maple Plot]](images/LimitContinuity88.gif)
![f(x) = PIECEWISE([x-1, x < 1],[5, 1 <= x])](images/LimitContinuity89.gif)
![g(x) = PIECEWISE([2*x, x < 1],[2-5*x, 1 <= x])](images/LimitContinuity90.gif)
![f(x)+g(x) = PIECEWISE([3*x-1, x < 1],[7-5*x, 1 <= x])](images/LimitContinuity92.gif) ,
,
![[Maple Plot]](images/LimitContinuity93.gif)