Lesson Overview
A limit at infinity is a limit in which the independent variable increases without bound. When we write
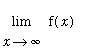 it is tempting to say that the limit point is infinity. But, infinity is not a real number and the limit requires special treatment in terms of the precise definition. We will not, however, devote any time to this epsilon-delta definition of limits at infinity. Instead we will concentrate on developing the intuitive understanding of limits at infinity and manipulative skills needed to evaluate these limits.
it is tempting to say that the limit point is infinity. But, infinity is not a real number and the limit requires special treatment in terms of the precise definition. We will not, however, devote any time to this epsilon-delta definition of limits at infinity. Instead we will concentrate on developing the intuitive understanding of limits at infinity and manipulative skills needed to evaluate these limits.
In this lesson we will learn a few techniques for evaluating limits at infinity without the use of a graph. In spite of the previous comments about the difficulties visualizing a limit at infinity, we will see how graphs can be used to assist with the evaluation of a limit at infinity. The Infinite Limits lesson continues some of the topics introduced here.
Reciprocal Powers and Rational Functions
The fundamental fact used to evaluate all limits at infinity for a rational function is the rather obvious statement
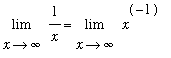 = 0.
= 0.
The Product, Power and Root Laws can be used to derive the limit at infinity for any (negative) power
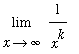 =
=
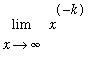 =
=
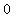 for all
for all
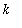 >0
>0
If
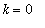 , then
, then
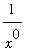 =
=
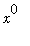 = 1 for all
= 1 for all
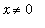 and so
and so
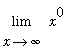 =
=
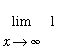 = 1
= 1
The limits at infinity for positive powers of x will be discussed in the
Infinite Limits lesson.
Graphical verification of these results is not really necessary. But, it is important that you thoroughly understand that
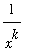 decreases towards zero more rapidly than
decreases towards zero more rapidly than
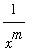 when
when
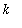 >
>
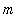 >0. This point is emphasized with the following plot.
>0. This point is emphasized with the following plot.
| > |
K := [ 0, 1/2, 1, 2, 3, 4]:
ff := [seq( 1/x^k, k=K )]:
ll := [seq( sprintf("k=%a",k), k=K )]:
plot( ff, x=0..10, y=0..1.2,
title="Plots of y=1/x^k for large positive values of x",
legend=ll,
color=[red,green,pink,cyan,blue,magenta] );
|
![[Maple Plot]](images/LimitAtInfinity17.gif)
The limit at infinity of a rational function in
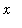 is typically evaluated by identifying the largest power of
is typically evaluated by identifying the largest power of
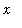 in the denominator and dividing both numerator and denominator by this power of
in the denominator and dividing both numerator and denominator by this power of
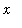 . The expression obtained from this manipulation will have a denominator whose limit at infinity exists and is not zero. If the numerator contains no positive powers of
. The expression obtained from this manipulation will have a denominator whose limit at infinity exists and is not zero. If the numerator contains no positive powers of
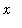 , then the Quotient Rule can be used to determine the value of this limit at infinity. The case with positive powers of
, then the Quotient Rule can be used to determine the value of this limit at infinity. The case with positive powers of
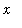 in the numerator will be discussed in the
Infinite Limits lesson.
in the numerator will be discussed in the
Infinite Limits lesson.
Example 1
For our first example, let's consider the limit at infinity of a rational function in which the numerator and denominator are both quintic polynomials
| > |
f1 := (63*x^5-39*x^4-48*x^3-94*x^2+10*x-20)/(70*x^5+98*x^4+58*x^3+45*x^2-12*x+28):
n1 := numer( f1 ):
d1 := denom( f1 ):
L1 := Limit( f1, x=infinity ):
L1;
|
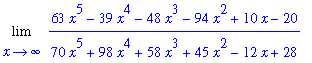
The leading degree in the denominator is
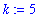
Dividing both numerator and denominator by
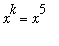 produces the equivalent problem
produces the equivalent problem
| > |
n2 := expand( n1/x^k ):
d2 := expand( d1/x^k ):
f2 := n2/d2:
L2 := Limit( f2, x=infinity ):
L1 = L2;
|
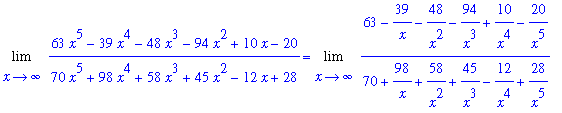
Note that the limit of the denominator exists and is non-zero:
| > |
d3 := Limit( d2, x=infinity ):
d3 = value(d3);
|
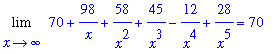
The Quotient Rule for limits can be applied to determine the value for this limit
| > |
L3 := Limit( n2, x=infinity ) / d3:
L2 = L3;
`` = value( L3 );
|
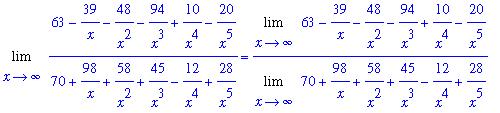
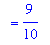
A plot of this function confirms that this result is reasonable.
| > |
plot( f1, x=1..200, discont=true );
|
![[Maple Plot]](images/LimitAtInfinity30.gif)
Note, however, that the graph is insufficient without the algebraic manipulation. It is possible that the function appears to settle down on a finite interval but has different behavior for even larger values of
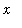 .
.
Example 2
Consider the limit at infinity of a rational function in which the denominator has a higher degree than the numerator:
| > |
f1 := (93*x^6+45*x^5+81*x^4+8*x^2-44*x-80)/(63*x^9-24*x^8-63*x^7-36*x^5+85*x^3+35):
n1 := numer( f1 ):
d1 := denom( f1 ):
L1 := Limit( f1, x=infinity ):
L1;
|
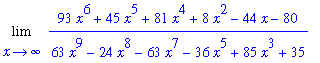
The leading degree in the denominator is
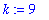
Dividing both numerator and denominator by
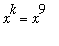 produces the equivalent problem
produces the equivalent problem
| > |
n2 := expand( n1/x^k ):
d2 := expand( d1/x^k ):
f2 := n2/d2:
L2 := Limit( f2, x=infinity ):
L1 = L2;
|
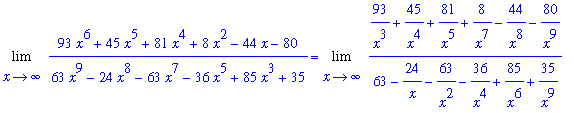
Note that the limit in the denominator exists and is non-zero:
| > |
d3 := Limit( d2, x=infinity ):
d3 = value(d3);
|
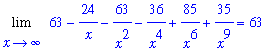
The Quotient Rule for limits can be applied to determine the value for this limit
| > |
L3 := Limit( n2, x=infinity ) / d3:
L2 = L3;
`` = value( L3 );
|
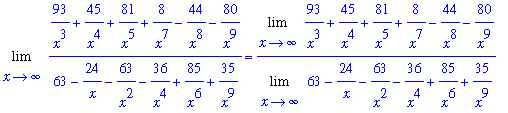
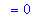
A plot of this function confirms that this result is reasonable.
| > |
plot( f1, x=1..10, discont=true );
|
![[Maple Plot]](images/LimitAtInfinity39.gif)
Note, however, that the graph is insufficient without the algebraic manipulation. It is possible that the function appears to settle down on a finite interval but has different behavior for even larger values of
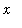 .
.
Limits at Negative Infinity
Limits at negative infinity can be converted to limits at infinity by a simple change for variables
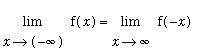 .
.
The limits
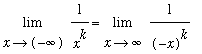 can be evaluated only when
can be evaluated only when
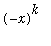 is defined. This means that
is defined. This means that
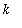 must be either an integer or a rational number with an odd denominator. The graph of
must be either an integer or a rational number with an odd denominator. The graph of
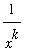 for negative values of
for negative values of
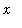 is closely related to the corresponding graph for positive values of
is closely related to the corresponding graph for positive values of
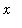 , but the exact relationship depends on whether
, but the exact relationship depends on whether
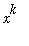 is an even or an odd function.
is an even or an odd function.
| > |
plot( ff, x=-10..0, y=-1.2..1.2,
title="Plots of y=1/x^k for large negative values of x",
legend=ll, color=[red,green,pink,cyan,blue,magenta] );
|
![[Maple Plot]](images/LimitAtInfinity69.gif)
Therefore, for
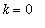
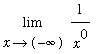 =
=
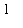
and for all positive rational values of
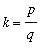 (in reduced form) with
(in reduced form) with
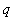 odd,
odd,
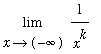 =
=
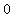 .
.
The fact limits at negative infinity are easily converted to limits at infinity means the techniques developed for limits at infinity can also be applied to limits at negative infinity.
Example 4
Note
Except that
infinity
is changed to
-infinity
, this discussion is exactly the same as the one in Example 1.
For our fourth example, let's consider the limit at negative infinity of a rational function in which the numerator and denominator are both quintic polynomials
| > |
f1 := (63*x^5-39*x^4-48*x^3-94*x^2+10*x-20)/(70*x^5+98*x^4+58*x^3+45*x^2-12*x+28):
n1 := numer( f1 ):
d1 := denom( f1 ):
L1 := Limit( f1, x=-infinity ):
L1;
|
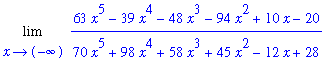
The leading degree in the denominator is
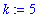
Dividing both numerator and denominator by
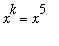 produces the equivalent problem
produces the equivalent problem
| > |
n2 := expand( n1/x^k ):
d2 := expand( d1/x^k ):
f2 := n2/d2:
L2 := Limit( f2, x=-infinity ):
L1 = L2;
|
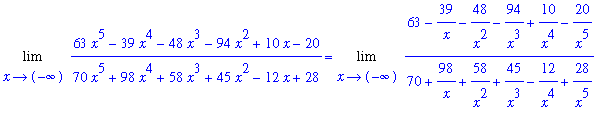
Note that the limit of the denominator exists and is non-zero:
| > |
d3 := Limit( d2, x=-infinity ):
d3 = value(d3);
|
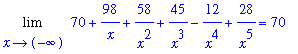
The Quotient Rule for limits can be applied to determine the value for this limit
| > |
L3 := Limit( n2, x=-infinity ) / d3:
L2 = L3;
`` = value( L3 );
|
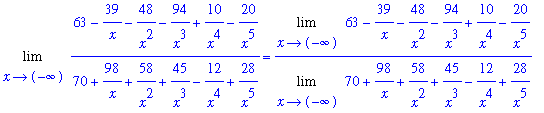
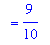
A plot of this function confirms that this result is reasonable.
| > |
plot( f1, x=-1000..-10, discont=true );
|
![[Maple Plot]](images/LimitAtInfinity84.gif)
Note, however, that the graph is insufficient without the algebraic manipulation. It is possible that the function appears to settle down on a finite interval but has different behavior for even larger values of
 .
.
Horizontal Asymptote
Definition - Horizontal Asymptote
A
horizontal asymptote
to the graph of
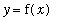 is a (horizontal) line
is a (horizontal) line
![y = y[h]](images/LimitAtInfinity87.gif) where
where
![limit(f(x),x = infinity) = y[h]](images/LimitAtInfinity88.gif) or
or
![limit(f(x),x = -infinity) = y[h]](images/LimitAtInfinity89.gif) .
.
Example 5
Find the horizontal asymptote(s) for
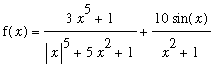 .
.
While the first term in this function is not a rational function, it can be handled exactly the same manner. Limits for the second term can be evaluated with the assistance of the Squeeze Theorem (as in Example 3).
| > |
f := (3*x^5+1)/(abs(x)^5+5*x^2+1) + 10*sin(x)/(x^2+1);
|
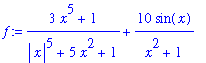
Observe that for
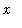 > 0,
> 0,
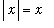 and so
and so
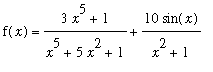 . The limit at infinity of this function is easily seen to be
. The limit at infinity of this function is easily seen to be
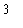 :
:
| > |
y_h1 := limit( f, x=infinity );
|
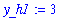
Similarly, for
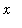 < 0,
< 0,
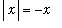 and so
and so
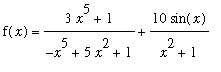 . The limit at negative infinity of this function is easily seen to be
. The limit at negative infinity of this function is easily seen to be
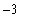 :
:
| > |
y_h2 := limit( f, x=-infinity );
|
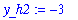
Graphical verification of these results can be seen in the following plot.
| > |
plot( [ f, y_h1, y_h2 ], x=-20..20, y=-5..5, discont=true,
color=[red,blue,green], legend=["y=f(x)", "y=3", "y=-3"] );
|
![[Maple Plot]](images/LimitAtInfinity102.gif)
Notice how the function oscillates but settles down to
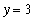 for large positive values of
for large positive values of
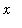 and to
and to
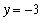 for large negative values of
for large negative values of
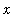 .
.
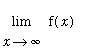 it is tempting to say that the limit point is infinity. But, infinity is not a real number and the limit requires special treatment in terms of the precise definition. We will not, however, devote any time to this epsilon-delta definition of limits at infinity. Instead we will concentrate on developing the intuitive understanding of limits at infinity and manipulative skills needed to evaluate these limits.
it is tempting to say that the limit point is infinity. But, infinity is not a real number and the limit requires special treatment in terms of the precise definition. We will not, however, devote any time to this epsilon-delta definition of limits at infinity. Instead we will concentrate on developing the intuitive understanding of limits at infinity and manipulative skills needed to evaluate these limits.
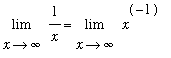 = 0.
= 0.
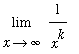 =
=
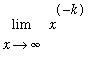 =
=
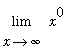 =
=
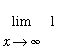 = 1
= 1
![[Maple Plot]](images/LimitAtInfinity17.gif)
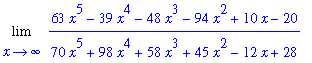
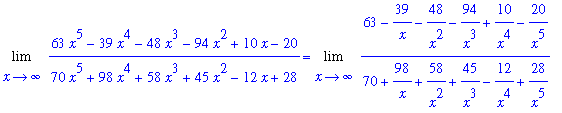
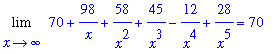
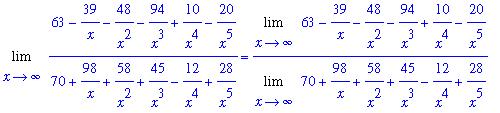
![[Maple Plot]](images/LimitAtInfinity30.gif)
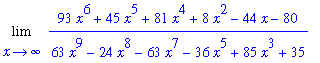
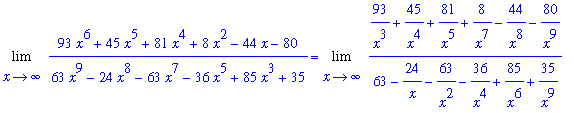
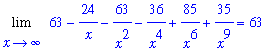
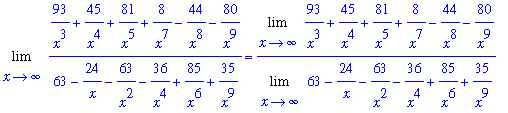
![[Maple Plot]](images/LimitAtInfinity39.gif)
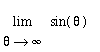 = d.n.e.
= d.n.e. 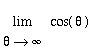 = d.n.e.
= d.n.e.
![[Maple Plot]](images/LimitAtInfinity47.gif)
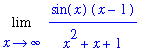
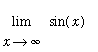 does not exist. In situations like this the Squeeze Theorem can be applied. The fact that the periodic function in this problem is bounded ( -1 <=
does not exist. In situations like this the Squeeze Theorem can be applied. The fact that the periodic function in this problem is bounded ( -1 <=
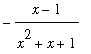 <=
<=
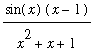 <=
<=
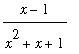 for all
for all
![[Maple Plot]](images/LimitAtInfinity57.gif)
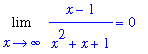
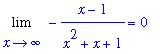
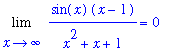
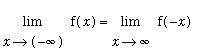 .
.
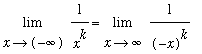 can be evaluated only when
can be evaluated only when
![[Maple Plot]](images/LimitAtInfinity69.gif)
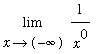 =
=
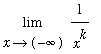 =
=
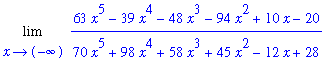
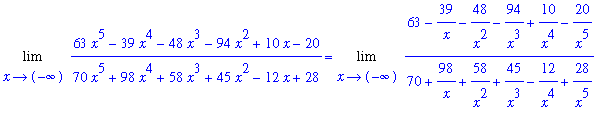
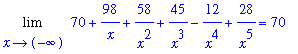
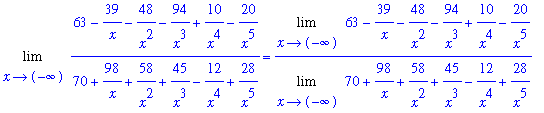
![[Maple Plot]](images/LimitAtInfinity84.gif)
![limit(f(x),x = infinity) = y[h]](images/LimitAtInfinity88.gif) or
or
![limit(f(x),x = -infinity) = y[h]](images/LimitAtInfinity89.gif) .
.
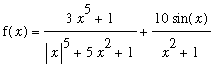 .
.
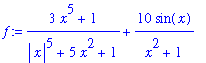
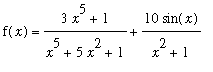 . The limit at infinity of this function is easily seen to be
. The limit at infinity of this function is easily seen to be
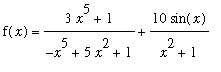 . The limit at negative infinity of this function is easily seen to be
. The limit at negative infinity of this function is easily seen to be
![[Maple Plot]](images/LimitAtInfinity102.gif)
![limit(1/(x^k),x = infinity) = PIECEWISE([0, `k > 0`],[1, k = 0])](images/LimitAtInfinity107.gif)