>

restart;

 

>	with( plots ):

 

>	with( LinearAlgebra ):

 

>	interface( rtablesize=20 ):

 

Warning, the name changecoords has been redefined 

>

 

Shrinking Circle Problem 

Numerical Evaluation of Analytic Formula for R 

in the Original Shrinking Circle Problem 

Douglas B. Meade 

9 February 2007 

>

 

>

 

>	rlist := [ 1, 0.5, 0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001, 0.00005, 0.00001 ]:

 

>	rlist2 := [ seq( 10.^(-j), j=0..15 ) ]:

 

>	dlist := [12,10,8,6,4]:

 

>

 

Here is Table 1. 

>	MakeTable( 1,0, rlist, dlist );

 

>

 

The effect of a vertical offset in the center of the fixed circle (b<>0) can be explored: 

>	MakeTable( 1, -1, rlist, dlist );

 

>	MakeTable( 1, -0.1, rlist, dlist );

 

>	MakeTable( 1, -0.01, rlist, dlist );

 

>

 

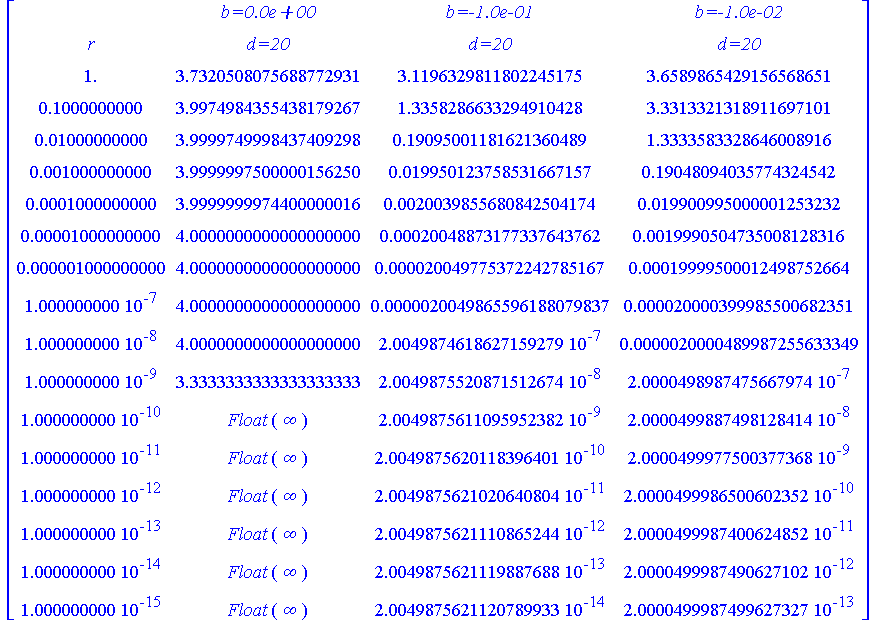
And, here is a single table of values allows us to see now even a very small vertical offset in the fixed circle changes the value of the limit 

>	blist := [0, seq( -10.^(-j), j=[1,2,4,6,8,10] ) ]:

 

>

<

 

>	Matrix( 1, 1+3, [ nprintf(""), seq( nprintf("b=%07.1e",b), b=blist[1..3] ) ] ),

 

>	Matrix( [ MakeTable( 1, blist[1], rlist2, [20] ), seq( Column( MakeTable( 1, b, rlist2, [20] ), 2 ), b=blist[2..3] ) ] )

 

>

>;

 

>

 

>

<

 

>	Matrix( 1, 1+1+2, [ nprintf(""), seq( nprintf("b=%07.1e",b), b=[blist[1],blist[4..5][]] ) ] ),

 

>	Matrix( [ MakeTable( 1, blist[1], rlist2, [20] ), seq( Column( MakeTable( 1, b, rlist2, [20] ), 2 ), b=blist[4..5] ) ] )

 

>

>;

 

>

 

>

<

 

>	Matrix( 1, 1+1+2, [ nprintf(""), seq( nprintf("b=%07.1e",b), b=[blist[1],blist[6..7][]] ) ] ),

 

>	Matrix( [ MakeTable( 1, blist[1], rlist2, [20] ), seq( Column( MakeTable( 1, b, rlist2, [20] ), 2 ), b=blist[6..7] ) ] )

 

>

>;

 

>