| > | restart; |
| > | with( plots ): |
| > | with( plottools ): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
| > |
Shrinking Circle Problem
Solution to the Original Shrinking Circle Problem
Douglas B. Meade
9 February 2007
| > |
| > | C := (x-1)^2+y^2=1^2; # fixed circle |
| > | Cr := r -> x^2+y^2=r^2; # shrinking circle |
| > | P := r -> [ 0, r ]; # top of shrinking circle |
![]()
![]()
![]()
| > |
| > | plotP := r -> plot( [P(r)], x=-1..1, style=point, symbol=circle, symbolsize=10, thickness=3, color=blue ): |
| > | plotC := implicitplot( C, x= 0..2, y=-1..1, color=pink ): |
| > | plotCr := r -> implicitplot( Cr(r), x=-r..r, y=-r..r, color=cyan ): |
| > | P1 := r -> display( [plotP(r),plotC,plotCr(r)], view=[-r..max(r,2),DEFAULT], scaling=constrained,
axes=normal, labels=["x","y"] ): |
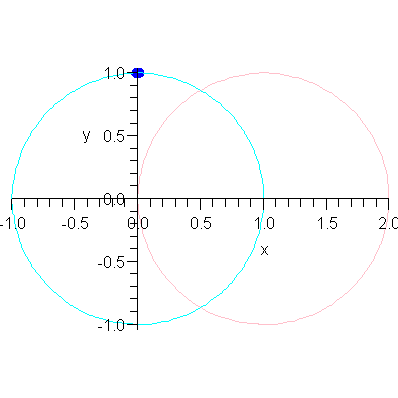
| > | P1(1,2); |
| > |
These circles intersect in two points.
| > | Intersection := [allvalues( solve( {C,Cr(r)}, {x,y} ) )] ; |
![(Typesetting:-mprintslash)([Intersection := [{x = 1/2*r^2, y = 1/2*(4-r^2)^(1/2)*r}, {x = 1/2*r^2, y = -1/2*(4-r^2)^(1/2)*r}]], [[{x = 1/2*r^2, y = 1/2*(4-r^2)^(1/2)*r}, {x = 1/2*r^2, y = -1/2*(4-r^2)...](images/OrigSC_5.gif)
![(Typesetting:-mprintslash)([Intersection := [{x = 1/2*r^2, y = 1/2*(4-r^2)^(1/2)*r}, {x = 1/2*r^2, y = -1/2*(4-r^2)^(1/2)*r}]], [[{x = 1/2*r^2, y = 1/2*(4-r^2)^(1/2)*r}, {x = 1/2*r^2, y = -1/2*(4-r^2)...](images/OrigSC_6.gif)
Of the two points, we want the one in the first quadrant
| > | X,Y := eval( [x,y], select( p->evalb( eval( y, eval(p,[r=1.]) )>0 ), Intersection )[] )[]:
x=X; y=Y; |
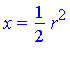
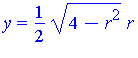
| > |
This is the formula for the point Q. .
| > |
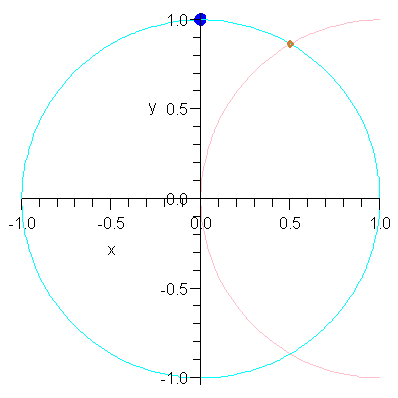
To construct the projection from the top of the shrinking circle through Q onto the y=0 plane,
| > | Q := unapply( [ X, Y ], [r,a] ): |
| > |
| > | plotQ := (r) -> plot( [Q(r)], color=gold, style=point, thickness=2 ): |
| > | P2 := (r) -> display( [plotP(r),plotC,plotCr(r),plotQ(r)],
axes=normal, labels=["x","y"], scaling=constrained ): |
| > | P2(1,2); |
| > |
For each angle theta, the lines passing through P and the point Q(theta) can be parameterized in terms of the (scaled) distance measured along this line.
| > | LinePQ := unapply( expand( (1-alpha)*P(r) + alpha*Q(r) ), [alpha,r] ); |
![(Typesetting:-mprintslash)([LinePQ := proc (alpha, r) options operator, arrow; [1/2*r^2*alpha, 1/2*(4-r^2)^(1/2)*r*alpha+r-r*alpha] end proc], [proc (alpha, r) options operator, arrow; [1/2*r^2*alpha,...](images/OrigSC_10.gif)
| > |
The value of the parameter alpha when these lines hit the z=0 plane are given by
| > | alpha0 := unapply( [simplify( solve( LinePQ(alpha,r)[2]=0, alpha ) ) assuming r>0][],
[r] ); |
![(Typesetting:-mprintslash)([alpha0 := proc (r) options operator, arrow; -2/((4-r^2)^(1/2)-2) end proc], [proc (r) options operator, arrow; -2/((4-r^2)^(1/2)-2) end proc])](images/OrigSC_11.gif)
| > |
Thus, the parametric representation of of the projected point, R, in the y=0 plane is
| > | R := unapply( [simplify( LinePQ(alpha0(r),r) ) assuming r>0][], [r] ); |
![(Typesetting:-mprintslash)([R := proc (r) options operator, arrow; [-r^2/((4-r^2)^(1/2)-2), 0] end proc], [proc (r) options operator, arrow; [-r^2/((4-r^2)^(1/2)-2), 0] end proc])](images/OrigSC_12.gif)
| > |
This completes the constructions needed to put all of this together in one animation.
| > | plotR := (r) -> plot( [P(r),R(r)], color=red, thickness=1 ): |
| > | P3 := (r,a) -> display( [P2(r),plotR(r)] ): |
| > |
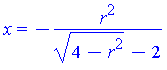
These plots already illustrate the rapid convergence of every point on the curves R - except the one on the x-axis - to the origin (as r->0). Let's look at the parametric form of R. The three components are:
| > | X,Y := R(r)[]:
x=X; y=Y; |
![]()
| > |
Maple does recognize the indeterminate form, and reports:
| > | limit( X, r=0, right ); |
![]()
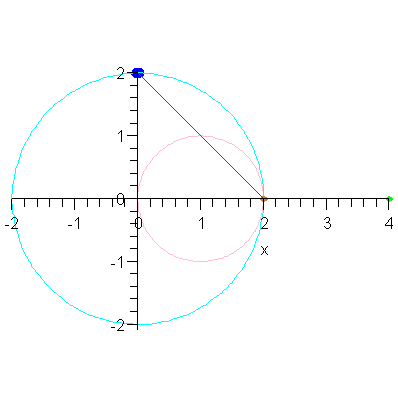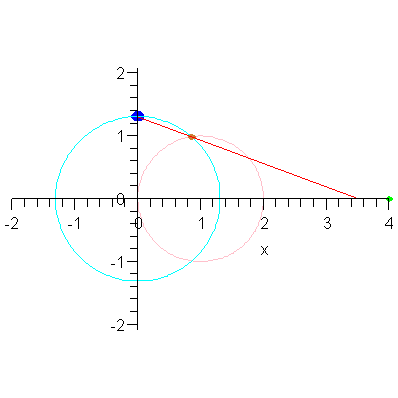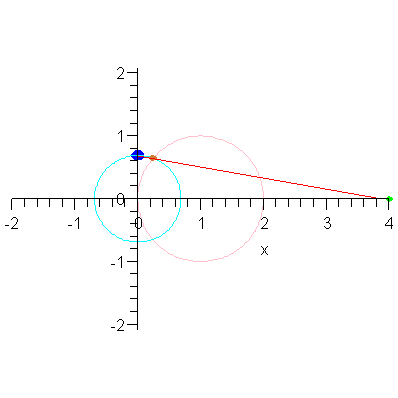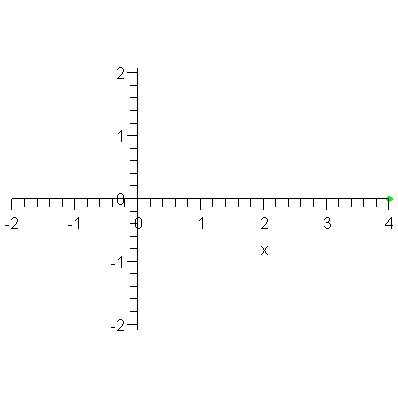
We close with a different animation that shows this convergence.
| > | plotR0 := plot( [[4,0]], x=0..4, color=green, style=point, thickness=2 ): |
| > | animR := animate( P3, [2-r], r=0..2, frames=30, numpoints=401, paraminfo=false, background=plotR0, view=[-2..max(2,4),DEFAULT] ): |
| > | animR; |
| > |