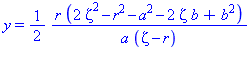LemmaSS-cone.mw
Shrinking Sphere Problem
Derivation of General Formula for Intersection of S and S_r,
and Its Projection from the Top of S_r onto the z=0 Plane
When S is a Cone
Douglas B. Meade
9 February 2007
Initial Configuration: the S (cone) and S_r (sphere) and the point P
| > |
S := (a,b) -> x^2+(y-a)^2=(z-b)^2; # fixed surface |
| > |
Sr := r -> x^2+y^2+z^2=r^2; # shrinking sphere |
| > |
P := r -> [ 0, 0, r ]; # top of shrinking sphere |
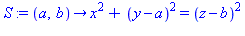
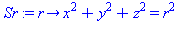
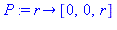
| > |
plotP := r -> plot3d( P(r), x=-1..1, y=-1..1, style=point, symbol=circle, symbolsize=10, color=blue ): |
| > |
plotS := (a,b) -> implicitplot3d( S(a,b), x= -2*b..2*b, y=a-2*b..a+2*b, z=-b..b,
color=pink, style=patchnogrid, transparency=0.8, grid=[25,25,25] ): |
| > |
plotSr := r -> implicitplot3d( Sr(r), x=-r..r, y=-r..r, z=-r..r,
color=cyan, style=patchnogrid, transparency=0.8 ): |
| > |
P1 := (r,a,b) -> display( [plotP(r),plotS(a,b),plotSr(r)],
axes=normal, labels=["x","y","z"], orientation=[25,65], args[4..-1] ): |
| > |
P1(1,1,1, scaling=constrained); |
Construction of Q: Intersection of S and S_r
The intersection between these two spheres is a circle, parallel to the x=0 plane.
| > |
Intersection := [allvalues( solve( {S(a,b),Sr(r)}, {x,y,z} ) )] ; |
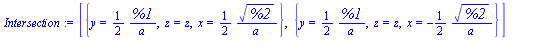
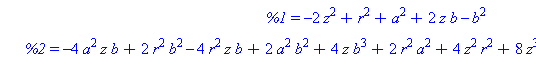
There are two parts to this solution.
| > |
xPOS := p->evalb( eval(x, eval(p,[r=1.,a=1.,b=1.,z=0.]))>0 ): |
| > |
Q := [ unapply( eval( [x,y,z], select( xPOS, Intersection )[] ), [z,r,a,b] ), |
| > |
unapply( eval( [x,y,z], remove( xPOS, Intersection )[] ), [z,r,a,b] ) ]: |
| > |
piecewise( x>0, Q[1](z,r,a,b), x<0, Q[2](z,r,a,b) ); |
![piecewise(0 < x, [1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)/a, 1/2*(-2*z^2+r^2+a^2+2*z*b-b^2)/a, z], x < 0, [-1/2*(-4*a^2*z*b...](images/LemmaSS-cone_6.gif)
![piecewise(0 < x, [1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)/a, 1/2*(-2*z^2+r^2+a^2+2*z*b-b^2)/a, z], x < 0, [-1/2*(-4*a^2*z*b...](images/LemmaSS-cone_7.gif)
To construct the projection from the top of the shrinking sphere through Q onto the z=0 plane, the parameterization of Q can be done in terms of z, ranging from the lowest value of 0 to the maximum value of
| > |
zM := (r,a,b) -> b*r/sqrt(a^2+b^2); |
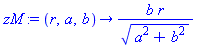
(and back down to zero). Actually, the intersection exists for all z from -zM to zM (with x>0) and back down to -zM (with x<0)
This curve is not easily identified.
| > |
plotQ := (r,a,b) -> display( [seq( |
| > |
spacecurve( Q[i](z,r,a,b), z=-zM(r,a,b)..zM(r,a,b), color=gold, thickness=2 ), |
| > |
P2 := (r,a,b) -> display( [plotP(r),plotS(a,b),plotSr(r),plotQ(r,a,b)],
axes=normal, labels=["x","y","z"], orientation=[45,60], scaling=constrained ): |
Construction of R: Projection of Q, from P, onto z=0 plane
For each angle theta, the lines passing through P and the point Q(theta) can be parameterized in terms of the (scaled) distance measured along this line.
| > |
LinePQ := [seq( unapply( expand( (1-alpha)*P(r) + alpha*Q[i](z,r,a,b) ), [alpha,z,r,a,b] ), i=1..2 )]: |
| > |
piecewise( x>0, LinePQ[1](alpha,z,r,a,b), x<0, LinePQ[2](alpha,z,r,a,b) ); |
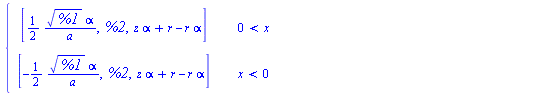
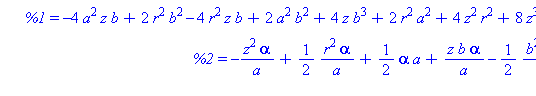
The value of the parameter alpha when these lines hit the z=0 plane are given by
| > |
alpha0 := unapply( [simplify( solve( LinePQ[1](alpha,z,r,a,b)[3]=0, alpha ) ) assuming a>0, r>0][],
[z,r,a,b] ); |
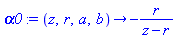
Thus, the parametric representation of of the projected curve, R, in the z=0 plane is
| > |
R := [seq( unapply( [simplify( LinePQ[i](alpha0(z,r,a,b),z,r,a,b) ) assuming a>0, b>0, r>0][], [z,r,a,b] ), i=1..2 )]: |
| > |
piecewise( x>0, R[1](z,r,a,b), x<0, R[2](z,r,a,b) ); |
![piecewise(0 < x, [-1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)*r/(a*(z-r)), 1/2*r*(2*z^2-r^2-a^2-2*z*b+b^2)/(a*(z-r)), 0], x < ...](images/LemmaSS-cone_12.gif)
![piecewise(0 < x, [-1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)*r/(a*(z-r)), 1/2*r*(2*z^2-r^2-a^2-2*z*b+b^2)/(a*(z-r)), 0], x < ...](images/LemmaSS-cone_13.gif)
This completes the constructions needed to put all of this together in one animation.
| > |
plotR := (r,a,b) -> display( [seq( spacecurve( R[i](z,r,a,b), z=-zM(r,a,b).. zM(r,a,b), numpoints=201, color=red, thickness=1 ), i=1..2 )] ): |
| > |
P3 := (r,a,b) -> display( [P2(r,a,b),plotR(r,a,b)] ): |
| > |
animQ := (r,a,b) -> display( [seq( animate( spacecurve, [LinePQ[i](alpha,z,r,a,b), alpha=0..alpha0(z,r,a,b)], z=-zM(r,a,b).. zM(r,a,b),
color=blue, thickness=2, orientation=[25,65], background=P3(r,a,b),
scaling=constrained, frames=21 ), i=1..2 )] ): |
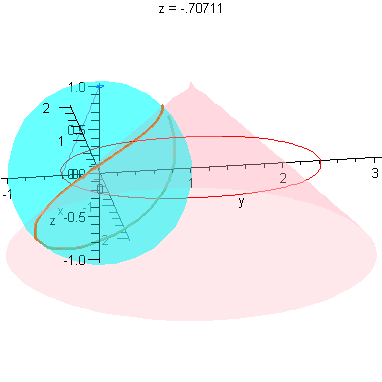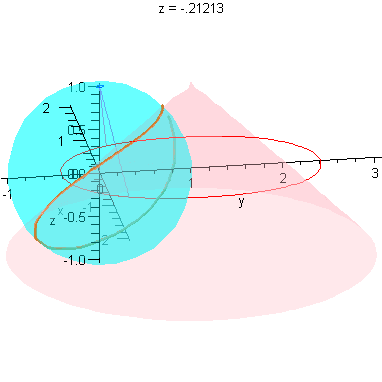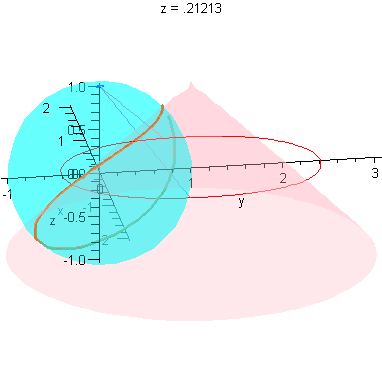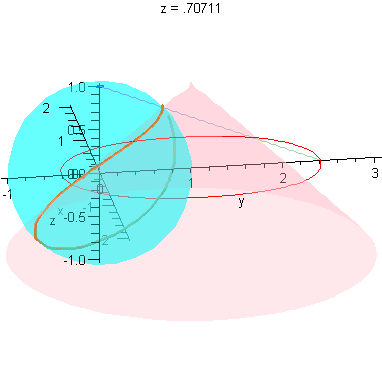
Limit as r -> 0
These plots already illustrate the rapid convergence of every point on the curves R - except the one on the x-axis - to the origin (as r->0). Let's look at the parametric form of R. The three components are (for x>0):
| > |
X,Y,Z := R[2](zeta,r,a,b)[]:
x=X;
y=Y;
z=Z; |
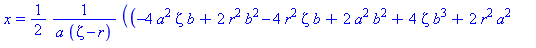
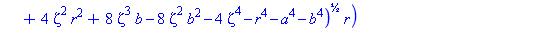
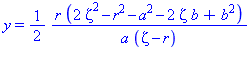
Notice that, since a<>0, the maximum value of the parameter is strictly less than r. Hence, there are no indeterminate forms, and each of the above expressions converges to 0 (as r->0).
| > |
map( limit, [X,Y,Z], r=0, right ); |
![[0, 0, 0]](images/LemmaSS-cone_19.gif)
We close with an animation that shows this convergence.
| > |
#to3d := transform( (x,y)->[x,y,0] ): |
| > |
#plotR0 := a -> to3d( implicitplot( x^2 + (y-2*a)^2 = 4*a^2, x=-2*a..2*a, y=0..4*a, color=green ) ): |
| > |
animR := (a,b) -> animate( P3, [1-r,a,b], r=0..1, frames=20, numpoints=201, paraminfo=false ):#, background=plotR0(a) ): |
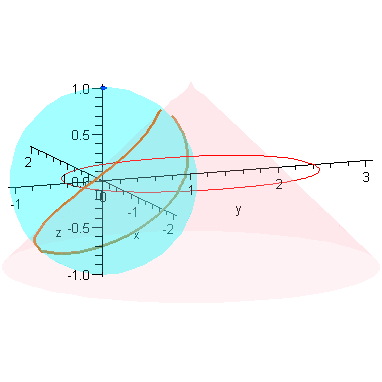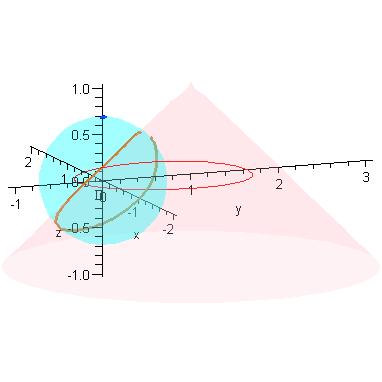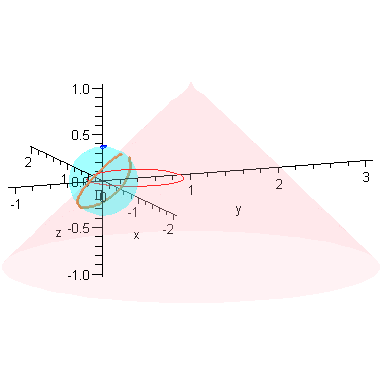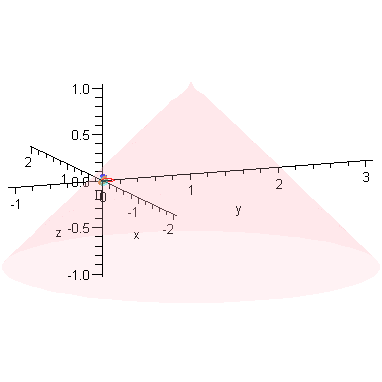
![]()
![]()
![]()
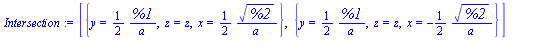
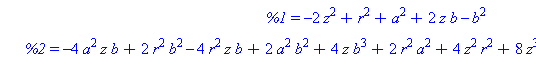
![piecewise(0 < x, [1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)/a, 1/2*(-2*z^2+r^2+a^2+2*z*b-b^2)/a, z], x < 0, [-1/2*(-4*a^2*z*b...](images/LemmaSS-cone_6.gif)
![piecewise(0 < x, [1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)/a, 1/2*(-2*z^2+r^2+a^2+2*z*b-b^2)/a, z], x < 0, [-1/2*(-4*a^2*z*b...](images/LemmaSS-cone_7.gif)
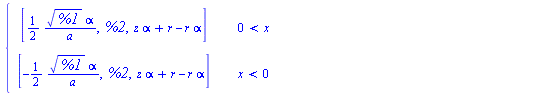
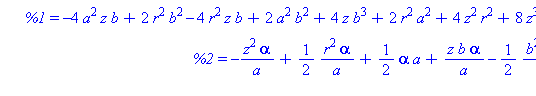
![piecewise(0 < x, [-1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)*r/(a*(z-r)), 1/2*r*(2*z^2-r^2-a^2-2*z*b+b^2)/(a*(z-r)), 0], x < ...](images/LemmaSS-cone_12.gif)
![piecewise(0 < x, [-1/2*(-4*a^2*z*b+2*r^2*b^2-4*r^2*z*b+2*a^2*b^2+4*z*b^3+2*r^2*a^2+4*z^2*r^2+8*z^3*b-8*z^2*b^2-4*z^4-r^4-a^4-b^4)^(1/2)*r/(a*(z-r)), 1/2*r*(2*z^2-r^2-a^2-2*z*b+b^2)/(a*(z-r)), 0], x < ...](images/LemmaSS-cone_13.gif)