LemmaSC.mw
Shrinking Circle Problem
Enhanced Solution to the Original Shrinking Circle Problem
Douglas B. Meade
9 February 2007
| > |
C := a -> (x-a)^2+y^2=a^2; # fixed circle |
| > |
Cr := r -> x^2+y^2=r^2; # shrinking circle |
| > |
P := r -> [ 0, r ]; # top of shrinking circle |
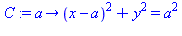
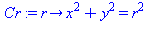
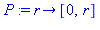
| > |
plotP := r -> plot( [P(r)], x=-1..1, style=point, symbol=circle, symbolsize=10, thickness=3, color=blue ): |
| > |
plotC := a -> implicitplot( C(a), x= 0..2*a, y=-a..a, color=pink ): |
| > |
plotCr := r -> implicitplot( Cr(r), x=-r..r, y=-r..r, color=cyan ): |
| > |
P1 := (r,a) -> display( [plotP(r),plotC(a),plotCr(r)], view=[-r..max(r,2*a),DEFAULT], scaling=constrained,
axes=normal, labels=["x","y"] ): |
These circles intersect in two points.
| > |
Intersection := [allvalues( solve( {C(a),Cr(r)}, {x,y} ) )] ; |
![[{x = 1/2*r^2/a, y = 1/2*(-r^2+4*a^2)^(1/2)*r/a}, {x = 1/2*r^2/a, y = -1/2*(-r^2+4*a^2)^(1/2)*r/a}]](images/LemmaSC_4.gif)
![[{x = 1/2*r^2/a, y = 1/2*(-r^2+4*a^2)^(1/2)*r/a}, {x = 1/2*r^2/a, y = -1/2*(-r^2+4*a^2)^(1/2)*r/a}]](images/LemmaSC_5.gif)
Of the two points, we want the one in the first quadrant
| > |
X,Y := eval( [x,y], select( p->evalb( eval( y, eval(p,[r=1.,a=1.]) )>0 ), Intersection )[] )[]:
x=X;
y=Y; |
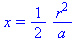
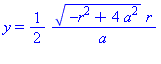
This is the formula for the point Q. .
To construct the projection from the top of the shrinking circle through Q onto the y=0 plane,
| > |
Q := unapply( [ X, Y ], [r,a] ): |
| > |
plotQ := (r,a) -> plot( [Q(r,a)], color=gold, style=point, thickness=2 ): |
| > |
P2 := (r,a) -> display( [plotP(r),plotC(a),plotCr(r),plotQ(r,a)],
axes=normal, labels=["x","y"], scaling=constrained ):
|
For each angle theta, the lines passing through P and the point Q(theta) can be parameterized in terms of the (scaled) distance measured along this line.
| > |
LinePQ := unapply( expand( (1-alpha)*P(r) + alpha*Q(r,a) ), [alpha,r,a] ); |
![proc (alpha, r, a) options operator, arrow; [1/2*r^2*alpha/a, 1/2*(-r^2+4*a^2)^(1/2)*r*alpha/a+r-r*alpha] end proc](images/LemmaSC_8.gif)
The value of the parameter alpha when these lines hit the z=0 plane are given by
| > |
alpha0 := unapply( [simplify( solve( LinePQ(alpha,r,a)[2]=0, alpha ) ) assuming a>0, r>0][],
[r,a] ); |
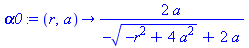
Thus, the parametric representation of of the projected point, R, in the y=0 plane is
| > |
R := unapply( [simplify( LinePQ(alpha0(r,a),r,a) ) assuming a>0, r>0][], [r,a] ); |
![proc (r, a) options operator, arrow; [r^2/(-(-r^2+4*a^2)^(1/2)+2*a), 0] end proc](images/LemmaSC_10.gif)
This completes the constructions needed to put all of this together in one animation.
| > |
plotR := (r,a) -> plot( [P(r),R(r,a)], color=red, thickness=1 ): |
| > |
P3 := (r,a) -> display( [P2(r,a),plotR(r,a)] ): |
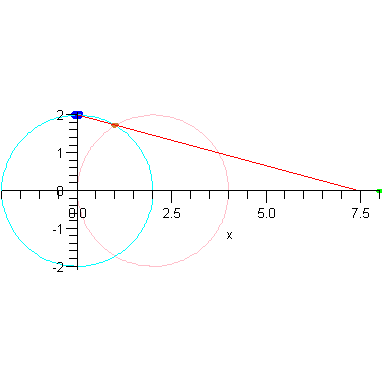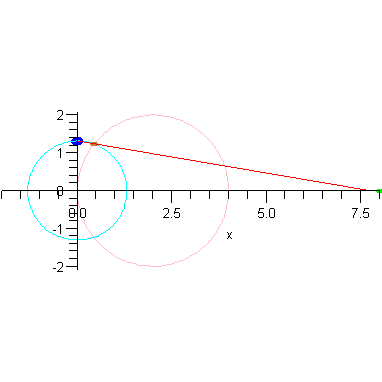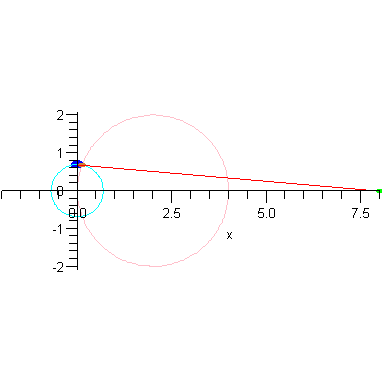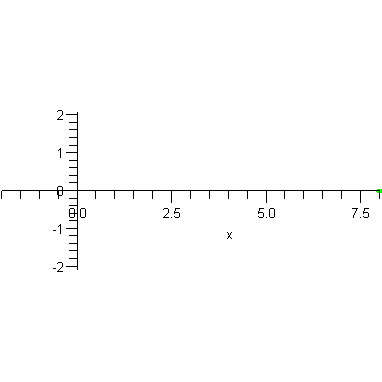
These plots already illustrate the rapid convergence of every point on the curves R - except the one on the x-axis - to the origin (as r->0). Let's look at the parametric form of R. The three components are:
| > |
X,Y := R(r,a)[]:
x=X;
y=Y; |
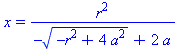
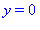
Maple does not recognize the indeterminate form, initially,
| > |
limit( X, r=0, right ); |
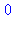
but once it is given some information about the parameter a, all is fine:
| > |
limit( X, r=0, right ) assuming a>0; |
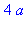
We close with a different animation that shows this convergence.
| > |
plotR0 := a -> plot( [[4*a,0]], x=0..4*a, color=green, style=point, thickness=2 ): |
| > |
animR := a -> animate( P3, [2-r,a], r=0..2, frames=30, numpoints=401, paraminfo=false, background=plotR0(a), view=[-2..max(2,4*a),DEFAULT] ): |
![]()
![]()
![]()
![[{x = 1/2*r^2/a, y = 1/2*(-r^2+4*a^2)^(1/2)*r/a}, {x = 1/2*r^2/a, y = -1/2*(-r^2+4*a^2)^(1/2)*r/a}]](images/LemmaSC_4.gif)
![[{x = 1/2*r^2/a, y = 1/2*(-r^2+4*a^2)^(1/2)*r/a}, {x = 1/2*r^2/a, y = -1/2*(-r^2+4*a^2)^(1/2)*r/a}]](images/LemmaSC_5.gif)
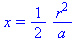
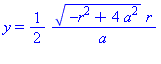
![proc (alpha, r, a) options operator, arrow; [1/2*r^2*alpha/a, 1/2*(-r^2+4*a^2)^(1/2)*r*alpha/a+r-r*alpha] end proc](images/LemmaSC_8.gif)
![]()
![proc (r, a) options operator, arrow; [r^2/(-(-r^2+4*a^2)^(1/2)+2*a), 0] end proc](images/LemmaSC_10.gif)
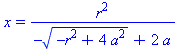
![]()
![]()
![]()
