Antiderivative.mws
Indefinite Integrals
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
All of our attention to date has been on the computation of derivatives. This unit turns things unpside down. Now, instead of finding the derivative a function you will be asked to identify a function based on information about its derivative. From the perspective of differentiation these functions are known as
antiderivatives
. (However, because the stem
anti
means
not
and the stem
retro
means
undo
, it seems that a more appropriate term would be retroderivative.) From the perspective of area (to be introduced later in the Riemann Sum and Definite Integral lessons of this unit) it makes more sense to talk about the
indefinite integral
of a function.
The goals of this lesson are
-
to become comfortable using the language of both antiderivatives and indefinite integrals,
-
to demonstrate that derivative formulae can be translated into antiderivative (or indefinite integral) formulae, and
-
to realize that the accuracy of any indefinite integral can be checked (by differentiation).
The graphical understanding of antiderivatives is greatly enhanced with the use of the
Antiderivative
maplet [
Maplet Viewer][
MapleNet].
Definition (Antiderivative/Indefinite Integral)
A function F is an
antiderivative
, or
indefinite integral
, of f on an interval
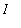 if
if
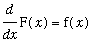 for all
for all
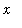 in
in
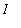 .
.
Notes
-
The definition provides a direct check to determine if F is, in fact, an antiderivative of f:
differentiate F (with respect to
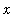 ) and compare this result with f on the interval
) and compare this result with f on the interval
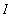
-
A common alternate notation for antiderivatives is to use
integral notation
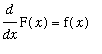 if and only if
if and only if
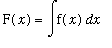 .
.
-
In the expression
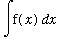 , read "the indefinite integral of
, read "the indefinite integral of
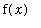 with respect to
with respect to
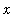 ", the first symbol (an elongated S) is called the
integral sign
, the
integrand
is
", the first symbol (an elongated S) is called the
integral sign
, the
integrand
is
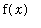 , and
, and
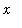 is the
variable of integration
. The integral sign and the dx should be viewed as a matched pair -- much like left- and right-parentheses.
is the
variable of integration
. The integral sign and the dx should be viewed as a matched pair -- much like left- and right-parentheses.
-
The definition and these notes are carefully written to state that F is an antiderivative of f (and not F is the antiderivative of f). The reason for this will be made very clear in the examples.
Example 1:
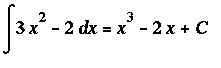
Let
| > |
f1 := 3*x^2 - 2:
f(x) = f1;
|
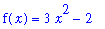
Consider the functions
| > |
F1 := x^3 - 2*x:
F[1](x) = F1;
|
 = x^3-2*x](images/Antiderivative16.gif)
| > |
F2 := x^3 - 3*x + 2:
F[2](x) = F2;
|
 = x^3-3*x+2](images/Antiderivative17.gif)
| > |
F3:= x^3 - 2*x + 3:
F[3](x) = F3;
|
 = x^3-2*x+3](images/Antiderivative18.gif)
Analytic Verification
From the derivatives of these functions:
| > |
dF1 := Diff( F1, x ):
dF1 = value( dF1 );
|
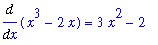
| > |
dF2 := Diff( F2, x ):
dF2 = value( dF2 );
|
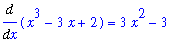
| > |
dF3 := Diff( F3, x ):
dF3 = value( dF3 );
|
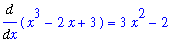
it is seen that F
![``[1]](images/Antiderivative22.gif) and F
and F
![``[3]](images/Antiderivative23.gif) are antiderivatives (indefinite integrals) of f and that F
are antiderivatives (indefinite integrals) of f and that F
![``[2]](images/Antiderivative24.gif) is
not
an antiderivative of f.
is
not
an antiderivative of f.
Graphical Verification
To understand why there can be more than one antiderivative of
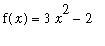 , consider the graph of F
, consider the graph of F
![``[1]](images/Antiderivative26.gif) , F
, F
![``[2]](images/Antiderivative27.gif) , and F
, and F
![``[3]](images/Antiderivative28.gif) on the interval [ -2, 2 ]:
on the interval [ -2, 2 ]:
| > |
plot( [ F1, F2, F3 ], x=-2..2,
color=[red,blue,green], legend=["y=F1", "y=F2", "y=F3" ] );
|
![[Maple Plot]](images/Antiderivative29.gif)
Observe that the graph of
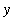 = F
= F
![``[3]](images/Antiderivative31.gif) is the graph of
is the graph of
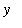 = F
= F
![``[1]](images/Antiderivative33.gif) shifted vertically by 3, i.e., F
shifted vertically by 3, i.e., F
![``[3]](images/Antiderivative34.gif) (
(
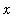 ) = F
) = F
![``[1]](images/Antiderivative36.gif) (
(
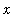 ) + 3. The graph of
) + 3. The graph of
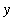 = F
= F
![``[2]](images/Antiderivative39.gif) is not a vertical shift of the other graphs. In general, any vertical shift of an antiderivative is sitll an antiderivative. This is a direct consequence of the fact that the derivative of a constant is zero. In the case of the specific functions in this example, any function of the form
is not a vertical shift of the other graphs. In general, any vertical shift of an antiderivative is sitll an antiderivative. This is a direct consequence of the fact that the derivative of a constant is zero. In the case of the specific functions in this example, any function of the form
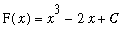 , where
, where
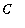 is a constant, is an antiderivative of
is a constant, is an antiderivative of
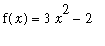 . In the notation for indefinite integrals,
. In the notation for indefinite integrals,
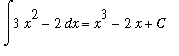
The
Antiderivative
Maplet
Further verification of this fact can be obtained with the
Antiderivative
maplet. If Maple is installed on your local computer, launch the maplet with the
Maplet Viewer; otherwise, use
MapleNet. Change the
Function
to
3*x^2-2
; leave
a
and
b
unchanged. Click the
Plot
button. The Plot Window will display a graph of the function
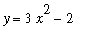 and one antiderivative
and one antiderivative
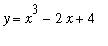 (the antiderivative that is zero at
(the antiderivative that is zero at
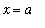 ). Now, click the check box for
Show class of antiderivatives
and then click the
Plot
button. The Plot Window now displays 20 antiderivatives of y=3*x^2-2. Notice how all 20 green curves are vertical shifts of the blue curve.
). Now, click the check box for
Show class of antiderivatives
and then click the
Plot
button. The Plot Window now displays 20 antiderivatives of y=3*x^2-2. Notice how all 20 green curves are vertical shifts of the blue curve.
The Antiderivative Rules
Every
Derivative Rule has a corresponding Antiderivative Rule.
![MATRIX([[Name, `Derivative Rule`, `Antiderivative Rule`, `Extra Conditions`], [___________________, __________________________, _________________________________, ______________], [Constant, Diff(k,x) ...](images/Antiderivative47.gif)
The restriction that
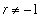 for the Power and Generalized Power Rules is necessary because we do not (yet) know any function whose derivative is
for the Power and Generalized Power Rules is necessary because we do not (yet) know any function whose derivative is
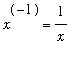 . The most likely candidate is
. The most likely candidate is
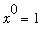 , but we know
, but we know
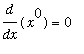 . If you ever forget this restriction and attempt to apply the Power or Generalized Power Rule with
. If you ever forget this restriction and attempt to apply the Power or Generalized Power Rule with
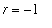 , division by
, division by
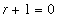 will remind you that this is not possible.
will remind you that this is not possible.
The antiderivative rules obtained from the quotient, product, and chain rules are not of interest at this time. The remaining examples in this lesson demonstrate the application of these rules.
Example 2:
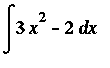
This is the same indefinite integral considered in Example 1. This time, let's determine the family of all antiderivatives using the Antiderivative Rules.
![MATRIX([[Int(3*x^2-2,x), `Original Problem`], [`` = Int(3*x^2,x)-Int(2,x), Difference*Rule], [`` = 3*Int(x^2,x)-2*Int(1,x), `Constant Multiple Rule (twice)`], [` ` = 3*(x^3/3+C[1])-2*(x+C[2...](images/Antiderivative55.gif)
Note that the constants could have been omitted when the Power and Identity Rules were applied provided the constant is included at the end.
Example 3:
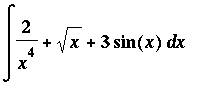
The Antiderivative Rules can be applied to evaluate this indefinite integral as follows:
![MATRIX([[Int(2/(x^4)+sqrt(x)+3*sin(x),x), `Original Problem`], [` ` = 2*Int(x^(-4),x)+Int(x^(1/2),x)+3*Int(sin(x),x), `Sum and Constant Multiple Rules`], [`` = 2*x^(-3)/(-3)+x^(3/2)/(3/2)+3*(-cos(...](images/Antiderivative57.gif)
To confirm this result simply compute the derivative of this answer:
| > |
ans3 := -2/(3*x^3) + 2/3*x^(3/2) - 3*cos(x) + C;
|
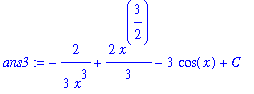
| > |
dF3 := Diff( ans3, x ):
dF3 = value( dF3 );
|
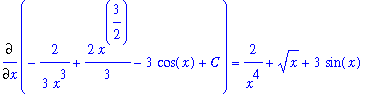
Because the derivative of our answer is the original function, the antiderivative is correct! That is,
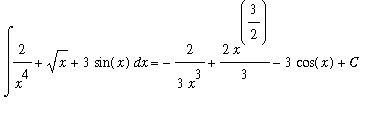 .
.
Note that if the constant
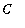 is omitted, then we would have
an
antiderivative. The same would be true if a specific value were assigned to
is omitted, then we would have
an
antiderivative. The same would be true if a specific value were assigned to
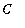 . When we say
the
antiderivative, we mean the family of all antiderivatives. Only when the constant is allowed to take on all real values have we found
the
antiderivative of the function.
. When we say
the
antiderivative, we mean the family of all antiderivatives. Only when the constant is allowed to take on all real values have we found
the
antiderivative of the function.
Example 4:
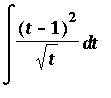
First, note that the dt indicates that the t is the independent variable in this problem. Before the antiderivative Rules can be applied to this problem it is necessary to expand and simplify the integrand. A full explanation of the steps to find all antiderivatives of the integrand are contained below:
![MATRIX([[Int((t-1)^2/sqrt(t),t), `Original Problem`], [`` = Int((t^2-2*t+1)/(t^(1/2)),t), `algebraic expansion`], [` ` = Int(t^(3/2)-2*t^(1/2)+t^(-1/2),t), `more algebra`], [` ...](images/Antiderivative64.gif)
To confirm this result, let
| > |
ans4 := 2/5*t^(5/2)-2*2/3*t^(3/2)+2*t^(1/2)+C;
|
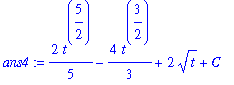
Then, computing the derivative with respect to
 :
:
| > |
dF4 := Diff( ans4, t ):
dF4 = value( dF4 );
`` = factor( value(dF4) );
|
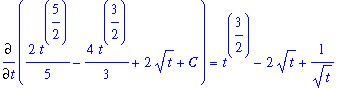
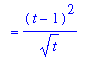
Thus,
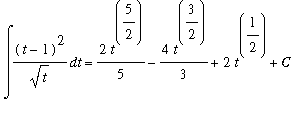 .
.
Example 5:
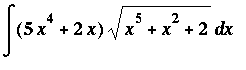
There is not much that can be done to rewrite the integrand of this indefinite integral in a form so that the Sum, Difference, and Constant Multiple Antiderivative Rules can be applied. But, notice that the coefficient of the square root is exactly the derivative of the expression inside the square root. This is the pattern that must exist to use the Generalized Power Rule with g(x) = x^5 + x^2 + 2 and r=1/2:
![MATRIX([[Int((5*x^4+2*x)*sqrt(x^5+x^2+2),x), `Original Problem`], [` ` = Int(diff(g(x),x)*g(x)^(1/2),x), `substitute: `*g(x) = x^5+x^2+2], [`` = g(x)^(3/2)/(3/2)+C, `Gen'l Power Rule, r=1...](images/Antiderivative71.gif)
Note that the constant appears in the problem when the integral sign disappears. And that it appears outside all other expressions.
As before, this result can be confirmed by differentiation:
| > |
ans5 := 2/3*(x^5+x^2+2)^(3/2)+C;
|
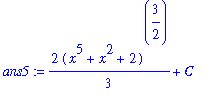
| > |
dF5 := Diff( ans5, x ):
dF5 = value( dF5 );
|
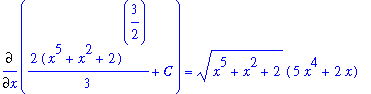
Great! This shows that
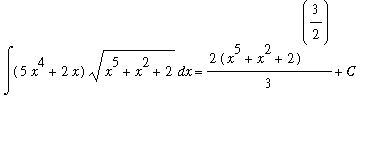 .
.
Example 6:
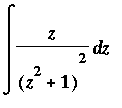
Compare this integrand to the integrand in Example 4. Note that expanding the denominator of the integrand does not help to find the antiderivative. Instead, it should be noted that if the numerator is 2*z then it would be the derivative of ( z^2+1 ). Then, writing the 1/(z^2+1)^2 with a negative exponent, the Generalized Power Rule could be used to evaluate this indefinite integral. Here is the complete evaluation:
![MATRIX([[Int(z/((z^2+1)^2),z), `Original Problem`], [`` = Int(z*(z^2+1)^(-2),z), `rewrite with negative exponent`], [` ` = 1/2*Int(2*z*(z^2+1)^(-2),z), `multiply by `*1 = 1/2*2], [` ` ...](images/Antiderivative76.gif)
Lesson Summary
The process of undoing differentiation is called antidifferentiation or indefinite integration. Because the derivative of a constant is zero,
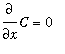 , if one antiderivative can be found, then adding an arbitrary constant produces an infinite family of antiderivatives. The Antiderivative Rules are obtained by reversing a
Differentiation Rule. One nice property of antiderivatives is that it is always possible to use differentiation to check that an antiderivative is correct.
, if one antiderivative can be found, then adding an arbitrary constant produces an infinite family of antiderivatives. The Antiderivative Rules are obtained by reversing a
Differentiation Rule. One nice property of antiderivatives is that it is always possible to use differentiation to check that an antiderivative is correct.
What's Next?
The ability to find antiderivatives and evaluate indefinite integrals is fundamental to the final two units of this course. The
Antiderivative
maplet [
Maplet Viewer][
MapleNet] can assist with your development of a better understanding of the geometric relationship between a function and its antiderivatives. Use the online practice sessions for this lesson to improve your skills. The general practice session should be mastered prior to attempting the
online homework assignment. The
assigned problems from the text should also be completed.
The next lesson applies the search for antiderivatives to the search for solutions to
Differential Equations. This lesson is a very brief introduction to an important topic in mathematics. Many of you will probably take a
course in Differential Equations after you complete the Calculus sequence.
![]() if
if
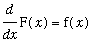 for all
for all
![]() in
in
![]() .
.
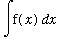 , read "the indefinite integral of
, read "the indefinite integral of
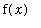 with respect to
with respect to
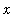 ", the first symbol (an elongated S) is called the
integral sign
, the
integrand
is
", the first symbol (an elongated S) is called the
integral sign
, the
integrand
is
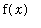 , and
, and
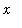 is the
variable of integration
. The integral sign and the dx should be viewed as a matched pair -- much like left- and right-parentheses.
is the
variable of integration
. The integral sign and the dx should be viewed as a matched pair -- much like left- and right-parentheses.
![]() ) and compare this result with f on the interval
) and compare this result with f on the interval
![]()
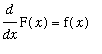 if and only if
if and only if
![]() .
.
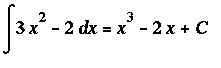
![[Maple Plot]](images/Antiderivative29.gif)
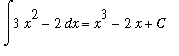
![MATRIX([[Name, `Derivative Rule`, `Antiderivative Rule`, `Extra Conditions`], [___________________, __________________________, _________________________________, ______________], [Constant, Diff(k,x) ...](images/Antiderivative47.gif)
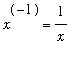 . The most likely candidate is
. The most likely candidate is
 . If you ever forget this restriction and attempt to apply the Power or Generalized Power Rule with
. If you ever forget this restriction and attempt to apply the Power or Generalized Power Rule with
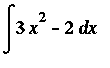
![MATRIX([[Int(3*x^2-2,x), `Original Problem`], [`` = Int(3*x^2,x)-Int(2,x), Difference*Rule], [`` = 3*Int(x^2,x)-2*Int(1,x), `Constant Multiple Rule (twice)`], [` ` = 3*(x^3/3+C[1])-2*(x+C[2...](images/Antiderivative55.gif)
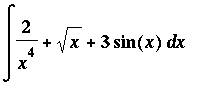
![MATRIX([[Int(2/(x^4)+sqrt(x)+3*sin(x),x), `Original Problem`], [` ` = 2*Int(x^(-4),x)+Int(x^(1/2),x)+3*Int(sin(x),x), `Sum and Constant Multiple Rules`], [`` = 2*x^(-3)/(-3)+x^(3/2)/(3/2)+3*(-cos(...](images/Antiderivative57.gif)
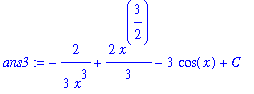
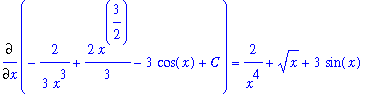
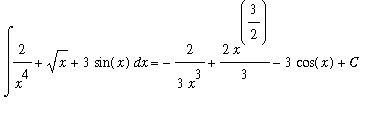 .
.
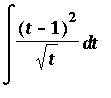
![MATRIX([[Int((t-1)^2/sqrt(t),t), `Original Problem`], [`` = Int((t^2-2*t+1)/(t^(1/2)),t), `algebraic expansion`], [` ` = Int(t^(3/2)-2*t^(1/2)+t^(-1/2),t), `more algebra`], [` ...](images/Antiderivative64.gif)
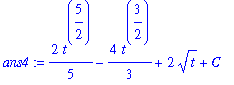
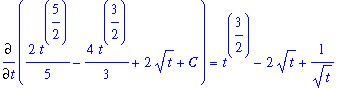
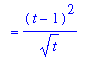
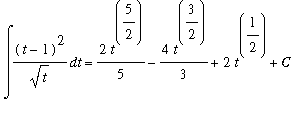 .
.
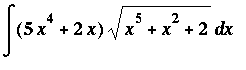
![MATRIX([[Int((5*x^4+2*x)*sqrt(x^5+x^2+2),x), `Original Problem`], [` ` = Int(diff(g(x),x)*g(x)^(1/2),x), `substitute: `*g(x) = x^5+x^2+2], [`` = g(x)^(3/2)/(3/2)+C, `Gen'l Power Rule, r=1...](images/Antiderivative71.gif)
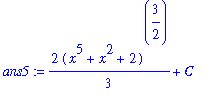
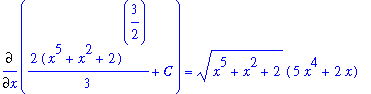
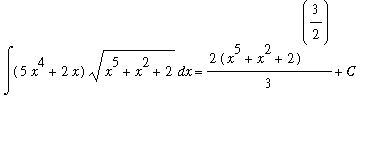 .
.
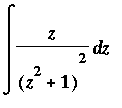
![MATRIX([[Int(z/((z^2+1)^2),z), `Original Problem`], [`` = Int(z*(z^2+1)^(-2),z), `rewrite with negative exponent`], [` ` = 1/2*Int(2*z*(z^2+1)^(-2),z), `multiply by `*1 = 1/2*2], [` ` ...](images/Antiderivative76.gif)
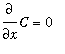 , if one antiderivative can be found, then adding an arbitrary constant produces an infinite family of antiderivatives. The Antiderivative Rules are obtained by reversing a
, if one antiderivative can be found, then adding an arbitrary constant produces an infinite family of antiderivatives. The Antiderivative Rules are obtained by reversing a