MVTIntegral.mws
Mean Value Theorem for Integrals
| > |
restart;
with( plots ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Lesson Overview
The Mean Value Theorem for Integrals is a direct consequence of the
Mean Value Theorem (for Derivatives) and the First
Fundamental Theorem of Calculus. In words, this result is that a continuous function on a closed, bounded interval has at least one point where it is equal to its average value on the interval. Geometrically, this means that the area under the graph of a continuous function on a closed, bounded interval is equal to the area of a rectangle whose base is the length of the interval and height is the value of the integrand at some point in the interval.
The
FunctionAverage
maplet [
Maplet Viewer][
MapleNet] can be used to plot a function, setup the definite integral for the average value on an interval, and visualize the conclusion of the MVT for Integrals. This maplet is built around the
FunctionAverage
command in the
Student[Calculus1]
package.
Theorem (Mean Value Theorem for Integrals)
If f is a continuous function on the closed, bounded interval [
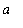 ,
,
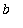 ], then there is at least one number
], then there is at least one number
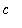 in (
in (
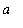 ,
,
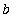 ) for which
) for which
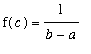
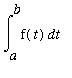 .
.
Proof:
The proof of the MVT for Integrals is an application of the MVT for Integrals with an appropriate choice of the function. Define the function F so that
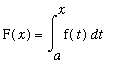 for every value of
for every value of
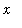 in [
in [
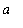 ,
,
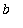 ].
].
The First
Fundamental Theorem of Calculus tells us that F is continuous on [
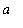 ,
,
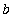 ], is differentiable on (
], is differentiable on (
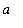 ,
,
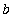 ), and
), and
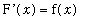 . These are exactly the conditions needed to apply the
Mean Value Theorem for Derivatives to F on [
. These are exactly the conditions needed to apply the
Mean Value Theorem for Derivatives to F on [
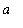 ,
,
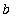 ]. That is, there is at least one point
]. That is, there is at least one point
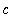 in (
in (
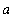 ,
,
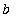 ) for which
) for which
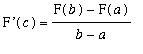 .
.
Now, from the definition of F,
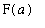 =
=
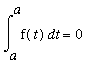
and
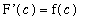 .
.
Thus,
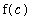 =
=
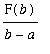 =
=
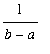
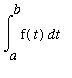 .
.
Example 1: Average Value of a Function
Let f be a function defined on the interval [
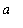 ,
,
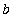 ]. Consider a regular partition of [
]. Consider a regular partition of [
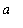 ,
,
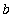 ] into
] into
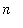 subintervals with endpoints
subintervals with endpoints
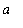 =
=
![x[0]](images/MVTIntegral36.gif) <
<
![x[1]](images/MVTIntegral37.gif) < .. <
< .. <
![x[n-1]](images/MVTIntegral38.gif) <
<
![x[n]](images/MVTIntegral39.gif) =
=
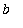 ,
,
that is, for each
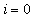 , 1, ..,
, 1, ..,
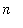 , define
, define
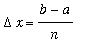 and
and
![x[i] = a+i*Delta*x](images/MVTIntegral44.gif)
The average of
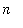 function values,
function values,
![f(x[1])](images/MVTIntegral46.gif) ,
,
![f(x[2])](images/MVTIntegral47.gif) , ...,
, ...,
![f(x[n])](images/MVTIntegral48.gif) , is
, is
![mu = (f(x[1])+f(x[2])+`..`+f(x[n]))/n](images/MVTIntegral49.gif)
![`` = Sum(f(x[i])/n,i = 1 .. n)](images/MVTIntegral50.gif)
![`` = Sum(f(x[i]),i = 1 .. n)](images/MVTIntegral51.gif)
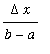
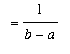
![Sum(f(x[i])*Delta*x,i = 1 .. n)](images/MVTIntegral54.gif) .
.
Observe that in the final two steps, the definition of
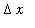 has been used to write
has been used to write
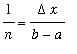 and the constant
and the constant
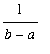 has been factored out of the sum.
has been factored out of the sum.
The sum in this last expression is a Riemann sum. If the number of data points is allowed to increase without bound a definite integral can be identified:
![Limit(Sum(f(x[i])*Delta*x,i = 1 .. n),n = infinity)](images/MVTIntegral58.gif) =
=
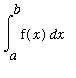 .
.
This is the motivation for the definition of the average value of a function:
Definition (Average Value of a Function)
Let f be a continuous function on a closed, bounded interval [
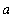 ,
,
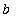 ]. The
average value of
f
on
[
]. The
average value of
f
on
[
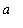 ,
,
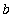 ] is
] is
![f[avg]](images/MVTIntegral64.gif) =
=
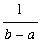
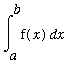 .
.
The FunctionAverage command in Maple's Student[Calculus1] package
Example 2: Hypotheses of MVT Satisfied
The function
| > |
f2 := piecewise( x<0, 0, x<1, x, exp(1-x) ):
f(x) = f2;
|
![f(x) = PIECEWISE([0, x < 0],[x, x < 1],[exp(1-x), otherwise])](images/MVTIntegral67.gif)
is continuous for all real numbers. In particular, the MVT for Integrals applies on the interval [ -5, 5 ].
| > |
plot( f2, x=-5..5, axes=framed );
|
![[Maple Plot]](images/MVTIntegral68.gif)
The average value of f on [ -5, 5 ] is
| > |
f2_avg := FunctionAverage( f2, x=-5..5, output=integral ):
f[avg] = f2_avg;
`` = value( f2_avg );
`` = evalf( f2_avg );
|
![f[avg] = 1/10*Int(PIECEWISE([0, x < 0],[x, x < 1],[exp(1-x), otherwise]),x = -5 .. 5)](images/MVTIntegral69.gif)
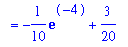
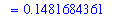
When the average value is included in the plot of the function, the shaded area below the average value should be equal to the area under the function.
| > |
FunctionAverage( f2, x=-5..5, output=plot,
averageoptions=[color=cyan,filled=true],
view=[DEFAULT,0..1] );
|
![[Maple Plot]](images/MVTIntegral72.gif)
The graph suggests that there are two points in the interval ( -5, 5 ) where the function value is equal to the average value of the function on [ -5, 5 ]. These two points are
| > |
s2 := solve( f2=value(f2_avg), {x} ):
s2;
|
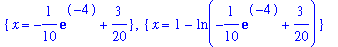
or, numerically,
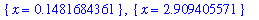
These values are consistent with the graph.
Example 3: Hypotheses of MVT Not Satisfied
The piecewise constant function
| > |
f3 := piecewise( x<0, -1, x<2, 2, 1 ):
f(x) = f3;
|
![f(x) = PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise])](images/MVTIntegral75.gif)
has jump discontinuities at
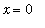 and
and
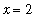 . Because f is not continuous at
. Because f is not continuous at
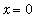 or
or
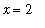 , the MVT for Integrals does not apply on the interval [ -3, 3 ].
, the MVT for Integrals does not apply on the interval [ -3, 3 ].
| > |
plot( f3, x=-3..3, discont=true );
|
![[Maple Plot]](images/MVTIntegral80.gif)
To understand why the conclusion of the MVT for Integrals is not satisfied, observe that the average value of f on [ -3, 3 ] is
| > |
f3_avg := FunctionAverage( f3, x=-3..3, output=integral ):
f3_avg = value( f3_avg );
|
![1/6*Int(PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise]),x = -3 .. 3) = 1/3](images/MVTIntegral81.gif)
Since the function values are -1, 1, and 2, it is clear that there are no points on ( -3, 3 ) where
![f(x) = f[avg]](images/MVTIntegral82.gif) =
=
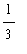 .
.
| > |
FunctionAverage( f3, x=-3..3, output=plot,
averageoptions=[color=cyan,filled=true],
view=[DEFAULT,-1..2] );
|
![[Maple Plot]](images/MVTIntegral84.gif)
| > |
solve( f3=value(f3_avg), {x} );
|
Note that the average value of the function on [ -1, 3 ] is
| > |
f3_avg2 := FunctionAverage( f3, x=-1..3, output=integral ):
f3_avg2 = value( f3_avg2 );
|
![1/4*Int(PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise]),x = -1 .. 3) = 1](images/MVTIntegral85.gif)
Now, since the average value of the function on [ -1, 3 ] is one of the values of this function, there are points where the function value coincides with the average value on [ -1, 3 ]. Graphically,
| > |
FunctionAverage( f3, x=-1..3, output=plot,
averageoptions=[color=cyan,filled=true],
view=[DEFAULT,-1..2] );
|
![[Maple Plot]](images/MVTIntegral86.gif)
And, algebraically,
| > |
solve( f3=value(f3_avg2), {x} );
|
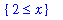
While the MVT for Integrals does not apply on either [ -3, 3 ] or [ -1, 3 ], it is not a contradiction to find a case where the conclusion holds even when the hypotheses are false. (In terms of boolean logic: False implies True is a True statement.)
Example 4: Human Respiration
The essential life function of breathing is cyclic. At rest a fit human will complete approximately 10 full respiratory cycles every minute. The maximum rate of air flow into the lungs is about one-half liter per second. Based on these assumptions the rate of air flow into the lungs can be modeled by the function
| > |
num_resp_cycle_per_minute := 10;
max_rate_of_air_flow := 1/2;
|
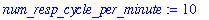
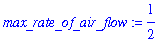
| > |
rate := max_rate_of_air_flow
* sin( 2*Pi*x * (num_resp_cycle_per_minute/60) ):
f(t) = rate;
|
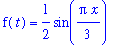
The volume (in liters) of air in the lungs at time
 (in seconds) is
(in seconds) is
| > |
VOL := Int( rate, x=0..t ):
vol := value( VOL ):
V(t) = VOL;
`` = vol;
|
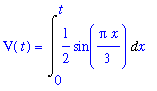
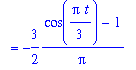
The relationship between the rate of air flow and the volume of air in the lungs is clearly shown in the following plot.
| > |
P1 := plot( [vol, eval(rate,x=t)], t=0..30,
title="Volume of Air in Lungs",
legend=["volume (L)","rate of air flow (L/s)"] ):
P1;
|
![[Maple Plot]](images/MVTIntegral94.gif)
Observe that the volume is periodic, with period 6 seconds, and that the maximum amount of air in the lungs is
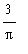 L, or approximately 0.9549 L. The maximum occurs every time
L, or approximately 0.9549 L. The maximum occurs every time
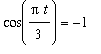 ; the minimum value, 0 L, is attained every time
; the minimum value, 0 L, is attained every time
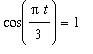 . (During times of exercise and other stresses respiration increases; the maximum lung capacity is about 3.7 L.)
. (During times of exercise and other stresses respiration increases; the maximum lung capacity is about 3.7 L.)
The average amount of air in the lungs during one complete respiration cycle is
| > |
avg_vol := FunctionAverage( vol, t=0..6, output=integral ):
V[avg] = avg_vol;
`` = value( avg_vol );
`` = evalf( avg_vol );
|
![V[avg] = 1/6*Int(-3/2*(cos(1/3*Pi*t)-1)/Pi,t = 0 .. 6)](images/MVTIntegral98.gif)
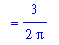
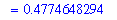
The average amount of air in the lungs during each respiratory cycle (while at rest) is a little under
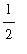 L.
L.
| > |
P2 := plot( value(avg_vol), x=0..30,
color=blue, legend="average value of volume (L)" ):
P3 := plot( value(avg_vol), x=0..30,
color=cyan, legend="", filled=true ):
display( P1,P3 );
|
![[Maple Plot]](images/MVTIntegral102.gif)
Note that the average value is not the maximum rate of air flow. Numerically the two quantities are close, but the values (and units) are different.
Lesson Summary
The Mean Value Theorem for Integrals is obtained when the
Mean Value Theorem (for Derivatives) is applied to the function
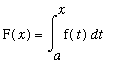 on the interval [
on the interval [
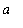 ,
,
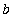 ]. This version of the MVT provides conditions when the function is ensured to take on the average value of the function somewhere in the interval. That is, when there is guaranteed to be at least number c in (
]. This version of the MVT provides conditions when the function is ensured to take on the average value of the function somewhere in the interval. That is, when there is guaranteed to be at least number c in (
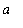 ,
,
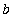 ) where
) where
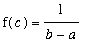
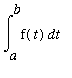 .
.
What's Next?
Now that you have completed this lesson, you should practice computing the average value of a function and knowing when the MVT for Integrals can and cannot be appled. The
online homework assignment includes practice sessions for these skills as well as a general practice session for problems related to this lesson, and a graded homework assignment. Also, complete the
assigned problems from the text. Remember to use the
FunctionAverage
maplet [
Maplet Viewer][
MapleNet] to assist with some of the average value computations.
Quiz 9 contains questions from the
Mean Value Theorem for Integrals and
Area of a Plane Region lessons.
The remaining applications in this unit ---
Volume of a Solid,
Length of a Plane Curve, and
Work --- can be covered in any order.
![]() ,
,
![]() ], then there is at least one number
], then there is at least one number
![]() in (
in (
![]() ,
,
![]() ) for which
) for which
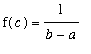
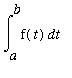 .
.
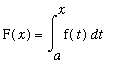 for every value of
for every value of
![]() in [
in [
![]() ,
,
![]() ].
].
![]() ,
,
![]() ], is differentiable on (
], is differentiable on (
![]() ,
,
![]() ), and
), and
![]() . These are exactly the conditions needed to apply the
Mean Value Theorem for Derivatives to F on [
. These are exactly the conditions needed to apply the
Mean Value Theorem for Derivatives to F on [
![]() ,
,
![]() ]. That is, there is at least one point
]. That is, there is at least one point
![]() in (
in (
![]() ,
,
![]() ) for which
) for which
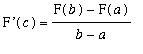 .
.
![]() =
=
![]() .
.
![]() =
=
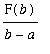 =
=
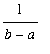
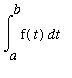 .
.
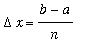 and
and
![mu = (f(x[1])+f(x[2])+`..`+f(x[n]))/n](images/MVTIntegral49.gif)
![`` = Sum(f(x[i])/n,i = 1 .. n)](images/MVTIntegral50.gif)
![`` = Sum(f(x[i]),i = 1 .. n)](images/MVTIntegral51.gif)
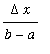
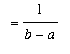
![Sum(f(x[i])*Delta*x,i = 1 .. n)](images/MVTIntegral54.gif) .
.
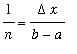 and the constant
and the constant
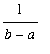 has been factored out of the sum.
has been factored out of the sum.
![Limit(Sum(f(x[i])*Delta*x,i = 1 .. n),n = infinity)](images/MVTIntegral58.gif) =
=
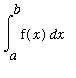 .
.
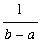
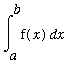 .
.
![f(x) = PIECEWISE([0, x < 0],[x, x < 1],[exp(1-x), otherwise])](images/MVTIntegral67.gif)
![[Maple Plot]](images/MVTIntegral68.gif)
![f[avg] = 1/10*Int(PIECEWISE([0, x < 0],[x, x < 1],[exp(1-x), otherwise]),x = -5 .. 5)](images/MVTIntegral69.gif)
![[Maple Plot]](images/MVTIntegral72.gif)
![f(x) = PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise])](images/MVTIntegral75.gif)
![[Maple Plot]](images/MVTIntegral80.gif)
![1/6*Int(PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise]),x = -3 .. 3) = 1/3](images/MVTIntegral81.gif)
![[Maple Plot]](images/MVTIntegral84.gif)
![1/4*Int(PIECEWISE([-1, x < 0],[2, x < 2],[1, otherwise]),x = -1 .. 3) = 1](images/MVTIntegral85.gif)
![[Maple Plot]](images/MVTIntegral86.gif)
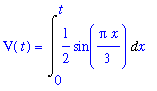

![[Maple Plot]](images/MVTIntegral94.gif)
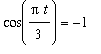 ; the minimum value, 0 L, is attained every time
; the minimum value, 0 L, is attained every time
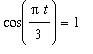 . (During times of exercise and other stresses respiration increases; the maximum lung capacity is about 3.7 L.)
. (During times of exercise and other stresses respiration increases; the maximum lung capacity is about 3.7 L.)
![V[avg] = 1/6*Int(-3/2*(cos(1/3*Pi*t)-1)/Pi,t = 0 .. 6)](images/MVTIntegral98.gif)
![[Maple Plot]](images/MVTIntegral102.gif)
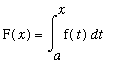 on the interval [
on the interval [
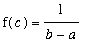
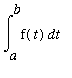 .
.