Area.mws
Area of a Plane Region
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
Area is used in the
Riemann Sums lesson to begin the development of the
Definite Integral. In that context all areas are computed as explicit limits. The
Fundamental Theorems of Calculus and
Evaluating Definite Integrals lessons provide efficient tools for the evaluating a definite integral. The essential idea developed in this lesson is summarized as
slice, approximate, limit, evaluate.
This is the general process used to express the area of a plane region as a definite integral and evaluate the integral. This same process is used in the other applications considered in this unit ---
Volume of a Solid,
Length of a Plane Curve, and
Work --- as well as many other applications of the definite integral.
Maplet Request:
Area
It would be nice to have an
Area
maplet. This maplet would allow the user to indicate if the region is vertically or horizontally simple. For vertically simple regions, the top and bottom would be entered as y=(function) and the endpoints would be x=(number). For horizontally simple regions, the left and right would be x=(function) and the endpoints would be y=(number). Visually, it would be ideal to have a slider located under (vert. simple) or to the left (horiz. simple) of the plot of the region. As the slider moves, the corresponding slice of the area would be highlighted. (I am thinking that the region would be filled.) If the slider idea is too difficult or not possible, then I would like to show the slices as an animation. The number of frames could be entered by the user (a slider for the # of frames would prevent users from entering too many frames).
Example 1: Region Between Two Curves
The region bounded by the graphs of
| > |
top1 := sqrt(x):
y = top1;
|
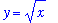
and
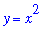
on the interval [ 0, 1 ] is shown in the following plot
| > |
plot( [top1,bot1], x=0..1, color=[red,blue], legend=["top: y=sqrt(x)","bottom: y=x^2"] );
|
![[Maple Plot]](images/Area3.gif)
The area of this region is given by the definite integral
| > |
A1 := Int( top1-bot1, x=0..1 ):
Area = A1;
`` = value( A1 );
|
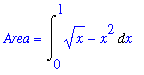
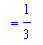
Example 2: Positive and Negative Area
The area between the graphs of
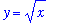
and
| > |
g2 := exp(-3*x):
y = g2;
|
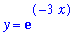
on the interval [ 0, 1 ] consists of two parts, as shown in the following plot.
| > |
P0 := plot( [[1,exp(-3)],[1,1]], color=green, legend=["x = 1"] ):
P1 := plot( [f2,g2], x=0..1, color=[red,blue], legend=["y = sqrt(x)", "y = exp(-3*x)"] ):
display( [P1,P0] );
|
![[Maple Plot]](images/Area8.gif)
The first piece of the area has the exponential curve as the upper boundary and the square root as the lower boundary; after the curves intersect, these roles are reversed. The following plot emphasizes this
| > |
P2 := plot( [ max(f2,g2), min(f2,g2) ], x=0..1, color=[yellow,cyan], legend=["Top", "Bottom"], thickness=5 ):
display( [ P1, P2, P0] );
|
![[Maple Plot]](images/Area9.gif)
The definite integral for the total area enclosed
| > |
A1 := Int( g2-f2, x=0..T ):
A2 := Int( f2-g2, x=T..1 ):
Area = A1 + A2;
|

where
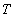 is the
is the
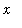 -coordinate of the point where the two curves intersect:
-coordinate of the point where the two curves intersect:
| > |
T_exact := solve( f2=g2, x ):
T_approx := evalf( T_exact ):
T = T_exact;
`` = T_approx;
|
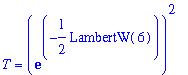

| > |
Area = A1 + A2;
`` = value( eval( A1 + A2, T=T_approx ) );
|
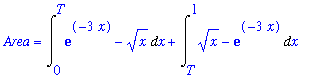
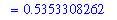
Example 3: Horizontal Slices
The region bounded by the horizontal line
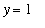 ,
,
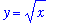
and
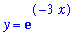
lies above the graph of
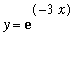 for x in [ 0,
for x in [ 0,
 ] and above the graph of
] and above the graph of
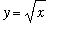 for x in [
for x in [
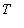 , 1 ]. That is, using vertical slices, the area can be represented as
, 1 ]. That is, using vertical slices, the area can be represented as
| > |
A_v := Int( 1-g2, x=0..T ) + Int( 1-f2, x=T..1 ):
Area = A_v;
`` = value( eval( A_v, T=T_approx ) );
|
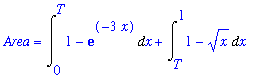

This area can be represented as a single definite integral if horizontal slices are used. To work with horizontal slices requires writing the left and right boundaries as functions of
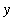 . The left boundary is formed by the graph of
. The left boundary is formed by the graph of
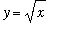 , or
, or
| > |
left3 := solve( y=f2, x ):
x = left3;
|
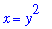
The right boundary is formed by the graph of
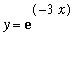 , or
, or
| > |
right3 := solve( y=g2, x ):
x = right3;
|
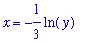
Let
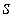 denote the y-coordinate of the intersection point of the two graphs:
denote the y-coordinate of the intersection point of the two graphs:
| > |
S_exact := simplify( eval( g2, x=T_exact ) ):
S_approx := evalf( S_exact ):
S = S_exact;
`` = S_approx;
|
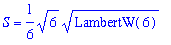
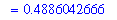
Note that this value could also be obtained by solving the equation
| > |
q1 := left3 = right3:
q1;
|
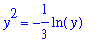
for
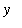 :
:
| > |
q2 := solve( q1, y ):
q2 = simplify( q2 );
|
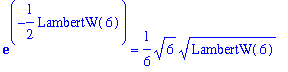
The region with the left, right, and top boundaries highlighted is
| > |
P3 := implicitplot( x=left3, x=0..1, y = S_approx..1, color=yellow, legend="Left", thickness=5 ):
P4 := implicitplot( x=right3, x=0..1, y = S_approx..1, color=cyan, legend="Right", thickness=5 ):
P5 := plot( 1, x=0..1, color=coral, legend="Top", thickness=5 ):
display( [ P1, P3, P4, P5 ] );
|
![[Maple Plot]](images/Area37.gif)
The area of this region can now be written as a single definite integral:
| > |
A_h := Int( left3-right3, y=S..1 ):
Area = A_h;
`` = value( eval( A_h, S=S_approx ) );
|
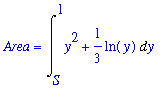

Fortunately, the two different approaches to finding the area of this region agree!
Example 4: Area of an Ellipse
The area of an ellipse with axes of length a and b is the area of region bounded by the graph of
| > |
q3 := (x/a)^2 + (y/b)^2 = 1:
q3;
|
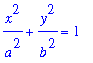
| > |
P6 := implicitplot( eval(q3,[a=1,b=2]), x=-3..3, y=-3..3, scaling=constrained, numpoints=1000, tickmarks=[0,0] ):
P7 := textplot( [ [1/2,0.05,"a"], [0.05,1,"b"] ], font=[TIMES,ITALIC,15], align={ABOVE,RIGHT} ):
display( [ P6, P7 ] );
|
![[Maple Plot]](images/Area41.gif)
| > |
top4 := solve( q3, y )[1];
|
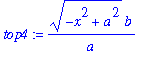
| > |
right4 := solve( q3, x )[1];
|
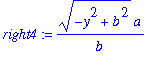
| > |
A_ell_v := 4 * Int( top4, x=0..a ):
A_ellipse = A_ell_v;
|
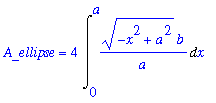
While this integral cannot be evaluated using the integration techniques discussed in this course, it can be evaluated. The key is to factor the b/a out of the integal and to observe that the remaining definite integral
| > |
q4 := Int( sqrt( a^2-x^2 ), x=0..a ):
q4;
|
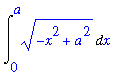
is one fourth of the area of a circle with radius a. That is,
| > |
q4 = value( q4 ) assuming a>0;
|
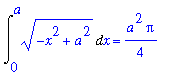
As a result, the area of an ellipse with radii a and b is
![A[ellipse]](images/Area47.gif) = 4
= 4
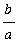 (
(
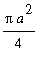 ) =
) =
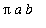 :
:
Note that this formula does reduce to the area of a circle with radius
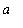 when
when
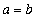 . Note also that this result could have been obtained with horizontal slices. The definite integral for that scenario is
. Note also that this result could have been obtained with horizontal slices. The definite integral for that scenario is
| > |
A_ell_h := 4 * Int( right4, y=0..b ):
A_ellipse = A_ell_h;
|
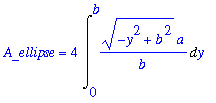
Evaluation of this integral is almost identical to the one encountered with vertical slices. Factor out
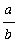 , recognize the remaining integral as one-fourth of the area of a circle with radius
, recognize the remaining integral as one-fourth of the area of a circle with radius
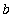 , then simplify to obtain:
, then simplify to obtain:
| > |
A_ellipse = A_ell_h;
`` = value( A_ell_h ) assuming a>0, b>0;
|
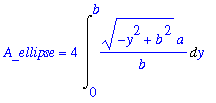
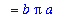
As expected, the two different slicing methods lead to the same answer.
Lesson Summary
The computation of areas is one of the fundamental applications of the definite integral. A definite integral for the area of a plane region can be found by adding up an appropriate collection of infinitely thin horizontal or vertical slices. The integrand is the length of each slice and the limits of integration correspond to the smallest and largest values of the independent variable that describe the region.
The area of a v
ertically simple region
described by
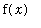 <=
<=
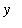 <=
<=
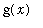 for all
for all
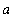 <=
<=
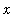 <=
<=
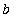
is
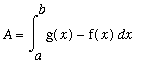 .
.
The area of a
horizontally simple region
described by
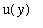 <=
<=
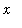 <=
<=
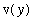 for all
for all
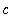 <=
<=
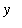 <=
<=
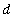
is
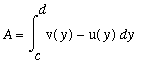 .
.
While it is important to be able to evaluate a definite integral for an area, the step that requires real skill and understanding is coming up with the definite integral.
What's Next?
Prior to completing the
online homework assignment, you should dedicate time to practicing setting up definite integrals for the area of a plane region. The
assigned problems from the text provide additional assessment of your mastery of your ability to set up definite integrals for areas.
The next lesson in this unit considers area in the graphical interpretation of the Mean Value Theorem for Integrals. In this lesson the average value of a function will be developed using the slice, approximate, limit, evaluate process. The remaining lessons in this unit,
Volume of a Solid,
Length of a Plane Curve, and
Work, use the same general process to develop additional geometric and physical properties.
![]()
![]()
![[Maple Plot]](images/Area3.gif)
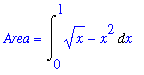
![]()
![[Maple Plot]](images/Area8.gif)
![[Maple Plot]](images/Area9.gif)

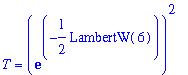
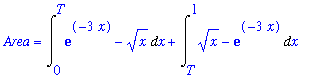
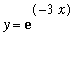 for x in [ 0,
for x in [ 0,
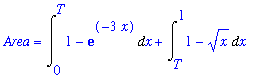
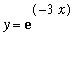 , or
, or
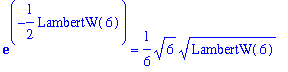
![[Maple Plot]](images/Area37.gif)
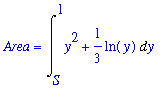
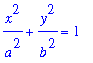
![[Maple Plot]](images/Area41.gif)
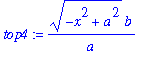
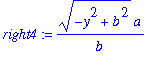
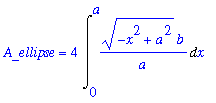
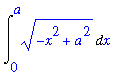
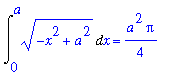
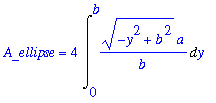
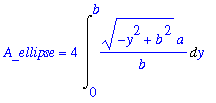
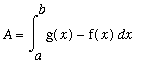 .
.
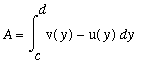 .
.