FundamentalTheorems.mws
Fundamental Theorems of Calculus
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
This is the lesson in which the connection between definite and indefinite integrals is exposed. At this point
Indefinite Integrals, antiderivatives, are obtained by reversing the differentiation process.
Definite Integrals arise as limits of Riemann sums and provide information about the area of a region.
There are two Fundamental Theorems of Calculus. The definite integral can be used to define new functions. The First Fundamental Theorem of Calculus shows how to differentiate this type of function.
First Fundamental Theorem of Calculus
Let f be a continuous function on an interval
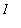 that contains
that contains
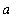 . Define the function F on the interval
. Define the function F on the interval
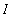 in terms of the definite integral
in terms of the definite integral
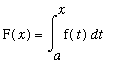 .
.
Then i) F is differentiable on
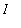 and ii)
and ii)
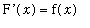 for all
for all
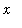 in
in
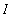 .
.
One consequence of this theorem is that
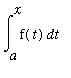 is an antiderivative of f.
is an antiderivative of f.
The Second Fundamental Theorem of Calculus shows how antiderivatives can be used to evaluate a definite integral.
Second Fundamental Theorem of Calculus
Let F be any antiderivative of f on an interval
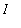 , that is,
, that is,
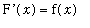 for all
for all
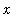 in
in
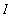 . Then
. Then
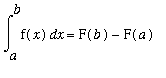 .
.
With this result it is no longer necessary to use limits or geometry to evaluate definite integrals.
First Fundamental Theorem of Calculus
Let f be a continuous function on an interval
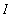 that contains
that contains
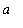 . Define the function F on the interval
. Define the function F on the interval
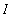 in terms of the definite integral
in terms of the definite integral
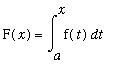 .
.
Then i) F is differentiable on
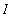 and ii)
and ii)
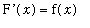 for all
for all
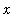 in
in
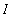 .
.
Proof
The proof of this theorem uses the
Precise Definition of the Derivative to compute `F'`(x).
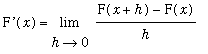
=
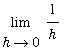 (
(
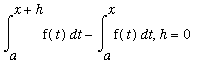 )
)
=
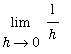 (
(
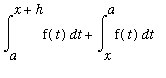 )
)
=
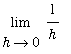
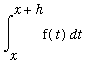
Observe that, when
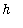 is small,
is small,
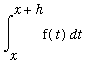 is can be estimated as the "area" of the rectangle with base
is can be estimated as the "area" of the rectangle with base
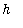 and height
and height
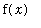 . That is,
. That is,
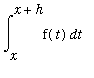 is approximately
is approximately
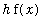 . Therefore,
. Therefore,
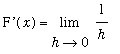
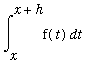
=
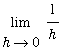 (
(
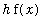 )
)
=
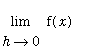
=
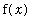 .
.
Because this limit exists (for all x in I), F is differentiable on I.
Notes
-
A rigorous proof uses the fact that
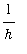
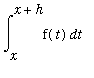 is the average value of f on [
is the average value of f on [
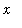 ,
,
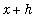 ] and the
Mean Value Theorem for Integrals to complete the evaluation of the limit in the computation of F'.
] and the
Mean Value Theorem for Integrals to complete the evaluation of the limit in the computation of F'.
-
Another way to estimate
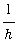
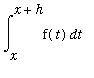 is to use Upper and Lower Riemann sums with 1 subinterval to obtain upper and lower bounds for the integral. Let
is to use Upper and Lower Riemann sums with 1 subinterval to obtain upper and lower bounds for the integral. Let
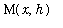 and
and
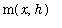 denote the largest and smallest values of f on the interval [
denote the largest and smallest values of f on the interval [
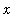 ,
,
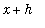 ]. (These values exist because f is continuous on this interval.) Then,
]. (These values exist because f is continuous on this interval.) Then,
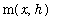 <=
<=
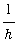
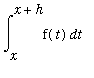 <=
<=
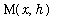 .
.
With the observation that
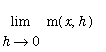 =
=
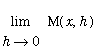 =
=
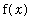 , the final steps in the evaluation of
, the final steps in the evaluation of
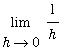
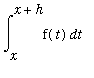 can be completed by an application of the
Sandwich Theorem for Limits.
can be completed by an application of the
Sandwich Theorem for Limits.
-
The fact that F' = f means that F is an antiderivative of f. Heretofore, the derivations and definitions of indefinite and definite integrals provided no reason to expect there to be any connection between these topics.
Example 1
Consider the function
| > |
f1 := t^3:
F1 := Int( f1, t=1..x ):
F(x) = F1;
|
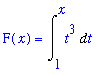
By the First Fundamental Theorem of Calculus, it is known that F is a differentiable function and
| > |
dF1 := eval( f1, t=x ):
`F'`(x) = dF1;
|
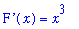
At the same time, we know that the family of antiderivatives of
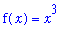
is
| > |
FF1 := Int( dF1, x ):
FF1 = value( FF1 ) + C;
|
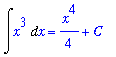
This means that the function F(x) must be one of antiderivatives of
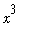 :
:
| > |
F(x) = value( FF1 ) + C;
|
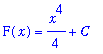
for some choice of the constant
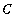 .
.
To determine the appropriate value for
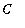 , note that
, note that
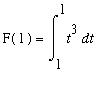 = 0.
= 0.
This condition will be satisfied by exactly one antiderivative. The equation that selects the correct antiderivative is
| > |
eq1 := eval( value( FF1 ) + C, x=1 ) = 0:
eq1;
|
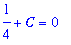
This equation is simple to solve:
| > |
C1 := isolate( eq1, C ):
C1;
|
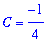
| > |
F(x) = eval( value( FF1 ) + C, C1 );
|
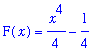
Example 2
Consider the function
| > |
f2 := cos( t^2 ):
F2 := Int( f2, t=0..sqrt(x) ):
F(x) = F2;
|
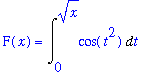
defined for all
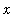 >= 0. Find a formula for the derivative,
>= 0. Find a formula for the derivative,
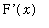 , that is valid for all
, that is valid for all
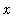 >= 0.
>= 0.
This function is a little more complicated. Before starting to compute the derivative, let's see a plot of the function.
![[Maple Plot]](images/FundamentalTheorems77.gif)
To compute the derivative, it is convenient to rewrite the function as
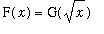
where
| > |
G2 := Int( f2, t=0..x ):
G(x) = G2;
|
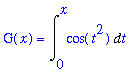
Now, by the Chain Rule,
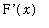 =
=
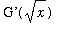
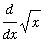
The derivative of G is obtained from the First Fundamental Theorem of Calculus:
`G'`(x) = cos(x^2).
Therefore,
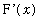 =
=
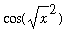
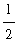
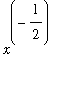
=
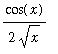 .
.
Notice that this result is consistent with the plot created at the beginning of this example. The function has local extrema at every zero of the cosine function, i.e.,
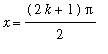 for
for
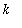 = 0, 1, .... Also, the
= 0, 1, .... Also, the
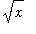 in the denominator of the derivative means that the oscillations decrease as
in the denominator of the derivative means that the oscillations decrease as
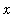 increases.
increases.
To conclude this example, there is a general pattern for differentiating definite integrals when the upper limit is a function. If
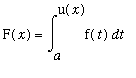
then, by the Chain Rule,
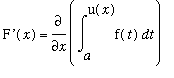
=
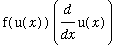
Example 3
Compute
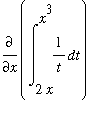
for all values of
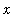 > 0.
> 0.
First, note that
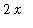 and
and
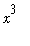 are both positive when
are both positive when
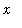 > 0. For 0 <
> 0. For 0 <
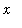 <
<
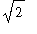 , 0 <
, 0 <
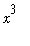 <
<
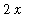 so that the integral will be negative. For
so that the integral will be negative. For
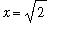 ,
,
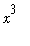 =
=
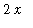 =
=
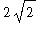 and the integral is zero. For
and the integral is zero. For
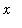 >
>
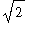 ,
,
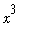 >
>
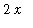 > 0 and the integral is positive.
> 0 and the integral is positive.
| > |
plot( Int( 1/t, t=2*x..x^3 ), x=0..10 );
|
![[Maple Plot]](images/FundamentalTheorems112.gif)
The computation of this derivative is similar to the previous example except that there are functions on both limits of integration. To put this problem in a form where the general result in Example 2 can be used, rewrite the definite integral as
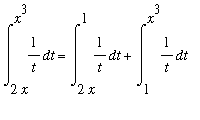
=
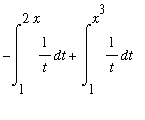 .
.
Now, differentiate using the First Fundamental Theorem of Calculus and the Chain Rule to obtain:

=
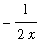
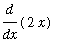 +
+
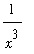
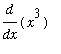
=
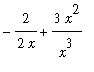
=
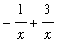
=
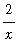 .
.
Remark
Note that
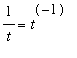 is the one power function for which we do not know an antiderivative. The First Fundamental Theorem of Calculus tells us that an antiderivative for
is the one power function for which we do not know an antiderivative. The First Fundamental Theorem of Calculus tells us that an antiderivative for
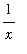 exists (for
exists (for
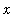 > 0) and can be defined in terms of a definite integral. This topic will be revisited again in the
Evaluating Definite Integrals lesson.
> 0) and can be defined in terms of a definite integral. This topic will be revisited again in the
Evaluating Definite Integrals lesson.
Second Fundamental Theorem of Calculus
Let F be any antiderivative of f on an interval
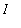 , that is,
, that is,
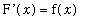 for all
for all
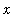 in
in
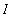 . Then
. Then
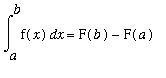 .
.
Proof
Let
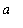 be a number in the interval
be a number in the interval
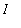 . Define the function G on
. Define the function G on
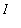 to be
to be
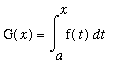 .
.
By the First Fundamental Theorem of Calculus, G is an antiderivative of f. Since F is also an antiderivative of f, it must be that F and G differ by (at most) a constant:
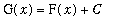
for some value of C. To determine the constant C observe that
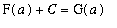
=
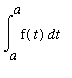 = 0
= 0
and so
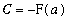 .
.
Therefore,
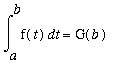
=
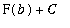
=
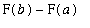 .
.
At last we have an efficient method for evaluating definite integrals:
-
find an antiderivative of the integrand
-
evaluate the antiderivative at the upper limit
-
evaluate the antiderivative at the lower limit
-
subtract the value at the lower limit from the value at the lower limit.
Example 4
The definite integral in Example 1 can now be evaluated as follows:
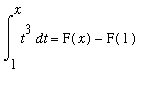
where F is any antiderivative of
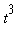 .
.
The simplest antiderivative is
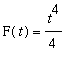 . Thus,
. Thus,
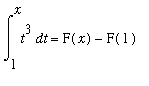
=
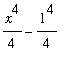
=
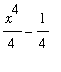 .
.
Note that if F is any other antiderivative of
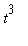 then
then
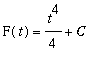 . In this case
. In this case
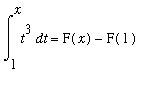
=
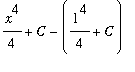
=
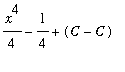
=
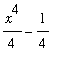 .
.
The important observation to make here is that the same answer is obtained for all antiderivatives of the integrand.
Example 5
Evaluate
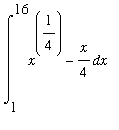 .
.
An antiderivative of
| > |
f5 := x^(1/4) - x/4:
f(x) = f5;
|
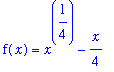
is
| > |
F5 := int( f5, x ):
F(x) = F5;
|
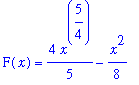
Thus,
| > |
DIval5 := eval( F5, x=16 ) - eval( F5, x=1 ):
Int( f5, x=1..16 ) = F(16)-F(1);
` ` = DIval5;
` ` = simplify( DIval5 );
|
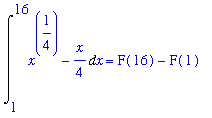
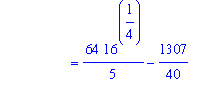
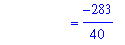
Example 6
Evaluate
| > |
f6 := 3*x + cos(x):
DI6 := Int( f6, x=0..Pi/2 ):
DI6;
|
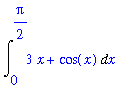
An antiderivative of the integrand is
| > |
F6 := int( f6, x ):
F(x) = F6;
|
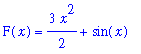
By the Second Fundamental Theorem of Calculus:
| > |
DIval6 := eval( F6, x=Pi/2 ) - eval( F6, x=0 ):
DI6 = F(Pi/2) - F(0);
` ` = DIval6;
` ` = evalf( DIval6 );
|
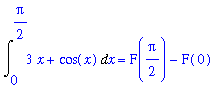
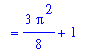
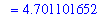
Example 7
Evaluate
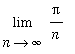
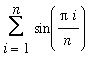 .
.
The form of this limit suggests that it might be the limit of a Riemann sum. Observe that the difference between successive values of
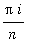 is
is
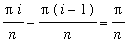 . This suggests that
. This suggests that
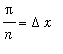 and
and
![Pi*i/n = x[i]](images/FundamentalTheorems170.gif) . With these identifications, the limit now has the form
. With these identifications, the limit now has the form
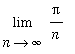
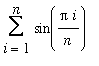 =
=
![Limit(Sum(sin(x[i])*Delta*x,i = 1 .. n),Delta*x = 0)](images/FundamentalTheorems173.gif) .
.
In this form it is apparent that this limit is a (right) Riemann sum for
| > |
f7 := sin(x):
f(x) = f7;
|
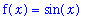
on the interval
| > |
dx := Pi/n:
a7 := 0*dx:
b7 := n*dx:
[ a7, b7 ];
|
![[0, Pi]](images/FundamentalTheorems175.gif)
That is, the limit can be rewritten as a definite integral
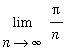
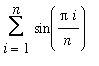 =
=
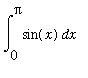 .
.
The value of the definite integral is found uisng the Second Fundamental Theorem of Calculus
| > |
F7 := int( f7, x ):
DI7 := Int( f7, x=a7..b7 ):
DI7 = -'cos'(Pi) - (-'cos'(0));
`` = eval( F7, x=b7 ) - eval( F7, x=a7 );
|
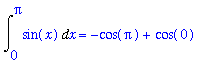
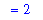
Lesson Summary
The Fundamental Theorems of Calculus are
First Fundamental Theorem of Calculus
Let f be a continuous function on an interval
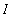 that contains
that contains
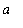 . Define the function F on the interval
. Define the function F on the interval
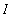 in terms of the definite integral
in terms of the definite integral
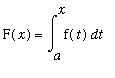 .
.
Then i) F is differentiable on
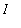 and ii)
and ii)
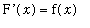 for all
for all
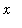 in
in
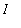 .
.
Second Fundamental Theorem of Calculus
Let F be any antiderivative of f on an interval
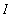 , that is,
, that is,
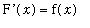 for all
for all
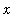 in
in
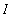 . Then
. Then
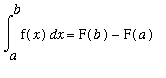 .
.
The First Fundamental Theorem of Calculus is used to define antiderivatives in terms of definite integrals. Alternately, this result provides a new differentiation formula when the limits of integration are functions of the independent variable.
The Second Fundamental Theorem of Calculus provides an efficient method for evaluating definite integrals. All that is needed to be able to use this theorem is any antiderivative of the integrand.
To assist with the determination of antiderivatives, the
Antiderivative
[
Maplet Viewer][
Maplenet] and
Integration
[
Maplet Viewer][
Maplenet] maplets are still available. Of the two, the symbolic capabilities of the
Integration
maplet are most likely to be useful in this lesson.
What's Next?
Now that you have completed this lesson, the
online homework assignment will help develop your skills working with definite integrals. Note there are practice sessions for specific topics, a general practice session for problems related to this lesson, and a graded homework assignment. Work enough practice problems to master these concepts, then complete the online homework assignment and the
assigned problems from the text.
The Fundamental Theorems of Calculus are truly fundamental. If, at the end of this course, you do not know when and how to apply these results, you do not have a good understanding of calculus. The next lesson,
Evaluating Definite Integrals, will help develop your ability to find an antiderivative and how to work with definite integrals. The lessons in
Unit 5 will further develop these skills.
![]() that contains
that contains
![]() . Define the function F on the interval
. Define the function F on the interval
![]() in terms of the definite integral
in terms of the definite integral
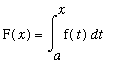 .
.
![]() and ii)
and ii)
![]() for all
for all
![]() in
in
![]() .
.
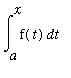 is an antiderivative of f.
is an antiderivative of f.
![]() , that is,
, that is,
![]() for all
for all
![]() in
in
![]() . Then
. Then
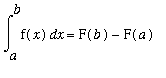 .
.
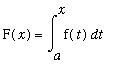 .
.
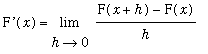
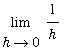 (
(
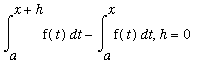 )
)
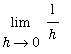 (
(
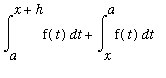 )
)
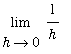
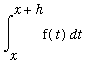
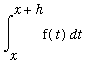 is can be estimated as the "area" of the rectangle with base
is can be estimated as the "area" of the rectangle with base
 is approximately
is approximately
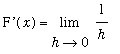
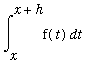
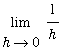 (
(
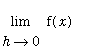
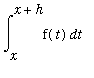 is the average value of f on [
is the average value of f on [
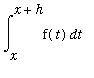 is to use Upper and Lower Riemann sums with 1 subinterval to obtain upper and lower bounds for the integral. Let
is to use Upper and Lower Riemann sums with 1 subinterval to obtain upper and lower bounds for the integral. Let
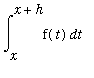 <=
<=
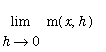 =
=
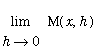 =
=
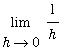
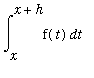 can be completed by an application of the
can be completed by an application of the
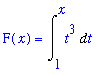
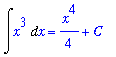
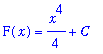
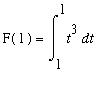 = 0.
= 0.
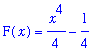
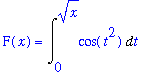
![[Maple Plot]](images/FundamentalTheorems77.gif)
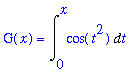
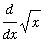
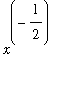
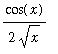 .
.
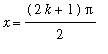 for
for
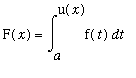
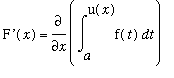
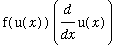
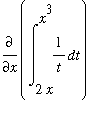
![[Maple Plot]](images/FundamentalTheorems112.gif)
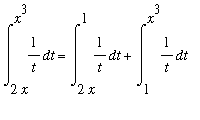
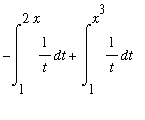 .
.

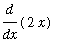 +
+
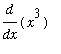
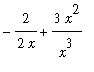
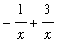
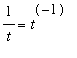 is the one power function for which we do not know an antiderivative. The First Fundamental Theorem of Calculus tells us that an antiderivative for
is the one power function for which we do not know an antiderivative. The First Fundamental Theorem of Calculus tells us that an antiderivative for
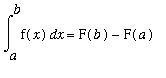 .
.
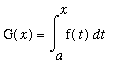 .
.
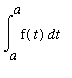 = 0
= 0
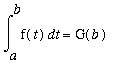
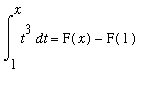
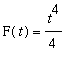 . Thus,
. Thus,
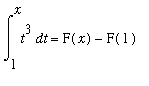
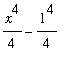
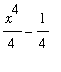 .
.
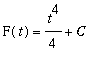 . In this case
. In this case
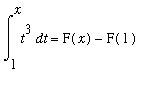
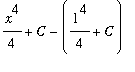
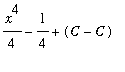
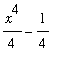 .
.
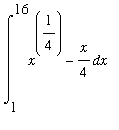 .
.
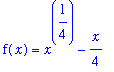
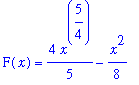
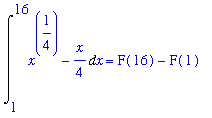
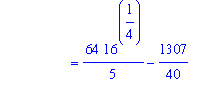
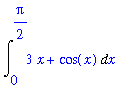
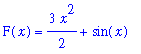
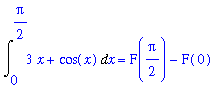
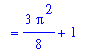
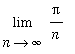
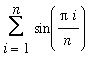 .
.
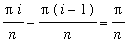 . This suggests that
. This suggests that
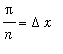 and
and
![Pi*i/n = x[i]](images/FundamentalTheorems170.gif) . With these identifications, the limit now has the form
. With these identifications, the limit now has the form
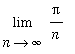
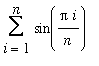 =
=
![Limit(Sum(sin(x[i])*Delta*x,i = 1 .. n),Delta*x = 0)](images/FundamentalTheorems173.gif) .
.
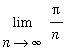
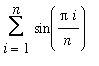 =
=
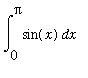 .
.
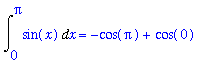
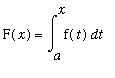 .
.
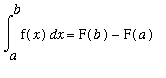 .
.