MeanValueTheorem.mws
Mean Value Theorem
| > |
restart;
with( plots ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Auxiliary Procedures
| > |
InInterval := proc(x,S::list(numeric))
if has(x,I) then return false end if;
return evalb( evalf(x)>=op(1,S) and evalf(x)<=op(2,S) )
end proc:
|
Lesson Overview
The Mean Value Theorem (MVT) is one of the milestones in calculus. The geometric nature of the MVT makes it easy to believe and understand. Some of the more important uses of the MVT are not so geometric and require more effort to understand. In this lesson the MVT will be stated. In place of a proof, examples will be provided to show how the MVT can fail to hold if the hypotheses are not satisfied. Additional examples illustrate some of the results that are based on the MVT. The final example is the foundation for the discussions of
Antiderivatives in the
Unit 4.
The
MeanValueTheorem
maplet [
Maplet Viewer][
MapleNet] provides a nice visualization tool for the basic geometry behind the MVT.
The Mean Value Theorem (MVT)
Recall that the
Intermediate Value Theorem (IVT) states that a continuous function on a closed and bounded interval attains every value between the values at the endpoints at at least one point in the interval. The Mean Value Theorem is similar to the Intermediate Value Theorem except that the MVT says that there is at least one point in the interior of the interval where the first derivative is equal to the slope of the secant line between the endpoints of the interval.
Theorem (Mean Value Theorem)
Let f be a continuous function on [
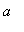 ,
,
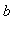 ] with continuous derivative on (
] with continuous derivative on (
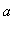 ,
,
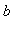 ). Then, there exists at least one number
). Then, there exists at least one number
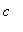 in (
in (
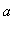 ,
,
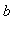 ) for which
) for which
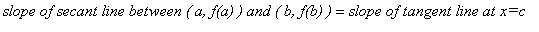
That is,
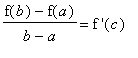 .
.
A visual interpretation of the MVT can be obtained from the
MeanValueTheorem
command in the
Student[Calculus1]
package.
| > |
MeanValueTheorem(x^3 - x, x=-2..2, output = plot);
|
![[Maple Plot]](images/MeanValueTheorem10.gif)
In this example there are two points in the interval ( -2, 2 ) where the slope of the secant line from ( -2, -6 ) to ( 2, 6 ) is parallel to the slope of the tangent line to the graph of
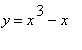 . The secant line is shown as a dashed blue line and the two tangent lines are shown in black.
. The secant line is shown as a dashed blue line and the two tangent lines are shown in black.
Example 1: A Closer Look at the Hypotheses of the MVT
In lieu of a proof of the MVT, this collection of examples illustrates how the MVT can fail to exist when the hypotheses are not satisfied.
Case 1: Hypotheses not satisfied: Function continuous but not differentiable
Consider the function
| > |
f1 := abs(x):
f(x) = f1;
|
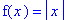
on the interval [ -2, 5 ]
The secant line between ( -2, 2 ) and ( 5, 5 ) has slope
| > |
msec1 := (eval(f1,x=b1)-eval(f1,x=a1))/(b1-a1):
m[secant] = msec1;
|
![m[secant] = 3/7](images/MeanValueTheorem13.gif)
To see that there are no points in this interval where the tangent line to the graph of
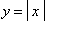 has slope
has slope
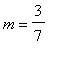 , consider the following plot of
, consider the following plot of
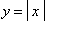 and several lines with slope
and several lines with slope
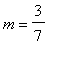 .
.
| > |
plot( [f1, [[-2,2],[5,5]], seq(msec1*x+c,c=-1..3)], x=a1..b1, color=[red,green,blue$5],
title="Visual Proof that MVT does not apply to\nf(x)=abs(x) on [-2,5]" );
|
![[Maple Plot]](images/MeanValueTheorem18.gif)
Algebraically, the derivative of the absolute value function is
| > |
df1 := convert( diff(f1,x), piecewise, x ):
`f '`(x) = df1;
|
![`f '`(x) = PIECEWISE([-1, x < 0],[undefined, x = 0],[1, 0 < x])](images/MeanValueTheorem19.gif)
Because the only values of this derivative are +1 and -1, there are no points where
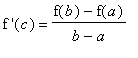 =
=
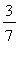 .
.
This is not a contradiction to the MVT because the absolute value function is not differentiable at
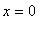 and so is not differentiable on ( -2, 5 ).
and so is not differentiable on ( -2, 5 ).
When Maple's
MeanValueTheorem
encounters this problem, it responds with an appropriate error message
| > |
MeanValueTheorem( f1, a1..b1, output=plot );
|
Error, (in Student:-Calculus1:-MeanValueTheorem) the mean value theorem requires the function to be differentiable on the open interval (a, b)
Case 2: Hypotheses not satisfied: Function not continuous
Consider the function
| > |
f2 := piecewise( x<1, x+1, x>=1, x-1 ):
f(x) = f2;
|
![f(x) = PIECEWISE([x+1, x < 1],[x-1, 1 <= x])](images/MeanValueTheorem23.gif)
on the interval [ 0, 2 ]
The secant line between ( 0, 1 ) and ( 2, 1 ) has slope
| > |
msec2 := (eval(f2,x=b2)-eval(f2,x=a2))/(b2-a2):
m[secant] = msec2;
|
![m[secant] = 0](images/MeanValueTheorem24.gif)
To see that there are no points in this interval where the tangent line to the graph of
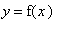 has slope
has slope
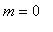 , consider the following plot of
, consider the following plot of
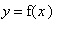 and several lines with slope
and several lines with slope
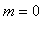 .
.
| > |
plot( [f2, seq(msec2*x+c/2,c=-2..6)], x=a2..b2, color=[red,blue$4,green,blue$4], discont=true,
title="Visual Proof that MVT does not apply to\na function with a discontinuity at x=0 on [-2,5]" );
|
![[Maple Plot]](images/MeanValueTheorem29.gif)
Algebraically, the derivative of this piecewise-defined function is
| > |
df2 := convert( diff(f2,x), piecewise, x ):
`f '`(x) = df2;
|
![`f '`(x) = PIECEWISE([undefined, x = 1],[1, otherwise])](images/MeanValueTheorem30.gif)
Because the only values of this derivative are +1, there are no points where
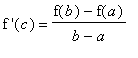 = 0.
= 0.
This is not a contradiction to the MVT because this piecewise defined function is not continuous at
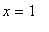 .
.
When Maple's
MeanValueTheorem
encounters this problem, it responds with an appropriate error message
| > |
MeanValueTheorem( f2, a2..b2, output=plot );
|
Error, (in Student:-Calculus1:-MeanValueTheorem) the mean value theorem requires the function to be continuous on the closed interval [a, b]
Case 3: Hypotheses satisfied
Consider the function
| > |
f3 := sin(x)^2:
f(x) = f3;
|
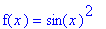
on the interval [ 0,
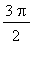 ]
]
The secant line between ( 0, 0 ) and (
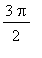 , 1 ) has slope
, 1 ) has slope
| > |
msec3 := (eval(f3,x=b3)-eval(f3,x=a3))/(b3-a3):
m[secant] = msec3;
|
![m[secant] = 2/3/Pi](images/MeanValueTheorem36.gif)
To see that there is at least one point in this interval where the tangent line to the graph of
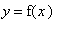 has slope
has slope
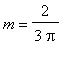 , consider the following plot of
, consider the following plot of
 and several lines with slope
and several lines with slope
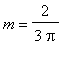 .
.
| > |
plot( [f3, seq(msec3*x+c/8,c=-8..8)], x=a3..b3, color=[red,blue$8,green,blue$8], discont=true,
title="Visual Proof that MVT does apply to\nf(x)=sin(x)^2 on [0,3*Pi/2]" );
|
![[Maple Plot]](images/MeanValueTheorem41.gif)
In this graph there appear to be (at least) two points where a tangent line has the same slope as the secant line. To find these points algebraically, the derivative is
| > |
df3 := diff(f3,x):
`f '`(x) = df3;
|
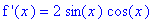
The MVT guarantees there is at least one solution to the equation
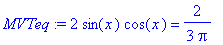
While this transcendental equation is not easily solved by hand, Maple can do the necessary calculations:
| > |
q1 := solve( MVTeq, x ):
q1;
|
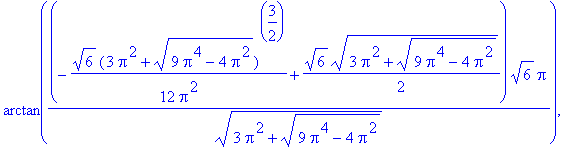
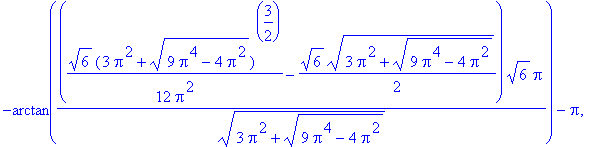
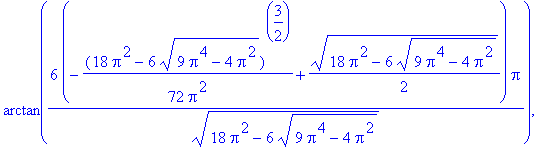
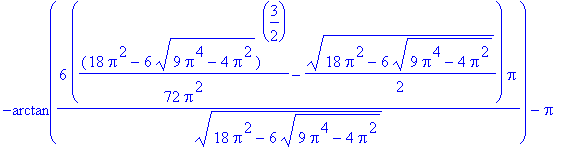
These are the solutions in [
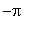 ,
,
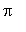 ]; by periodicity, there are four more solutions in [
]; by periodicity, there are four more solutions in [
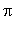 ,
,
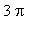 ]. Numerical evaluation of all eight solutions in [
]. Numerical evaluation of all eight solutions in [
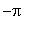 ,
,
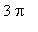 ] are
] are
| > |
q2 := evalf([q1, seq(z+2*Pi,z=q1)]):
q2;
|
![[.1069162122, -3.034676442, 1.463880114, -1.677712540, 6.390101520, 3.248508866, 7.747065422, 4.605472768]](images/MeanValueTheorem54.gif)
and, the values that are in ( 0,
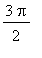 ) are
) are
| > |
MVTc := select( InInterval, q2, [0,evalf(3*Pi/2)] ):
MVTc;
|
![[.1069162122, 1.463880114, 3.248508866, 4.605472768]](images/MeanValueTheorem56.gif)
Thus, there are four values of
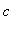 for
for
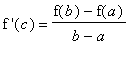 =
=
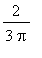 .
.
When Maple's
MeanValueTheorem
encounters this problem, it can return either the graph
| > |
MeanValueTheorem( f3, a3..b3, output=plot );
|
![[Maple Plot]](images/MeanValueTheorem60.gif)
or the explicit values of
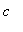 guaranteed by the MVT
guaranteed by the MVT
| > |
q3 := MeanValueTheorem( f3, a3..b3, output=points ):
q3;
|
![[arctan(3/2*Pi-1/2*(9*Pi^2-4)^(1/2)), arctan(3/2*Pi+1/2*(9*Pi^2-4)^(1/2)), arctan(3/2*Pi-1/2*(9*Pi^2-4)^(1/2))+Pi, arctan(3/2*Pi+1/2*(9*Pi^2-4)^(1/2))+Pi]](images/MeanValueTheorem62.gif)
![[.1069162124, 1.463880114, 3.248508866, 4.605472768]](images/MeanValueTheorem63.gif)
Example 2: Using the
MeanValueTheorem
Maplet
To
MeanValueTheorem
maplet [
Maplet Viewer][
MapleNet] is best suited to finding -- visually, symbolically, and numerically -- all points in an interval where the slope of the tangent line equals the slope of the secant line between the endpoints of the interval. To illustrate, let
| > |
f2 := x^2 * sqrt( 5-x ):
f(x) = f2;
|
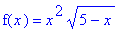
on the interval [ -5, 5 ]. First, note that the domain of this function is (
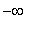 , 5 ]. Moreover, the function is continuous on the closed interval [ -5, 5 ]. The derivative,
, 5 ]. Moreover, the function is continuous on the closed interval [ -5, 5 ]. The derivative,
| > |
df2 := simplify( diff( f2, x ) ):
`f '`(x) = df2;
|
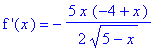
is defined for x in (
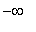 , 5 ); so f is clearly differentiable on the open interval ( -5, 5 ). Thus, the hypotheses of the MVT are satisfied and there will be at least one number
, 5 ); so f is clearly differentiable on the open interval ( -5, 5 ). Thus, the hypotheses of the MVT are satisfied and there will be at least one number
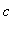 in ( -5, 5 ) for which
in ( -5, 5 ) for which
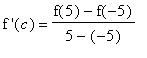 =
=
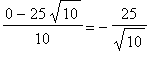 .
.
The algebraic manipulations to solve this equation are rather tedious. In lieu of these calculations, launch the
MeanValueTheorem
maplet [
Maplet Viewer][
MapleNet]. In the top row of the maplet, enter the
Function
(
x^2*sqrt(5-x)
) and endpoints of the interval (
a
=
-5
and
b
=
5
). In the
Display Options
panel, check the
Show function
and
Show secant
boxes, then click the
Plot
button. Observe that the graph of the function has a vertical tangent line at
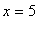 . More relevant to this problem is the observation that there are two locations on the graph of
. More relevant to this problem is the observation that there are two locations on the graph of
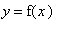 where the tangent line is parallel to the secant line from (
where the tangent line is parallel to the secant line from (
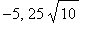 ) to ( 5, 0 ). The maplet finds these points algebraically and symbolically. The algebraic form is rather complicated (you should convince yourself that these roots come from the solution of a fourth-order polynomial); numerically, the two locations are approximately
) to ( 5, 0 ). The maplet finds these points algebraically and symbolically. The algebraic form is rather complicated (you should convince yourself that these roots come from the solution of a fourth-order polynomial); numerically, the two locations are approximately
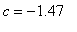 and
and
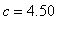 . To have these points identified on the graph, check the
Show points
and
Show tangent line
boxes in the
Display Options
panel, then click the
Plot
button. To terminate the maplet, click the
Close
button.
. To have these points identified on the graph, check the
Show points
and
Show tangent line
boxes in the
Display Options
panel, then click the
Plot
button. To terminate the maplet, click the
Close
button.
Example 3: The MVT and the Highway Patrol
A car travels 203 miles in 3 hours on a highway with speed limit 65mph. Assuming the velocity is continuous for these the entire trip, did the driver ever speed? Did the speed ever exceed the speed limit by at least 10mph?
Solution
Let
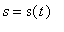 denote the distance traveled (in miles) as a function of time,
denote the distance traveled (in miles) as a function of time,
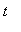 , measured in hours. The velocity is
, measured in hours. The velocity is
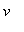 =
=
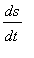 =
=
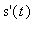 . In terms of the hypotheses of the MVT, the continuity of the velocity means the position,
. In terms of the hypotheses of the MVT, the continuity of the velocity means the position,
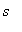 , is differentiable on ( 0, 3 ) and continuous on [ 0, 3 ]. The MVT guarantees the existence of at least one number
, is differentiable on ( 0, 3 ) and continuous on [ 0, 3 ]. The MVT guarantees the existence of at least one number
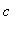 in ( 0, 3 ) where
in ( 0, 3 ) where
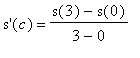 =
=
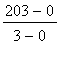 = 67.67 mph.
= 67.67 mph.
That is, there was at least one time --- actually, by continuity of
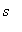 , a time interval contained in ( 0, 3 ) --- when the speed exceeded the speed limit of 65 mph.
, a time interval contained in ( 0, 3 ) --- when the speed exceeded the speed limit of 65 mph.
The MVT has nothing to say about the speed ever exceeding 75mph.
Note
This system is used on toll roads to give speeding tickets at toll booths in some states.]
Example 4: Geometric and Arithmetic Means
Use the MVT to show that
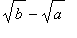 <
<
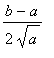 for all 0 <
for all 0 <
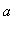 <
<
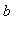 .
.
Then, show that
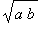 <
<
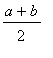 for all
for all
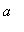 ,
,
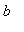 > 0.
> 0.
Solution
Let
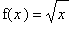 for all
for all
 >= 0. Let
>= 0. Let
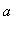 and
and
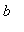 be two positive numbers with
be two positive numbers with
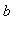 >
>
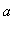 . The function f is continuous on [
. The function f is continuous on [
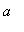 ,
,
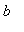 ] and differentiable on (
] and differentiable on (
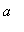 ,
,
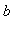 ). (Recall that
). (Recall that
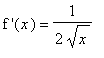 for all
for all
 > 0.) Therefore, the MVT guarantees there is at least one number
> 0.) Therefore, the MVT guarantees there is at least one number
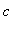 in (
in (
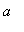 ,
,
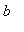 ) with the property
) with the property
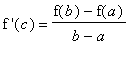 .
.
That is,
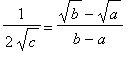 .
.
Now,
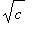 >
>
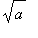 so that
so that
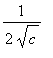 <
<
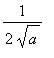 . After multiplication by (the positive quantity) (
. After multiplication by (the positive quantity) (
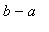 ),
),
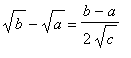 <
<
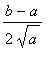 .
.
This completes the proof of the first inequality.
For the second part of this problem, multiply the first inequality by
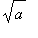 to obtain:
to obtain:
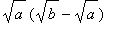 <
<
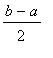
Distributing the multiplication over subtraction yields
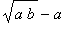 <
<
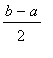
A little more algebra leaves only the radical on the left-hand side of the inequality
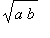 <
<
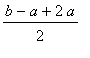
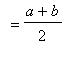 .
.
The importance of this result is that the
geometric mean
of two positive numbers,
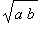 , cannot be larger than the
arithmetic mean
of the same two numbers,
, cannot be larger than the
arithmetic mean
of the same two numbers,
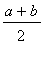 . The geometric and arithmetic means are equal only when
. The geometric and arithmetic means are equal only when
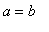 .
.
Example 5: Existence of a Unique Root in an Interval
Show that
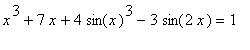 has exactly one real root.
has exactly one real root.
Solution
This problem will be addressed in two steps. First, the MVT will be used to show that there can be at most one solution. Then, the
Intermediate Value Theorem will be used to show that there is at least one solution. Combined, these findings mean there is exactly one solution to this equation.
Define
| > |
f5 := x^3 + 7*x + 4*sin(x)^3 - 3*sin(2*x):
f(x) = f5;
|
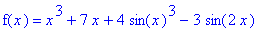
Suppose the equation
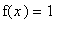 has more than one solution. The goal is to show that this assumption leads to a contradictory conclusion. In this case, the contradition will be that there is a point between
has more than one solution. The goal is to show that this assumption leads to a contradictory conclusion. In this case, the contradition will be that there is a point between
![x[1]](images/MeanValueTheorem132.gif) and
and
![x[2]](images/MeanValueTheorem133.gif) where
where
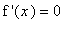 .
.
Let
![x[1]](images/MeanValueTheorem135.gif) and
and
![x[2]](images/MeanValueTheorem136.gif) be two distinct (i.e.,
be two distinct (i.e.,
![x[1] <> x[2]](images/MeanValueTheorem137.gif) ) numbers with
) numbers with
![f(x[1]) = f(x[2])](images/MeanValueTheorem138.gif) = 1. Assume
= 1. Assume
![x[1]](images/MeanValueTheorem139.gif) <
<
![x[2]](images/MeanValueTheorem140.gif) . Note that the function is continuous on [
. Note that the function is continuous on [
![x[1]](images/MeanValueTheorem141.gif) ,
,
![x[2]](images/MeanValueTheorem142.gif) ] and differentiable on (
] and differentiable on (
![x[1]](images/MeanValueTheorem143.gif) ,
,
![x[2]](images/MeanValueTheorem144.gif) ). (In fact, the function is continuous and differentiable for all real numbers.) This means the MVT can be applied. As a result, there must be a number
). (In fact, the function is continuous and differentiable for all real numbers.) This means the MVT can be applied. As a result, there must be a number
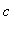 between
between
![x[1]](images/MeanValueTheorem146.gif) and
and
![x[2]](images/MeanValueTheorem147.gif) where
where
![`f '`(c) = (f(x[2])-f(x[1]))/(x[2]-x[1])](images/MeanValueTheorem148.gif) =
=
![(1-1)/(x[2]-x[1])](images/MeanValueTheorem149.gif) = 0.
= 0.
(Note that this conclusion could not be made if
![x[1]](images/MeanValueTheorem150.gif) and
and
![x[2]](images/MeanValueTheorem151.gif) were not assumed to be distinct.)
were not assumed to be distinct.)
Now, lets look at the derivative:
| > |
df5 := diff( f5, x ):
`f '`(x) = df5;
`` = simplify( df5, trig );
|
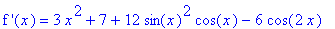
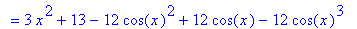
Manual manipulation of this expression continues by writing 13 as 1 + 12, then factoring the trigonometric terms:
`f '`(x) =
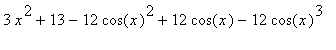
=
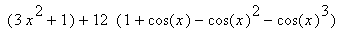
=
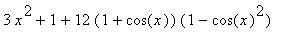
=
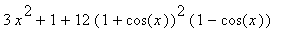
For any value of
 ,
,
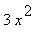 , (
, (
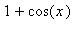 ), and (
), and (
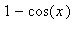 ) are all positive or zero. When combined as in the formula for the derivative, the addition of 1 is sufficient to conclude
) are all positive or zero. When combined as in the formula for the derivative, the addition of 1 is sufficient to conclude
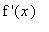 >= 1 for all
>= 1 for all
 . In particular,
. In particular,
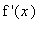 > 0 for all
> 0 for all
 in [
in [
![x[1]](images/MeanValueTheorem166.gif) ,
,
![x[2]](images/MeanValueTheorem167.gif) ].
].
This is a direct contradiction of the result obtained by applying the MVT. Because a true statement cannot lead to two inconsistent results, the hypothesis must be false. There cannot be two distinct solutions. Thus, there is
at most
one real-valued solution to
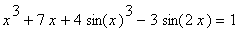 .
.
For the second stage of the problem, the existence of
at least
one solution will be confirmed. It is fairly clear that
| > |
f(0) = eval( f5, x=0 );
|
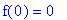
and
| > |
f(Pi) = eval( f5, x=Pi );
|
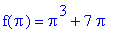
Observe that
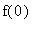 = 0 <1 <
= 0 <1 <
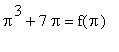
Then, because the function f is continuous on [ 0,
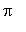 ], the
Intermediate Value Theorem implies that there must be at least one value of
], the
Intermediate Value Theorem implies that there must be at least one value of
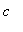 in ( 0,
in ( 0,
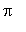 ) for which
) for which
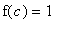 . When combined with the previous result, we have a complete proof that there is exactly one real-valued root of the equation
. When combined with the previous result, we have a complete proof that there is exactly one real-valued root of the equation
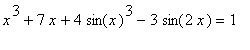 .
.
Moreover, the root occurs somewhere in the interval ( 0,
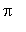 ). A plot of the function, and the line
). A plot of the function, and the line
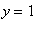 , confirms these results.
, confirms these results.
| > |
plot( [f5,1], x=-2..4 );
|
![[Maple Plot]](images/MeanValueTheorem180.gif)
From this graph it appears the real-value root is near
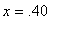 .
.
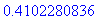
Example 6: Preview of Antiderivatives
Theorem
If
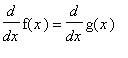 for all
for all
 in an interval, then
in an interval, then
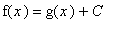 on that interval.
on that interval.
The proof of this theorem involves the Mean Value Theorem. Instead of giving this proof, consider the following illustration of this result.
Consider the functions
| > |
f6a := sin(x)^2:
g6a := -cos(x)^2:
f(x) = f6a;
g(x) = g6a;
|
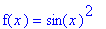
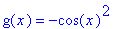
The first derivatives of these functions are
| > |
df6a := diff( f6a, x ):
dg6a := diff( g6a, x ):
`f '`(x) = df6a;
`g '`(x) = dg6a;
|
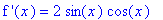
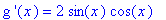
Because these derivatives are equal for all real numbers
 , there must be a constant
, there must be a constant
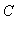 such that
such that
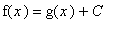 for all real numbers
for all real numbers
 . The constant
. The constant
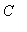 can be determined by selecting any value for
can be determined by selecting any value for
 where it is easy to evaluate
where it is easy to evaluate
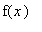 and
and
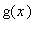 . For example, with
. For example, with
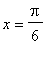 ,
,
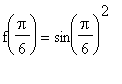 =
=
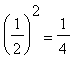
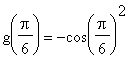 =
=
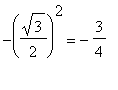
so that
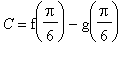 =
=
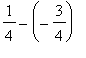 = 1.
= 1.
This is a calculus-based proof of the fundamental trigonometric identity
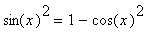 .
.
A graphical display of this result is shown below.
| > |
plot( [f6a,g6a,f6a-g6a], x=-2*Pi..2*Pi, color=[blue,green,red], legend=["y=sin(x)^2", "y=-cos(x)^2", "C=sin(x)^2-cos(x)^2"] );
|
![[Maple Plot]](images/MeanValueTheorem206.gif)
Lesson Summary
The Mean Value Theorem (MVT) makes sense intuitively. (If you do not agree with this statement, it is likely that you do not understand the geometry of the MVT. Please review this lesson and your textbook; get outside assistance if needed.) Example 1 illustrates why the function is required to be continuous on a closed interval and differentiable on the same interval, except possibly at the endpoints. Finding the location where the tangent line to the graph is parallel to the secant line connecting the endpoints of the graph on the given interval, as in Example 2, is best done with the aid of the MeanValueTheorem maplet [
Maplet Viewer][
MapleNet]. The more interesting applications of the MVT (Examples 3 - 5) use the MVT without finding the location of the points guaranteed by the MVT.
The final example, Example 6, provides a first look at antiderivatives. This will be discussed in greater detail in the
Antiderivatives lesson in
Unit 4.
What's Next?
This concludes the unit on applications of derivatives. While there are many more applications of derivatives, the ones presented in this unit provide a foundation from which you should be able to understand most other applications.
As usual, there is a collection of online practice problems associated with this lesson. Complete these problems first, then complete the
online homework assignment. Then, complete the
textbook homework assignment.
As this concludes this unit, there is an online quiz.
Quiz 6 contains questions pertaining to the
Graphing,
Optimzation, and Mean Value Theorem lessons.
To conclude, review the material in the
Graphing and
Optimization lessons (as well as this lesson) before taking the quiz on the second half of this unit.
![]() ,
,
![]() ] with continuous derivative on (
] with continuous derivative on (
![]() ,
,
![]() ). Then, there exists at least one number
). Then, there exists at least one number
![]() in (
in (
![]() ,
,
![]() ) for which
) for which
![]()
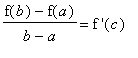 .
.
![[Maple Plot]](images/MeanValueTheorem10.gif)
 . The secant line is shown as a dashed blue line and the two tangent lines are shown in black.
. The secant line is shown as a dashed blue line and the two tangent lines are shown in black.
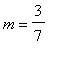 , consider the following plot of
, consider the following plot of
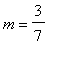 .
.
![[Maple Plot]](images/MeanValueTheorem18.gif)
![`f '`(x) = PIECEWISE([-1, x < 0],[undefined, x = 0],[1, 0 < x])](images/MeanValueTheorem19.gif)
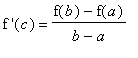 =
=
![f(x) = PIECEWISE([x+1, x < 1],[x-1, 1 <= x])](images/MeanValueTheorem23.gif)
![[Maple Plot]](images/MeanValueTheorem29.gif)
![`f '`(x) = PIECEWISE([undefined, x = 1],[1, otherwise])](images/MeanValueTheorem30.gif)
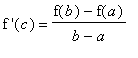 = 0.
= 0.
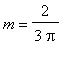 , consider the following plot of
, consider the following plot of
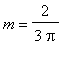 .
.
![[Maple Plot]](images/MeanValueTheorem41.gif)
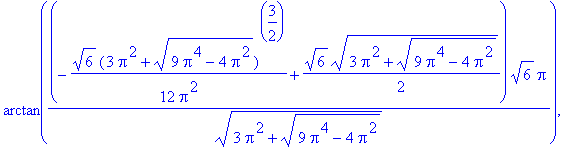
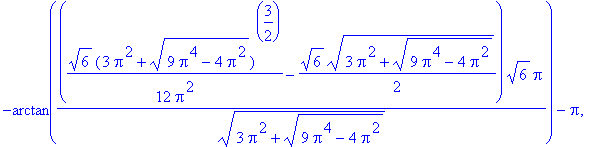
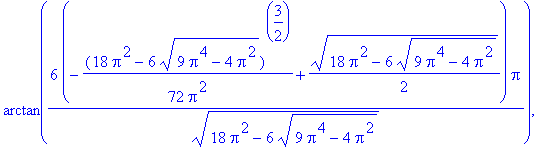
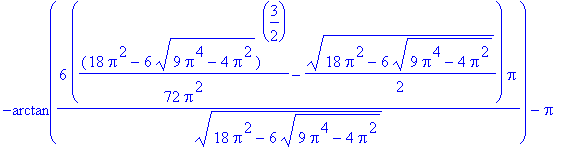
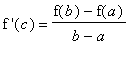 =
=
![[Maple Plot]](images/MeanValueTheorem60.gif)
![[arctan(3/2*Pi-1/2*(9*Pi^2-4)^(1/2)), arctan(3/2*Pi+1/2*(9*Pi^2-4)^(1/2)), arctan(3/2*Pi-1/2*(9*Pi^2-4)^(1/2))+Pi, arctan(3/2*Pi+1/2*(9*Pi^2-4)^(1/2))+Pi]](images/MeanValueTheorem62.gif)
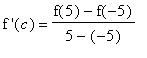 =
=
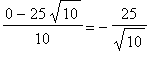 .
.
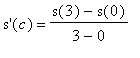 =
=
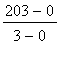 = 67.67 mph.
= 67.67 mph.
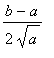 for all 0 <
for all 0 <
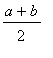 for all
for all
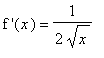 for all
for all
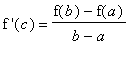 .
.
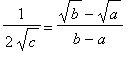 .
.
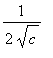 <
<
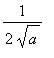 . After multiplication by (the positive quantity) (
. After multiplication by (the positive quantity) (
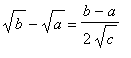 <
<
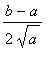 .
.
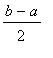
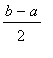
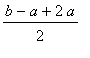
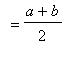 .
.
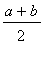 . The geometric and arithmetic means are equal only when
. The geometric and arithmetic means are equal only when
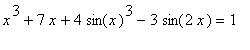 has exactly one real root.
has exactly one real root.
![`f '`(c) = (f(x[2])-f(x[1]))/(x[2]-x[1])](images/MeanValueTheorem148.gif) =
=
![(1-1)/(x[2]-x[1])](images/MeanValueTheorem149.gif) = 0.
= 0.
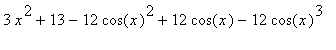
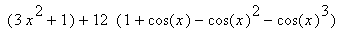
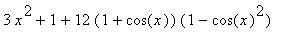
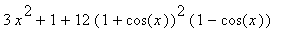
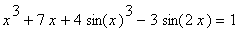 .
.
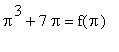
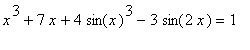 .
.
![[Maple Plot]](images/MeanValueTheorem180.gif)
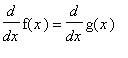 for all
for all
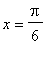 ,
,
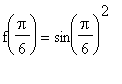 =
=
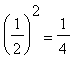
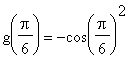 =
=
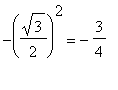
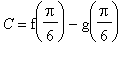 =
=
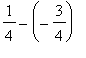 = 1.
= 1.
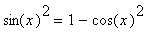 .
.
![[Maple Plot]](images/MeanValueTheorem206.gif)