Example 1 - Bisection Method
Consider the function
| > |
f := x -> (x^5 - 4*x^2 + 2)/(x-1):
`f(x)` = f(x);
|
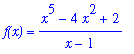
A plot of this function suggests that there are three real solutions to
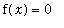 .
.
| > |
plot( f(x), x=-5..5, y=-10..10, discont=true );
|
![[Maple Plot]](images/LimitIntermediateValue11.gif)
It appears as though one of the solutions to
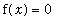 is in the closed interval [-1,0]. The IVT confirms this as the function f is continuous on [-1,0] and
is in the closed interval [-1,0]. The IVT confirms this as the function f is continuous on [-1,0] and
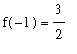 >0 and
>0 and
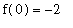 < 0.
< 0.
The Bisection Method carries this idea further.
Step 1:
The midpoint of
![[-1, 0]](images/LimitIntermediateValue15.gif) is
is
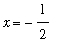 ; because
; because
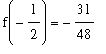 <0 the IVT tells us the solution will be found in
<0 the IVT tells us the solution will be found in
![[-1, -1/2]](images/LimitIntermediateValue18.gif) .
.
Step 2:
The midpoint of
![[-1, -1/2]](images/LimitIntermediateValue19.gif) is
is
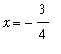 ; because
; because
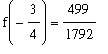 >0 the IVT tells us the solution will be found in
>0 the IVT tells us the solution will be found in
![[-3/4, -1/2]](images/LimitIntermediateValue22.gif) .
.
This process can be continued until the interval is sufficiently short. To implement this in Maple, let
max_len
denote the length of the interval when the iteration should stop.
| > |
bisect := proc( f::procedure, II::range, max_len::positive )
local a, b, c;
a := op(1,II);
b := op(2,II);
if signum(f(a))=signum(f(b)) or not iscont(f(x),x=II) then
error "the IVT does not apply on the interval", II
end if;
while abs(b-a)>max_len do
c := (a+b)/2;
if f(c)=0 then
break
elif signum(f(a))=signum(f(c)) then
a := c
else
b := c
end if;
end do:
return( [a..b] )
end proc:
|
When the Bisection Method is restarted on [-1,0] with a tolerance of
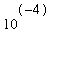 = 0.0001:
= 0.0001:
| > |
bisect( f, -1...0., 10^(-4) );
|
![[-.6807861327 .. -.6807250976]](images/LimitIntermediateValue24.gif)
The conclusion that this root occurs on [-0.680786, -0.680725] is consistent with the result from Maple's
fsolve
command:

The other real roots of this function can be approximated in the same way. Note that the IVT
cannot
be applied on
![[0, 1]](images/LimitIntermediateValue26.gif) ,
,
![[1, 2]](images/LimitIntermediateValue27.gif) , or any interval containing
, or any interval containing
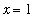 because the function has a vertical asymptote at
because the function has a vertical asymptote at
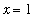 (and so cannot be continuous there). It is not difficult, however, to avoid this difficulty because we know
(and so cannot be continuous there). It is not difficult, however, to avoid this difficulty because we know
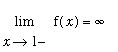 and
and
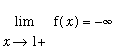 . For the smaller positive root we can apply the Bisection Method on [0,0.99]:
. For the smaller positive root we can apply the Bisection Method on [0,0.99]:
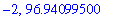
| > |
bisect( f, 0..0.99, 10^(-4) );
|
![[.7470922852 .. .7471527100]](images/LimitIntermediateValue33.gif)
| > |
fsolve( f(x)=0, x, x=0..0.99 );
|
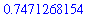
Again the result is consistent with Maple's approximation to this solution:
The second positive root can be found by applying the Bisection Method on [1.01,2]:

| > |
bisect( f, 1.01..2, 10^(-4) );
|
![[1.450013428 .. 1.450073852]](images/LimitIntermediateValue36.gif)
| > |
fsolve( f(x)=0, x , x=1.01..2 );
|
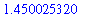
Example 2 - Periodic Temperatures
Suppose the temperature at midnight is 55 degrees, increases to a high of 85 degrees, then returns to 55 degrees at midnight the next day. Assume that the temperature throughout the day is a continuous function of the time of day.
Use the IVT to show that there is at least one time in the morning when the temperature is the same as the temperature exactly 12 hours later.
Let
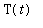 denote the temperature (in degrees) at time
denote the temperature (in degrees) at time
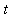 for 0 <=
for 0 <=
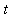 <= 24. Define the function f by
<= 24. Define the function f by
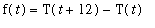 for 0 <=
for 0 <=
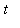 <= 12. Then
<= 12. Then
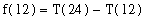 =
=
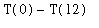 =
=
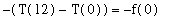 .
.
Case 1:
If
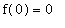 then the
then the
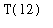 =
=
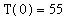 and we have two times 12 hours apart when the temperatures are equal.
and we have two times 12 hours apart when the temperatures are equal.
Case 2:
If
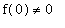 , then
, then
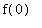 and
and
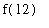 have different signs. Because T is continuous throughout the day, f must be continuous on [0,12]. The IVT can be applied to conclude that there is at least one time
have different signs. Because T is continuous throughout the day, f must be continuous on [0,12]. The IVT can be applied to conclude that there is at least one time
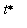 in (0,12) when
in (0,12) when
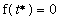 ; that is,
; that is,
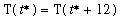 .
.
Since exactly one of these two cases must be true, the proof is complete. [Note that the information about the high temperature is unneeded.]
![]() and let
and let
![]() be a number between
be a number between
![]() and
and
![]() . The equation
. The equation
![]() has at least one solution
has at least one solution
![]() in the open interval (
in the open interval (
![]() ,
,
![]() ).
).
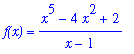
![[Maple Plot]](images/LimitIntermediateValue11.gif)
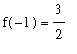 >0 and
>0 and
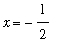 ; because
; because
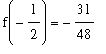 <0 the IVT tells us the solution will be found in
<0 the IVT tells us the solution will be found in
![[-1, -1/2]](images/LimitIntermediateValue18.gif) .
.
![[-1, -1/2]](images/LimitIntermediateValue19.gif) is
is
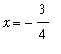 ; because
; because
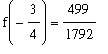 >0 the IVT tells us the solution will be found in
>0 the IVT tells us the solution will be found in
![[-3/4, -1/2]](images/LimitIntermediateValue22.gif) .
.
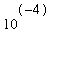 = 0.0001:
= 0.0001:
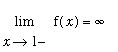 and
and
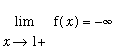 . For the smaller positive root we can apply the Bisection Method on [0,0.99]:
. For the smaller positive root we can apply the Bisection Method on [0,0.99]: