LimitInfinite.mws
Infinite Limits
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
This lesson continues some of the discussions begun in the
Limits at Infinity lesson. The first goal is to complete our knowledge about limits at infinity for all power functions. With this information it will be possible to evaluate all limits at infinity (or negative infinity) of rational polynomials -- including those in which the degree of the numerator is larger than the degree of the denominator. Functions that are not defined at points because of problems with division by zero are considered next. Because these limit points are finite, it is necessary to consider both two-sided and one-sided limits. The lesson concludes with the definition of vertical and oblique asymptotes.
The underlying theme for each of these discussions is an infinite limit:
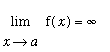 . That is, for values of
. That is, for values of
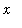 near
near
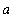 , all of the function values must be increasing without bound. For one-sided limits values of
, all of the function values must be increasing without bound. For one-sided limits values of
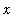 are chosen from only one side of the the limit point. In many ways limits at infinity are the easiest to understand; that is where the discussion begins.
are chosen from only one side of the the limit point. In many ways limits at infinity are the easiest to understand; that is where the discussion begins.
Limits at Infinity for Powers
Reciprocal powers were considered in the
Limits at Infinity lesson. To complete that discussion it is necessary to consider the limits
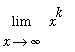 with
with
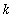 > 0.
> 0.
It seems almost obvious that we should expect
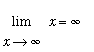 . Think about what this limit means: as the values of the independent varaiable increase without bound, the function values also increase without bound. Since the function is the identity function, its values are the same as the independent variable. With this result the Identity Law for limits (see the
Limit Laws lesson) is now extended to cases when the limit point is a real number,
. Think about what this limit means: as the values of the independent varaiable increase without bound, the function values also increase without bound. Since the function is the identity function, its values are the same as the independent variable. With this result the Identity Law for limits (see the
Limit Laws lesson) is now extended to cases when the limit point is a real number,
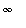 , or
, or
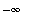 .
.
In a similar way, the other limit laws can be extended to limits at infinity. While this process is generally straightforward, special care must be recognize when the resulting operation is not defined. For example, the Difference Law does not apply when both functions have infinite limits because
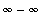 is undefined. Other problematic situations include
is undefined. Other problematic situations include
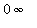 and
and
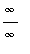 . When these indeterminate forms arise, they are handled very much the same way that
. When these indeterminate forms arise, they are handled very much the same way that
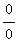 cases were handled in the
Conceptual Understanding of Limits lesson.
cases were handled in the
Conceptual Understanding of Limits lesson.
In addition to this extension of the
Limit Laws to limits at infinity, our understanding of limits at infinity for all (rational) powers can be summarized as
![limit(x^k,x = infinity) = PIECEWISE([infinity, `k > 0`],[1, `k = 0`],[0, `k < 0`])](images/LimitInfinite14.gif)
A visual representation of these results can be seen in the following plot
| > |
K := [ -3, -2, -4/3, -1, -1/2, 0, 1/2, 1, 4/3, 2, 3]:
F_list := [seq( convert(x^k,surd), k=K )]:
L_list := [seq( sprintf("k=%a",k), k=K )]:
C_list := [red,green,pink,cyan,blue,magenta,blue,cyan,pink,green,red]:
plot( F_list, x=1..5, y=0..20,
title="Plots of y=x^k for large positive values of x",
legend=L_list, color=C_list );
|
![[Maple Plot]](images/LimitInfinite15.gif)
The corresponding limits at negative infinity are
![limit(x^k,x = -infinity) = PIECEWISE([infinity, `k = p/q > 0 with p even and q odd`],[-infinity, `k=p/q > 0 with p and q both odd`],[1, `k = 0`],[0, `k = p/q < 0 with q odd`],[`d.n.e.`, `k=p/q with q e...](images/LimitInfinite16.gif)
The two plots that follow are created by the same Maple commands except that the domain (and range) are changed to reflect the behavior for positive and negative values of
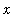 .
.
A graphical summary of this result is provided in the following plot.
| > |
P2 := plot( F_list, x=-5..-1, y=-10..10, legend=L_list, color=C_list,
title="Plots of y=x^k for large negative values of x" ):
P2;
|
![[Maple Plot]](images/LimitInfinite18.gif)
The fact that the plot commands to created the plots for positive and for negative values of x differ only in the domain and range. But, notice that the curves for
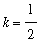 and
and
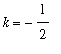 do not appear in the plot for
do not appear in the plot for
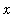 < 0. This is consistent with the summary of the limits at negative infinity because the square root function (and any other even root) is not defined for negative numbers.
< 0. This is consistent with the summary of the limits at negative infinity because the square root function (and any other even root) is not defined for negative numbers.
Example 1 - Rational Function
A new class of problems that we can evaluate is limits at infinity of a rational function in which the numerator has a higher degree than the denominator
| > |
f1 := (31*x^6-26*x^5-62*x^4+x^3-47*x-91)/(-47*x^5-61*x^4+41*x^3-58*x^2-90*x+53):
n1 := numer( f1 ):
d1 := denom( f1 ):
L1 := Limit( f1, x=infinity ):
L1;
|
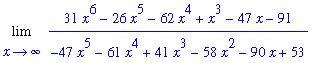
The leading degree in the denominator is
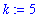
Dividing both numerator and denominator by
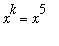 produces the equivalent problem
produces the equivalent problem
| > |
n2 := expand( n1/x^k ):
d2 := expand( d1/x^k ):
f2 := n2/d2:
L2 := Limit( f2, x=infinity ):
L1 = L2;
|
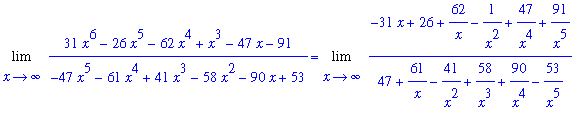
Note that the limit of the denominator exists and is non-zero:
| > |
d3 := Limit( d2, x=infinity ):
d3 = value(d3);
|
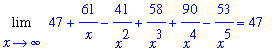
Note that the limit of the numerator is infinity. The (extended) Quotient Rule for limits can be applied to determine the value for this limit
| > |
L3 := Limit( n2, x=infinity ) / d3:
L2 = L3;
`` = value( L3 );
|
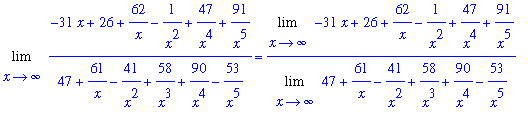
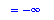
The limit as
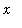 decreases without bound can be found in exactly the same manner:
decreases without bound can be found in exactly the same manner:
| > |
L4 := Limit( f1, x=-infinity ):
L5 := Limit( n2, x=-infinity ) / Limit( d2, x=-infinity ):
L4 = L5;
`` = value( L5 );
|
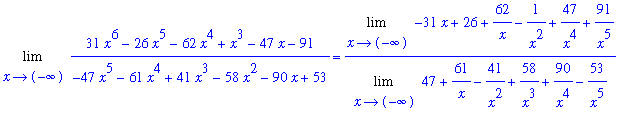
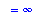
A plot of this function confirms that these results are reasonable.
| > |
p1 := plot( f1, x=1..10 ):
p2 := plot( f1, x=-10..-2 ):
display( [p1,p2] );
|
![[Maple Plot]](images/LimitInfinite32.gif)
As before, simply looking at this plot is insufficient. Knowledge about the function's behavior for -10 <
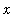 < -2 and 1 <
< -2 and 1 <
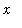 < 10 does not predict anything about its behavior for
< 10 does not predict anything about its behavior for
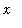 < -10 or
< -10 or
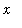 > 10. The plot is, however, a useful tool when used in combination with the preceding analysis. The analysis of this function will continue in Examples 2 and 4 later in this lesson.
> 10. The plot is, however, a useful tool when used in combination with the preceding analysis. The analysis of this function will continue in Examples 2 and 4 later in this lesson.
Limits at the Origin for Powers
An observant reader will realize that the plots that there are two plots immediately before Example 1 because something completely different happens near the origin,
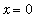 . Here the situation is the complement of the analysis just completed for limits at infinity. The Power Law for limits tell us that
. Here the situation is the complement of the analysis just completed for limits at infinity. The Power Law for limits tell us that
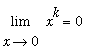 whenever
whenever
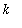 is a positive integer or a rational number with an odd denominator. (If the denominator is even, then
is a positive integer or a rational number with an odd denominator. (If the denominator is even, then
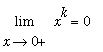 but the two-sided limit does not exist.) What happens to negative powers of x near the origin?
but the two-sided limit does not exist.) What happens to negative powers of x near the origin?
The simplest example to consider is
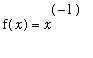 =
=
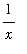 for
for
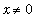 . If
. If
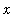 is a small positive number, then
is a small positive number, then
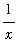 is a large positive number and the right-hand limit should be infinity:
is a large positive number and the right-hand limit should be infinity:
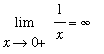
If
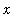 is a small negative number, then
is a small negative number, then
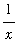 will be a large negative number. This suggests the left-hand limit should be
will be a large negative number. This suggests the left-hand limit should be
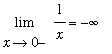
Thus, the two-sided limit
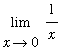 does not exist.
does not exist.
Consider now
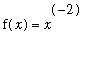 =
=
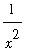 for
for
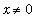 . Because
. Because
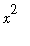 is positive for all
is positive for all
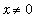 ,
,
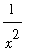 is a large positive number when
is a large positive number when
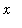 is small -- either positive or negative. Therefore,
is small -- either positive or negative. Therefore,
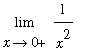 =
=
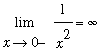 and so the corresponding two-sided limit does exist
and so the corresponding two-sided limit does exist
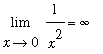 .
.
In general, these limits can be summarized with the following two statements:
![limit(x^k,x = 0,right) = PIECEWISE([0, `k > 0`],[1, `k = 0`],[infinity, `k < 0`])](images/LimitInfinite61.gif)
![limit(x^k,x = 0,left) = PIECEWISE([0, `k = p/q > 0 with q odd`],[1, `k = 0`],[-infinity, `k = p/q < 0 with p and q both odd`],[infinity, `k = p/q < 0 with p even and q odd`],[`d.n.e.`, `k = p/q with q ...](images/LimitInfinite62.gif)
There is no reason to create the corresponding summary for two-sided limits. The two sided limit exists only if both one-sided limits exist and are equal.
| > |
P3 := plot( F_list, x=-2..2, y=-10..10, legend=L_list, color=C_list,
title="Plots of y=x^k for small values of x" ):
P3;
|
![[Maple Plot]](images/LimitInfinite63.gif)
To conclude this discussion, observe that there is a very strong connection between these one-sided limits for powers at zero and the limits for powers at infinity and negative infinity.
Vertical Asymptotes
In the previous section of this lesson we considered only simple powers and limits at the origin.
Recall that the Quotient Rule for Limits can be applied only when the limit of the denominator exists and is not zero. If the limits of the numerator and denominator are both zero, there is a chance that additional manipulation of the function can produce an equivalent formulation of the problem that avoids division by zero. If the limit of the numerator is not zero then we need to consider one-sided limits and be alert to the possibility that one or more of these limits could be infinite.
Definition - Vertical Asymptote
A
vertical asymptote
to the graph of
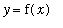 is a (vertical) line
is a (vertical) line
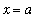 where at least one of the one-sided limits of
where at least one of the one-sided limits of
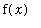 at
at
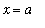 is
is
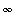 or
or
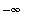 .
.
For example, the graph of
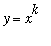 for any
for any
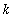 < 0 has a vertical asymptote at
< 0 has a vertical asymptote at
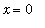 .
.
Note that a function can have more than one vertical asymptote. At each vertical asymptote the graph of a function will jump. (The function could jump at other points as well; this will be discussed in more detail in the
Continuity lesson.)
Example 2 - Rational Function (cont.)
The function
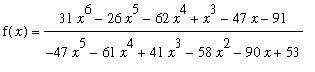
was first encountered in Example 1. At that time it was determined that
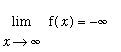 and
and
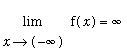 . These analytic results were supported by a plot of the function for -10 <
. These analytic results were supported by a plot of the function for -10 <
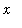 < -2 and 1 <
< -2 and 1 <
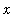 < 10.
< 10.
The purpose of this example is to determine any and all vertical asymptotes for this function. Based on the plot produced in Example 1, all vertical asymptotes must occur in the interval -2 < x < 1. Maple can create a very nice plot of this function
| > |
p3 := plot( f1, x=-2..1, y=-10..20, color=blue, discont=true ):
display( [p1,p2,p3] );
|
![[Maple Plot]](images/LimitInfinite78.gif)
Based on this picture there appear to be three vertical asymptotes. To accurately locate these vertical lines we begin by locating the (real) zeroes of the denominator. Because the denominator is a quintic polynomial with real coefficients it must have five zeroes - including possibly one or two pairs of complex conjugates. It is not possible to find an explicit representation for these roots. Approximations to the real roots of the polynomial are found with the use of the
fsolve
command:
| > |
Zf_r := fsolve( denom(f1)=0, x );
|
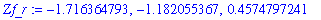
The left- and right-hand limits for each of these approximate roots are reported in the following loop:
| > |
for a in Zf_r do
LL := Limit( f1, x=a, left ):
LR := Limit( f1, x=a, right ):
print( LL = value( LL ), LR = value( LR ) );
end do:
|
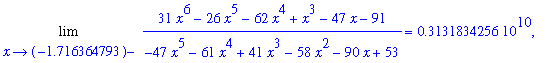
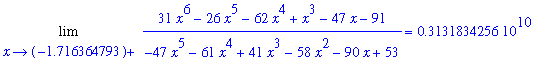
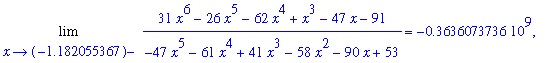
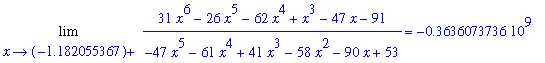
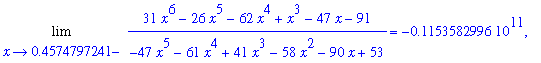
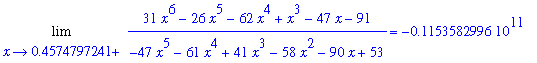
While none of these limits is infinite, all values are extremely large. The reason for this is that the roots are only approximate. The large values are strong indications that each of these values is an approximation to a vertical asymptote of the function. Additional support for these values being vertical asymptotes is obtained in the following plot.
| > |
p4 := implicitplot( {seq(x=a,a=Zf_r)}, x=-2..1, y=-10..20, color=cyan ):
display( [p1,p2,p3,p4], title="Plot of function and vertical asymptotes" );
|
![[Maple Plot]](images/LimitInfinite86.gif)
Example 3 - Trigonometric Function
Vertical asymptotes are found in trigonometric functions whenever a zero is encountered in the denominator. The most common example is the tangent function
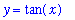
The tangent function is defined for all values of x for which
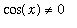 . In general,
. In general,
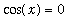 when
when
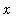 is an odd multiples of
is an odd multiples of
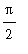 . For example,
. For example,
| > |
Z := [ seq( (2*k+1)*Pi/2, k=($-3..3) ) ];
|
![Z := [-5/2*Pi, -3/2*Pi, -1/2*Pi, 1/2*Pi, 3/2*Pi, 5/2*Pi, 7/2*Pi]](images/LimitInfinite92.gif)
| > |
t1 := plot( g, x=-3*Pi..4*Pi, y=-20..20, discont=true ):
t2 := implicitplot( {seq(x=a,a=Z)}, x=-8..12, y=-20..20, color=cyan ):
display( [t1,t2], title="Plot of function and vertical asymptotes" );
|
![[Maple Plot]](images/LimitInfinite93.gif)
Oblique Asymptotes
When the graph of a function,
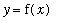 , approaches a horizontal line,
, approaches a horizontal line,
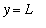 , as
, as
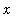 increases or decreases without bound, the line
increases or decreases without bound, the line
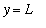 is a horizontal asymptote of
is a horizontal asymptote of
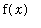 . A rational function has a horizontal asymptote when the numerator and denominator both have the same degree. An oblique asymptote is similar; the difference is that the line the graph of
. A rational function has a horizontal asymptote when the numerator and denominator both have the same degree. An oblique asymptote is similar; the difference is that the line the graph of
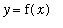 approaches can have a non-zero slope.
approaches can have a non-zero slope.
Definition - Oblique Asymptote
An
oblique asymptote
to the graph of
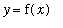 is a line
is a line
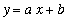 where
where
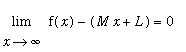 or
or
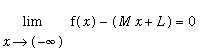 .
.
A rational function has an oblique asymptote only when the degree of the numerator is one more than the degree of the denominator. Long (or synthetic) division can be used to find the equation of the oblique asymptote. (You can stop as soon as you have a remainder whose degree is smaller than the degree of the denominator.)
Example 4 - Rational Function (cont.)
To conclude the investigation of the function considered in Examples 1 and 2, find its oblique asymptote. In this case, long division yields
| > |
q1 := series( f1, x=infinity, 1 ):
f1 = q1;
|
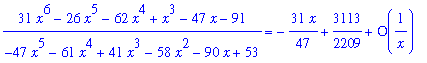
so that the oblique asymptote is
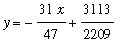 .
.
Adding the graph of the oblique asymptote to the previous graph completes our analysis of this function.
| > |
OA := convert( q1, polynom ):
p5 := plot( OA, x=-10..10, discont=true, color=green ):
display( [p1,p2,p3,p4,p5], title="Plot of function with vertical and oblique asymptotes" );
|
![[Maple Plot]](images/LimitInfinite106.gif)
Note that it is not a concern that the graph of
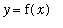 crosses an oblique asymptote. The same would be true if the function had a horizontal asymptote. But, the graph of a function
crosses an oblique asymptote. The same would be true if the function had a horizontal asymptote. But, the graph of a function
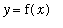 will never intersect a vertical asymptote.
will never intersect a vertical asymptote.
Example 5 - A Function with All Three Types of Asymptotes
In general, difficult - ex w/ large root; Maple's infinity plot can be helpful but not the answer for everything.
To conclude our discussion of limits at infinity and infinite limits, consider the function
| > |
f := ( x^3 + abs(x)^3 - 6*x^2 + 12 ) / ( x+2 )^2:
`f(x)`=f;
|
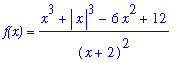
Our objective is to determine all asymptotes (vertical, horizontal, and oblique) for this function and to prepare a plot of the function and all of its asymptotes.
A plot of the function is not difficult to obtain.
| > |
pf := plot( f, x=-10..20, y=-100..30, discont=true ):
pf;
|
![[Maple Plot]](images/LimitInfinite110.gif)
An important observation is that for x > 0 and for x < 0 the function simplifies to
different
rational functions.
| > |
f_pos := simplify( f ) assuming x::positive:
f_neg := simplify( f ) assuming x::negative:
f = piecewise( x>0, f_pos, x<0, f_neg );
|
![(x^3+abs(x)^3-6*x^2+12)/(x+2)^2 = PIECEWISE([2*(x^3-3*x^2+6)/(x+2)^2, 0 < x],[-6*(x^2-2)/(x+2)^2, x < 0])](images/LimitInfinite111.gif)
This means the function should be expected to have different asymptotic behavior at infinity and negative infinity. For x > 0, the rational function has an oblique asymptote
| > |
q2 := series( f_pos, x=infinity, 4 ):
OA_f := y = convert( q2, polynom ):
OA_f;
|
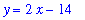
For x<0, the rational function has a horizontal asymptote
| > |
HA_f := y = limit( f, x=-infinity ):
HA_f;
|
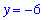
To find any vertical asymptotes, the zeroes of the denominator are easily seen to be
| > |
VA_f := seq( x=a, a={solve( denom(f)=0, x )} ):
VA_f;
|
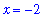
| > |
pa := implicitplot( {OA_f,HA_f,VA_f}, x=-10..20, y=-100..30, color=cyan ):
display( [pf,pa], title="Plot of function and all asymptotes" );
|
![[Maple Plot]](images/LimitInfinite115.gif)
Lesson Summary
The limits of simple powers at the origin and at both infinities are summarized in the following four results
![limit(x^k,x = infinity) = PIECEWISE([infinity, `k > 0`],[1, `k = 0`],[0, `k < 0`])](images/LimitInfinite116.gif)
![limit(x^k,x = -infinity) = PIECEWISE([infinity, `k = p/q > 0 with p even and q odd`],[-infinity, `k=p/q > 0 with p and q both odd`],[1, `k = 0`],[0, `k = p/q < 0 with q odd`],[`d.n.e.`, `k=p/q with q e...](images/LimitInfinite117.gif)
![limit(x^k,x = 0,right) = PIECEWISE([0, `k > 0`],[1, `k = 0`],[infinity, `k < 0`])](images/LimitInfinite118.gif)
![limit(x^k,x = 0,left) = PIECEWISE([0, `k = p/q > 0 with q odd`],[1, `k = 0`],[-infinity, `k = p/q < 0 with p and q both odd`],[infinity, `k = p/q < 0 with p even and q odd`],[`d.n.e.`, `k = p/q with q ...](images/LimitInfinite119.gif)
Notice how the limit at infinity is related to the limit at the origin from the right and how the limit at negative infinity is related to the limit at the origin from the left.
There are three types of asymptotes:
-
Horizontal asymptotes
are lines
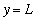 where
where
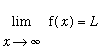 or
or
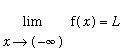 .
.
-
Oblique asymptotes
are lines
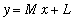 where
where
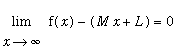 or
or
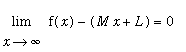 .
.
(Technically, a horizontal limit is an oblique asymptote with
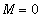 .)
.)
-
Vertical asymptotes
are lines
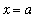 where
where
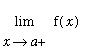 or
or
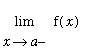 is infinite (either infinity or negative infinity).
is infinite (either infinity or negative infinity).
What's Next?
To practice the skills discussed in this lesson, work the online practice problems. Start the
online homework assignment only after you are confident with your skills with infinite limits. To conclude, complete the
textbook homework assignment.
The
Continuity lesson will apply almost all of the concepts introduced in the other lessons in
Unit 1. The ideas in this lesson are simple. The theoretical results that follow from the definition of continuity are critical for success in the later units in this course. The first theoretical application of continuity is the
Intermediate Value Theorem lesson.
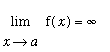 . That is, for values of
. That is, for values of
![]() near
near
![]() , all of the function values must be increasing without bound. For one-sided limits values of
, all of the function values must be increasing without bound. For one-sided limits values of
![]() are chosen from only one side of the the limit point. In many ways limits at infinity are the easiest to understand; that is where the discussion begins.
are chosen from only one side of the the limit point. In many ways limits at infinity are the easiest to understand; that is where the discussion begins.
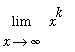 with
with
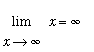 . Think about what this limit means: as the values of the independent varaiable increase without bound, the function values also increase without bound. Since the function is the identity function, its values are the same as the independent variable. With this result the Identity Law for limits (see the
. Think about what this limit means: as the values of the independent varaiable increase without bound, the function values also increase without bound. Since the function is the identity function, its values are the same as the independent variable. With this result the Identity Law for limits (see the
![limit(x^k,x = infinity) = PIECEWISE([infinity, `k > 0`],[1, `k = 0`],[0, `k < 0`])](images/LimitInfinite14.gif)
![[Maple Plot]](images/LimitInfinite15.gif)
![limit(x^k,x = -infinity) = PIECEWISE([infinity, `k = p/q > 0 with p even and q odd`],[-infinity, `k=p/q > 0 with p and q both odd`],[1, `k = 0`],[0, `k = p/q < 0 with q odd`],[`d.n.e.`, `k=p/q with q e...](images/LimitInfinite16.gif)
![[Maple Plot]](images/LimitInfinite18.gif)
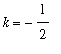 do not appear in the plot for
do not appear in the plot for
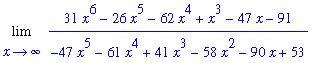
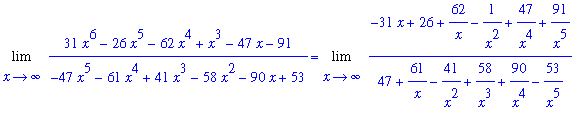
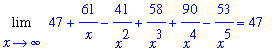
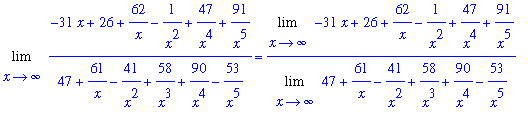
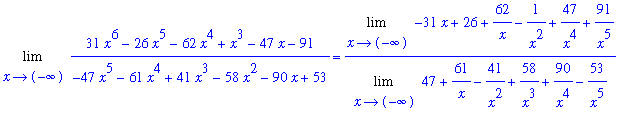
![[Maple Plot]](images/LimitInfinite32.gif)
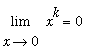 whenever
whenever
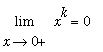 but the two-sided limit does not exist.) What happens to negative powers of x near the origin?
but the two-sided limit does not exist.) What happens to negative powers of x near the origin?
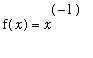 =
=
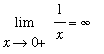
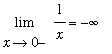
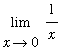 does not exist.
does not exist.
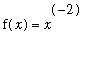 =
=
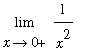 =
=
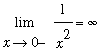 and so the corresponding two-sided limit does exist
and so the corresponding two-sided limit does exist
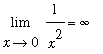 .
.
![limit(x^k,x = 0,right) = PIECEWISE([0, `k > 0`],[1, `k = 0`],[infinity, `k < 0`])](images/LimitInfinite61.gif)
![limit(x^k,x = 0,left) = PIECEWISE([0, `k = p/q > 0 with q odd`],[1, `k = 0`],[-infinity, `k = p/q < 0 with p and q both odd`],[infinity, `k = p/q < 0 with p even and q odd`],[`d.n.e.`, `k = p/q with q ...](images/LimitInfinite62.gif)
![[Maple Plot]](images/LimitInfinite63.gif)
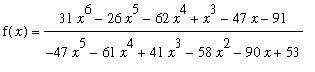
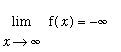 and
and
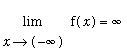 . These analytic results were supported by a plot of the function for -10 <
. These analytic results were supported by a plot of the function for -10 <
![[Maple Plot]](images/LimitInfinite78.gif)
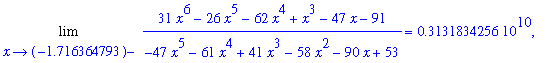
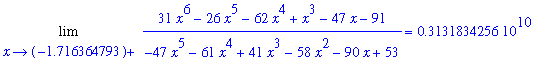
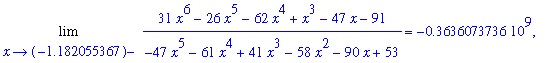
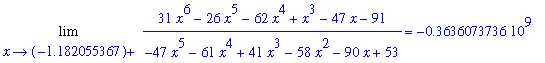
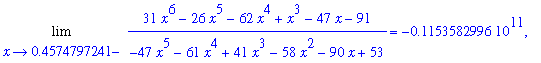
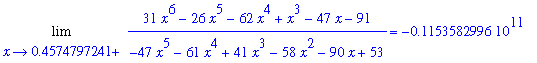
![[Maple Plot]](images/LimitInfinite86.gif)
![[Maple Plot]](images/LimitInfinite93.gif)
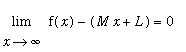 or
or
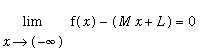 .
.
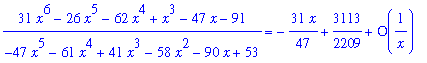
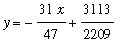 .
.
![[Maple Plot]](images/LimitInfinite106.gif)
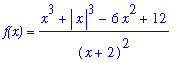
![[Maple Plot]](images/LimitInfinite110.gif)
![(x^3+abs(x)^3-6*x^2+12)/(x+2)^2 = PIECEWISE([2*(x^3-3*x^2+6)/(x+2)^2, 0 < x],[-6*(x^2-2)/(x+2)^2, x < 0])](images/LimitInfinite111.gif)
![[Maple Plot]](images/LimitInfinite115.gif)
![limit(x^k,x = infinity) = PIECEWISE([infinity, `k > 0`],[1, `k = 0`],[0, `k < 0`])](images/LimitInfinite116.gif)
![limit(x^k,x = -infinity) = PIECEWISE([infinity, `k = p/q > 0 with p even and q odd`],[-infinity, `k=p/q > 0 with p and q both odd`],[1, `k = 0`],[0, `k = p/q < 0 with q odd`],[`d.n.e.`, `k=p/q with q e...](images/LimitInfinite117.gif)
![limit(x^k,x = 0,right) = PIECEWISE([0, `k > 0`],[1, `k = 0`],[infinity, `k < 0`])](images/LimitInfinite118.gif)
![limit(x^k,x = 0,left) = PIECEWISE([0, `k = p/q > 0 with q odd`],[1, `k = 0`],[-infinity, `k = p/q < 0 with p and q both odd`],[infinity, `k = p/q < 0 with p even and q odd`],[`d.n.e.`, `k = p/q with q ...](images/LimitInfinite119.gif)
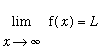 or
or
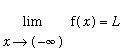 .
.
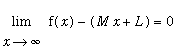 or
or
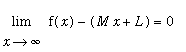 .
.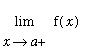 or
or
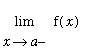 is infinite (either infinity or negative infinity).
is infinite (either infinity or negative infinity).