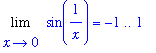LimitIntuitive.mws
Conceptual Understanding of the Limit
| > |
restart;
with( plots ):
|
Warning, the name changecoords has been redefined
Lesson Overview
The word "limit" is used in a variety of everyday circumstances. For example, all of us have heard a parent say "You are pushing the limit of my patience!". The intuitive mathematical definition is very similar. The basic idea is that the behavior of a function near a point can be very different from what happens directly at the point. In this lesson our objective is to begin to develop an intuitive mathematical definition about limits. We will first find limits from a graph then develop some basic techniques for the analytic evaluation of limits. These techniques will be combined to develop the concepts of one-sided limits and to support an initial look at two special trigonometric limits. The lesson concludes with a short reminder that graphs and tables of values can be misleading.
Definition (Intuitive Definition of Limits)
When we say that
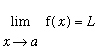 we mean that for all values of
we mean that for all values of
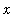 near (but different from)
near (but different from)
 , then the function values
, then the function values
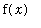 are all near
are all near
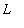 .
.
Outline
-
Graphical Evaluation of Limits
-
Basic Analytic Methods
-
Piecewise-Defined Functions and One-Sided Limits
-
Two Special Trigonometric Limits
-
Graphs and Tables can be Misleading
-
Limits for Oscillating Functions
Graphical Evaluation of Limits
The first step to understanding limits is to be able to identify limits from a graph of a function y = f(x). Once that is mastered it becomes necessary to determine limits from an algebraic description of the function. This is simplest when the function is defined at the limit point and there are no "problems" at the limit point.
You must be aware that this method is not foolproof. The most common "problems" that arise are division by zero and even roots of negative numbers.
This concept is illustrated in Example 1.
Example 1:
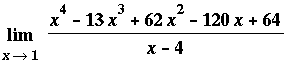
| > |
f1 := ( x^4 - 13*x^3 + 62*x^2 - 120*x + 64 ) / ( x - 4 ):
f(x) = f1;
|
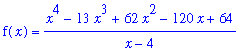
Prior to evaluating any limits, it is adviseable to plot the function. In this case, notice that the function is not defined for x=4.
| > |
p1 := display( [plot( f1, x=0..3.95 ),
plot( f1, x=4.05..6 ),
pointplot( [4,8], symbol=circle, symbolsize=18),
pointplot( [1,2], symbol=cross, symbolsize=18, color=blue)] ):
display( p1, title="Example 1: Plot of y=( x^4 - 13*x^3 + 62*x^2 - 120*x + 64 ) / ( x - 4 ) on [0,6]" );
|
![[Maple Plot]](images/LimitIntuitive8.gif)
The first attempt when evaluating a limit is to attempt to evaluate the function at the limit point. In this case, the function is defined at
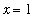 (see the blue cross in the above plot), and the value of the function at
(see the blue cross in the above plot), and the value of the function at
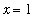 is
is
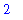
Based on this computation, and the graph, it appears as though
| > |
Limit( f1, x=1 ) = eval( f1, x=1 );
|
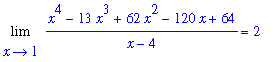
To confirm this result, note that Maple reports the value of this limit to be
| > |
Limit( f1, x=1 ) = limit( f1, x=1 );
|
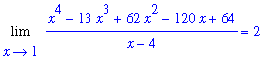
The same technique could be applied to all other limit points --- except
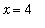 . At
. At
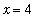 this function is not defined. From the graph it is clear that all function values close to
this function is not defined. From the graph it is clear that all function values close to
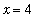 approach the same value, namely 5. An analytic derivation for this result will be developed next.
approach the same value, namely 5. An analytic derivation for this result will be developed next.
Basic Analytic Methods
The typical "problem" that prevents the direct evaluation of the function at the limit point is "division by zero".
If the function is a rational function and the numerator is also zero at the limit point, say
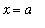 , then (
, then (
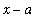 ) must be a common factor of both numerator and denominator. After cancellation of all common factors, direct evaluation can be retried.
) must be a common factor of both numerator and denominator. After cancellation of all common factors, direct evaluation can be retried.
This is illustrated in Example 2.
Example 2:
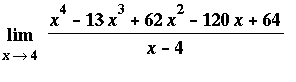
| > |
f1 := ( x^4 - 13*x^3 + 62*x^2 - 120*x + 64 ) / ( x - 4 ):
f(x) = f1;
p1 := display( [ plot( f1, x=0..3.95 ),
plot( f1, x=4.05..6 ),
pointplot( [4,8], symbol=circle, symbolsize=18) ] ):
|
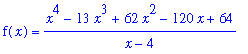
The first attempt when evaluating a limit is to evaluate the function at the limit point. In this case, the function is not defined at
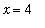 :
:
Error, numeric exception: division by zero
Upon closer inspection it is seen that both numerator and denominator are zero when
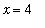 :
:
| > |
eval( numer(f1), x=4 );
eval( denom(f1), x=4 );
|
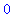
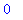
This means that we can factor (
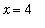 ) from both numerator and denominator. The resulting function is
) from both numerator and denominator. The resulting function is
| > |
n1 := factor( numer(f1) );
d1 := factor( denom(f1) );
f2 := n1/d1;
|
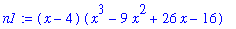
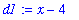
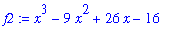
The new function,
f2
, is identical to
f1
except that it is defined at
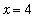 . This can be illustrated in a plot.
. This can be illustrated in a plot.
| > |
p2 := plot( f2, x=0..6, color=green, thickness=3 ):
display( [p1,p2], title="Example 2: Plot of\ny=(x^4-13*x^3+62*x^2-120*x+64)/(x-4) and y=x^3-9*x^2+26*x-16\non [0,6]" );
|
![[Maple Plot]](images/LimitIntuitive30.gif)
The goal of this example is to illustrate that changing the definition of the function at one point does not change the value of the limit:
| > |
Limit( f1, x=4 ) = Limit( f2, x=4 );
|
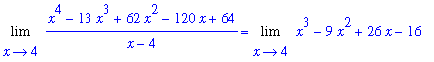
The limit can be evaluated as in the previous example:
| > |
Limit( f2, x=4 ) = eval( f2, x=4 );
|
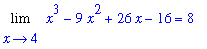
This result appears to be consistent with the graphical information. Moreover, Maple reports the value of the original limit to be
| > |
Limit( f1, x=4 ) = limit( f1, x=4 );
|
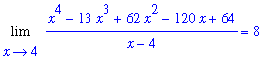
Note that if the numerator is not zero at the limit point then no cancellation is possible. This situation will be dealt with in detail in the
Infinite Limits lesson.
Piecewise-Defined Functions and One-Sided Limits
Piecewise-defined functions present a new wrinkle beyond that encountered with rational functions. The difficulty with a piecewise-defined function arises when the limit point is also a transition point between two parts of the definition of the function.
In these situations it is not generally possible to algebraically simplify the problem so that it can be evaluated by direct substitution. Instead, the two different directions in which the limit point can be approached lead to the two one-sided limits.
Each of these limits is usually fairly simple to evaluate as they involve only one part of the definition of the piecewise-defined function. If these two limits exist AND have the same value, then the two-sided limit exists and has the same value as the two one-sided limits.
Examples 3 and 4 illustrate these ideas.
Example 3:
![Limit(PIECEWISE([-x^2+2, x < 1],[sqrt(x-1)-2*x/3+2, 1 <= x]),x = 1)](images/LimitIntuitive34.gif)
| > |
f3 := piecewise( x<1, -x^2+2, x>=1, sqrt(x-1)-2*x/3+2 ):
f(x) = f3;
|
![f(x) = PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x])](images/LimitIntuitive35.gif)
As before, we begin with a plot
| > |
p3 := plot( f3, x=0..6, discont=true ):
display( p3, view=[0..6,0..3], title="Example 3: Plot of a piecewise-defined function with a jump at x=1" );
|
![[Maple Plot]](images/LimitIntuitive36.gif)
This picture convincingly shows that the (two-sided) limit of this function does not exist at
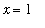 . This is true even though there is no problem directly evaluating the function at the limit point:
. This is true even though there is no problem directly evaluating the function at the limit point:
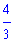
but Maple reports that the limit does not exist
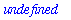
To understand why this limit does not exist, consider the two one-sided limits:
| > |
q1 := Limit( f3, x=1, left ) = Limit( -x^2+2, x=1 ):
q1,`` = eval( -x^2+2, x=1 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1,left) = Limit(-x^2+2,x = 1), `` = 1](images/LimitIntuitive40.gif)
| > |
q2 := Limit( f3, x=1, right ) = Limit( sqrt(x-1)-2*x/3+2, x=1 ):
q2;
`` = eval( sqrt(x-1)-2*x/3+2, x=1 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1,right) = Limit((x-1)^(1/2)-2/3*x+2,x = 1)](images/LimitIntuitive41.gif)
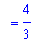
The fact that the one-sided limits have different values explains why the two-sided limit does not exist. This result is confirmed by Maple:
| > |
q3 := Limit( f3, x=1 ):
q3 = value( q3 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1) = undefined](images/LimitIntuitive43.gif)
Example 4:
![Limit(PIECEWISE([-x^2+2, x < 1],[sqrt(x-1)-x+2, 1 <= x]),x = 1)](images/LimitIntuitive44.gif)
| > |
f4 := piecewise( x<1, -x^2+2, x>=1, sqrt(x-1)-x+2 ):
f(x) = f4;
|
![f(x) = PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x])](images/LimitIntuitive45.gif)
This function looks very similar to the function in Example 3. A plot shows that there is, however, a fundamental difference:
| > |
p4 := plot( f4, x=0..6, discont=true ):
display( p4, view=[0..6,0..3], title="Example 4: Plot of piecewise-defined function without a jump" );
|
![[Maple Plot]](images/LimitIntuitive46.gif)
This picture suggests that the values of this function on either side of
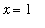 approach the same value -- namely, 1. To confirm this, look at the two one-sided limits:
approach the same value -- namely, 1. To confirm this, look at the two one-sided limits:
| > |
q1 := Limit( f4, x=1, left ) = Limit( -x^2+2, x=1 ):
q1;
`` = eval( -x^2+2, x=1 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1,left) = Limit(-x^2+2,x = 1)](images/LimitIntuitive48.gif)
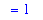
| > |
q2 := Limit( f4, x=1, right ) = Limit( sqrt(x-1)-x+2, x=1 ):
q2;
`` = eval( sqrt(x-1)-x+2, x=1 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1,right) = Limit((x-1)^(1/2)-x+2,x = 1)](images/LimitIntuitive50.gif)
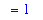
The fact that the one-sided limits exist and have the same value permits us to conclude the two-sided limit does exist and has value 1. Maple confirms this conclusion:
| > |
q3 := Limit( f4, x=1 ):
q3 = value( q3 );
|
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1) = 1](images/LimitIntuitive52.gif)
Two Special Trigonometric Limits
The limits
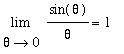 and
and
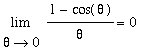
will arise repeatedly throughout this course. These limits will be discussed from graphically in this lesson and rigorously derived with the assistance of some geometry in the
Limits of Trigonometric Functions lesson. Graphical justification for these limits is obtained from the following plots.
| > |
p1 := plot( sin(theta)/theta, theta=-4*Pi..4*Pi,
title="Plot of y=sin(theta)/theta on [-4*Pi,4*Pi]" ):
p1;
|
![[Maple Plot]](images/LimitIntuitive55.gif)
| > |
p2 := plot( (1-cos(theta))/theta, theta=-4*Pi..4*Pi,
title="Plot of y=(1-cos(theta))/theta on [-4*Pi,4*Pi]" ):
p2;
|
![[Maple Plot]](images/LimitIntuitive56.gif)
These limits are very special. Any deviation from these forms must be dealt with carefully. If a limit does not exactly fit one of these forms, algebraic substitutions and simplifications can be used in the attempt to transform the limit into one of these special limits. Example 5 illustrates how a problem can be broken down into one of these special limits.
Example 5:
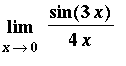
| > |
f5 := sin(3*x)/(4*x):
f(x) = f5;
|
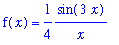
Observe that this function is not defined for
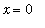 and no amount of factoring or other manipulation can eliminate the "division by zero" problem at
and no amount of factoring or other manipulation can eliminate the "division by zero" problem at
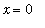 . In situations like this the graph is even more important.
. In situations like this the graph is even more important.
| > |
p5 := display( [ plot( f5, x=-Pi..-0.05 ),
plot( f5, x=0.05..Pi ),
pointplot( [0,0.75], symbol=circle, symbolsize=18) ] ):
display( p5, view=[-Pi..Pi,-0.25..1], title="Plot of y=sin(3*x)/(4*x) on [-Pi,Pi]" );
|
![[Maple Plot]](images/LimitIntuitive61.gif)
This plot suggests that the limit should exist and its value should be around 0.75. To gather further evidence in support of this observation, create a table of values for the function evaluated close to zero.
| > |
a := 0:
H := [ 1.0, 0.5, 0.1, 0.01, 0.001, 0.0001, 0.00001 ]:
|
For values converging to
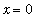 from the left of the limit point:
from the left of the limit point:
| > |
xL := [seq( a-h, h=H )]:
bodyL := seq( < X | eval(f5,x=X) >, X=xL ):
header := < theta | f(theta) >, <`_______` | `____________` >:
< header, bodyL >;
|

This suggests that the one-sided limit from the left exists and has value
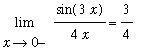 .
.
Similarly, for values converging to
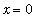 from the right of the limit point:
from the right of the limit point:
| > |
xR := [seq( a+h, h=H )]:
bodyR := seq( < X | eval(f5,x=X) >, X=xR ):
< header, bodyR >;
|

supports the claim that the one-sided limit from the right exists and has value
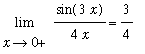 .
.
The existence and agreement of both one-sided limits is additional support for the claim that the value of the (two-sided) limit is 3/4.
Note:
This argument is
not
a complete justification of the evaluation of this limit. The problem is that a table of function values is never sufficient to justify the evaluation of a limit. The complete evaluation of this limit will be discussed in the
Limits of Trigonometric Functions lesson. Some of the problems that can arise from the use of a table or graph to evaluate a limit are discussed next in this lesson.
Graphs and Tables can be Misleading
A graph is not always sufficient to determine a limit. Almost all computer-generated graphs are really just plots of a collection of points connected to form the curve. If the collection of points is not done wisely, some important information about the function will be missing from the plot. By the same reasoning a table of values can be misleading.
These obstacles can oftentimes be overcome by the selection of an appropriate viewing window for the function or the selection of an appropriate set of points to use to create the table.
This is illustrated in Example 6.
Example 6:
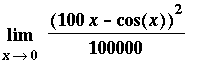
| > |
f6 := (100*x - cos(x))^2/100000:
f(x) = f6;
|
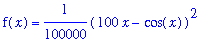
As usual, begin with a plot of the function. The graph of
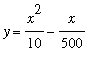 is included for comparison purposes.
is included for comparison purposes.
| > |
p6 := plot( [f6,x^2/10-x/500], x=-1..1, thickness=[1,3] ):
display( p6, title="Plot of y=(100*x-cos(x))^2/100000 and y=x^2/10-x/500 on [-1..1]" );
|
![[Maple Plot]](images/LimitIntuitive71.gif)
The graph of this function is indistinguishable from the graph of
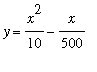 on this interval.
on this interval.
If we create tables of function values for this function to the left and right of
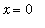 , we might obtain
, we might obtain
| > |
a := 0:
H := [ 1.0, 0.5, 0.1, 0.01 ]:
xL := [seq( a-h, h=H )]:
xR := [seq( a+h, h=H )]:
|
For values converging to
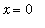 from the left of the limit point:
from the left of the limit point:
| > |
header := < `x` | `f(x)` >, < `_____` | `_______________` >:
bodyL := seq( < X | eval( f6, x=X ) >, X= a-H ):
tableL := < header, bodyL >:
|
and from the right of the limit point:
| > |
bodyR := seq( < X | eval( f6, x=X ) >, X= a+H ):
tableR := < header, bodyR >:
tableL, tableR;
|

The most likely conjecture about this limit based on these (short) lists of function values is that
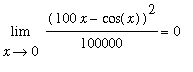 . However, this is incorrect.
. However, this is incorrect.
This limit can be evaluated by direct evaluation of this function at
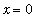 . This operation yields
. This operation yields
| > |
q1 := Limit( f6, x=0 ) = eval( f6, x=0 ):
q1;
`` = evalf( eval(f6,x=0) );
|
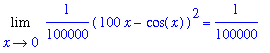
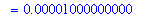
which is in agreement with Maple
| > |
q2 := Limit( f6, x=0 ):
q2 = value( q2 );
|
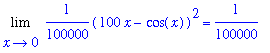
Thus, the initial picture and subsequent tables were all misleading. In this case if we zoom in on the graph to the interval [-0.01, 0.01 ], the functions are seen to be quite different.
| > |
p6z := plot( [f6,x^2/10-x/500], x=-0.01..+0.03, thickness=[1,3] ):
display( p6z, title="Plot of y=(100*x-cos(x))^2/100000 and y=x^2/10-x/500 on [-0.01..0.03]" );
|
![[Maple Plot]](images/LimitIntuitive81.gif)
The point of this example is to illustrate that neither a graph nor a table of function values can completely justify the evaluation of a limit. Graphs of the function and corresponding tables of values can be useful but are only the first step. Hopefully, the information gathered from the table of function values suggests other methods and techniques for justifying the evaluation of a limit. The rigorous evaluation of limits is discussed in the Precise Definition of the Limit lesson.
Limits for Oscillating Functions
The fundamental trigonometric functions are the sine and cosine functions. These functions are periodic (with period
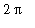 ). This means the function values repeat every
). This means the function values repeat every
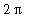 units, as shown in the following plot.
units, as shown in the following plot.
| > |
plot( [sin(theta), cos(theta)], theta=-3*Pi..3*Pi,
color=[red,blue], scaling=constrained,
title="Three periods of the sine and cosine functions",
legend=["y=sin(theta)","y=cos(theta)"] );
|
![[Maple Plot]](images/LimitIntuitive84.gif)
All periodic functions oscillate. When composed with other functions, these oscillations can be problematic in limit problems. If a function oscillates with a fixed amplitude, this function will not converge as the variable increases (or decreases) without bound. If, however, the amplitude decreases then there is a chance the limit does exist. (This type of limit will be discussed in detail in the Limits at Infinity leson.)
Example 7 contains an example with oscillations near a finite limit point.
Example 7:
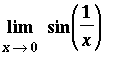
| > |
f7 := sin(1/x):
f(x) = f7;
|
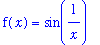
This function is not defined at
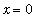 . A graph of the function that avoids the problems at the origin shows that this function oscillates between -1 and 1.
. A graph of the function that avoids the problems at the origin shows that this function oscillates between -1 and 1.
| > |
p7 := display( [ plot( f7, x=-2/Pi..-0.01 ),
plot( f7, x= 0.01.. 2/Pi ) ] ):
display( p7, title="Plot of y=sin(1/x) on [-2/Pi,2/Pi]" );
|
![[Maple Plot]](images/LimitIntuitive88.gif)
Observe that the period of the oscillations increases as the points move closer to the origin -- from both the left and the right. This suggests that the function will take on all values between -1 and 1 infinitely often for points close to
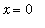 . In particular, the value of the function does not approach a single point and the limit (two-sided or one-sided) does not exist.
. In particular, the value of the function does not approach a single point and the limit (two-sided or one-sided) does not exist.
Observe that Maple's evaluation of this limit informs us that the limit does not exist and the reason for this is that the values oscillates between -1 and 1.
| > |
q1 := Limit( f7, x=0 ):
q1 = value( q1 );
|
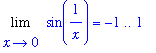
Lesson Summary
In this lesson we have developed the following general procedure for evaluating limits:
A Concept-Based Approach to Evaluating
-
The first step in most limit problems should be to graph or otherwise visualize the function on an appropriate interval.
-
The easiest limits to compute are the ones where it is possible to simply evaluate the function at the limit point. The graph can
suggest
if this is permissible for a problem.
-
Division by zero is one problem that can prevent the direct evaluation of a limit.
-
Factorization and cancellation of powers of (
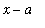 ) can lead to an equivalent limit that can be computed by direct evaluation. (This method works because it changes the value of the function only at
) can lead to an equivalent limit that can be computed by direct evaluation. (This method works because it changes the value of the function only at
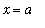 and the value of the function at this point does not influence the existence of the limit or its value.)
and the value of the function at this point does not influence the existence of the limit or its value.)
-
A two-sided limit exists only when both one-sided limits exist and have the same value. If both one-sided limits exist but have different values, the function experiences a jump at this point and the (two-sided) limit does not exist.
-
There are two special limits involving trigonometric functions. These special limits can be used to evaluate other trigonometric limits, including some that will appear in the discussion of derivatives in
Unit 2.
-
Do not become complacent when using a graph or table of function values to evaluate a limit. If not chosen wisely, they can be misleading!
What's Next?
Now that you have completed this lesson, you should practice your limit evaluation skills with the
online homework assignment. Note there are practice sessions for specific topics, a general practice session for problems related to this lesson, and a graded homework assignment. Work enough practice problems to master these concepts, then complete the online homework assignment and the
assigned problems from the text. Independent practice sessions for a specific topic are also provided.
The next lesson uses the ideas presented in this lesson to develop a
Precise Definition of the Limit.
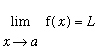 we mean that for all values of
we mean that for all values of
![]() near (but different from)
near (but different from)
![]() , then the function values
, then the function values
![]() are all near
are all near
![]() .
.
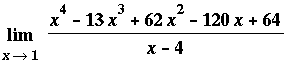
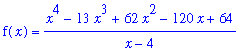
![[Maple Plot]](images/LimitIntuitive8.gif)
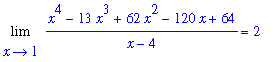
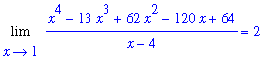
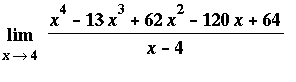
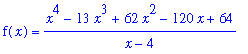
![[Maple Plot]](images/LimitIntuitive30.gif)
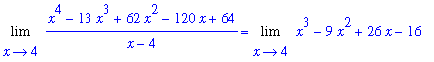
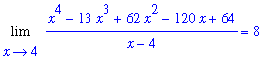
![Limit(PIECEWISE([-x^2+2, x < 1],[sqrt(x-1)-2*x/3+2, 1 <= x]),x = 1)](images/LimitIntuitive34.gif)
![f(x) = PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x])](images/LimitIntuitive35.gif)
![[Maple Plot]](images/LimitIntuitive36.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1,left) = Limit(-x^2+2,x = 1), `` = 1](images/LimitIntuitive40.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1,right) = Limit((x-1)^(1/2)-2/3*x+2,x = 1)](images/LimitIntuitive41.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-2/3*x+2, 1 <= x]),x = 1) = undefined](images/LimitIntuitive43.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[sqrt(x-1)-x+2, 1 <= x]),x = 1)](images/LimitIntuitive44.gif)
![f(x) = PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x])](images/LimitIntuitive45.gif)
![[Maple Plot]](images/LimitIntuitive46.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1,left) = Limit(-x^2+2,x = 1)](images/LimitIntuitive48.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1,right) = Limit((x-1)^(1/2)-x+2,x = 1)](images/LimitIntuitive50.gif)
![Limit(PIECEWISE([-x^2+2, x < 1],[(x-1)^(1/2)-x+2, 1 <= x]),x = 1) = 1](images/LimitIntuitive52.gif)
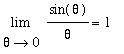 and
and
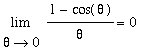
![[Maple Plot]](images/LimitIntuitive55.gif)
![[Maple Plot]](images/LimitIntuitive56.gif)
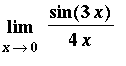
![[Maple Plot]](images/LimitIntuitive61.gif)

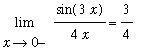 .
.

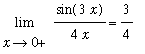 .
.
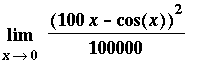
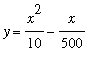 is included for comparison purposes.
is included for comparison purposes.
![[Maple Plot]](images/LimitIntuitive71.gif)
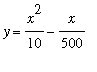 on this interval.
on this interval.

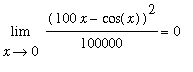 . However, this is incorrect.
. However, this is incorrect.
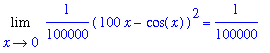
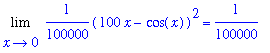
![[Maple Plot]](images/LimitIntuitive81.gif)
![[Maple Plot]](images/LimitIntuitive84.gif)
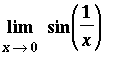
![[Maple Plot]](images/LimitIntuitive88.gif)