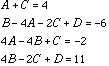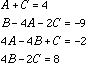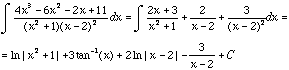Math 142
Partial Fractions Examples
- Integrate using partial fractions
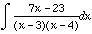
We have, 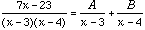 for some A and B.
for some A and B.
So, 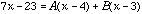
Now letting x=3, we get A=2; and letting x=4, we get B=5.
So, 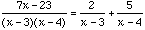 .
.
Hence, 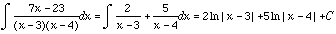
Note that we can simpliy this last expression to 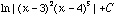 .
.
Two hydrogen atoms were walking along the street one day, and suddenly the one
of the right says: Ohmigosh! I lost an electron!
The one on the left says.. "Are you sure??"
The one on the right replies: "Yes, yes! I'm positive!"
Suppose we want to express 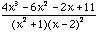 as a sum of partial fractions.
as a sum of partial fractions.
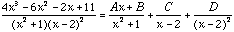
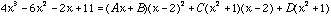
Now letting x=2 on both sides, we see that 15 = 5D, and so D = 3.
Now expanding the Right-Hand-Side we get
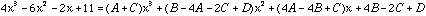
So, 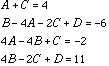
Substituting D=3 into these gives,
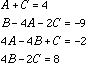
Solving these three equations simultaneously gives A=2, B=3, C=2 (and previously D=3)
So, 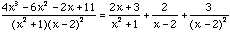 , and we have
, and we have
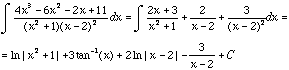
Express 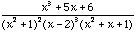 a sum of partial fractions - but do not solve for the constants.
a sum of partial fractions - but do not solve for the constants.
Answer: 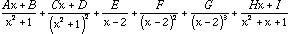
Practice does not make perfect;
perfect practice makes perfect.
VINCE LOMBARDI
If the only tool you have is a hammer,
you tend to see every problem as a nail.
ABRAHAM MASLOW
Express as a sum of partial fractions (you must solve for the constants). 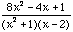
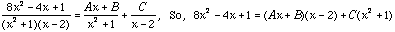
Let x=2 on both sides and we get, 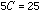 , so
, so 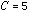 .
.
Also, expanding the product on the right, 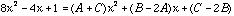
Now compare the coefficients on both sides of this identity.
So, 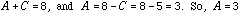
And, 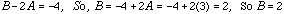
So, 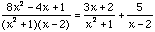
It's like deja-vu, all over again.
YOGI BERRA
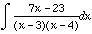
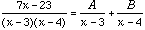 for some A and B.
for some A and B.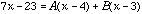
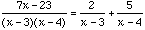 .
.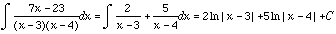
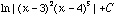 .
.