Elementary Differential Equations
Fall 2002
Professor
Robert Sharpley
Meets: MWF 9:05 - 9:55 in LeConte College 405
Instructor Information
Office: LeConte 313 D
Office Hours: MWF 10-11, or
by appointment.
| MATH 242 Section 1
Elementary Differential Equations Fall 2002 Professor
Robert Sharpley
Instructor Information
|  |
|
|
|
||
|
Loaded at 9:45 am on Friday - Dec. 13 Have a good Holidays! |
Course Information
Catalogue Description: Ordinary differential equations of first order, higher order linear equations, Laplace transform methods, series methods; numerical solution of differential equations. Applications to physical sciences and engineering. Introduction to programming desirable.
Course Topics: The course will cover the general topics contained in chapters 1-5, 7, and 9 of the text. These topics include
Grading scheme:
Homework will be assigned on a regular basis but will not be collected.
There will, however, be daily/weekly quizzes over the assigned
homework and the lectures which will be collected and graded. This
will make up 15% of the final grade.
There will be 3 scheduled tests during the semester. No makeup tests will
be given, but the lowest grade of the three test grades will be
dropped and each of the two remaining tests will account for 25% of
the course grade.
The Final Exam will count 35%.
Attendance: Classroom attendance is required according to official university policy.
Important Course Dates:
|
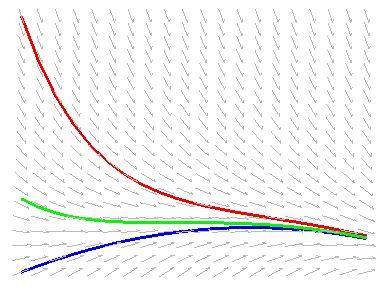
![]() Computational Work Sheets and Course Supplements
Computational Work Sheets and Course Supplements
|
|
||
![[USC logo]](usclogo.gif) |
 |
|
| This page maintained by Robert Sharpley
(sharpley@math.sc.edu)
and last updated August 16, 2002.
This page ©2002-2003, The Board of Trustees of the University of South Carolina. URL: http://www.math.sc.edu/~sharpley/math242 |
||