Math 241.01 - Vector Calculus
Final Exam - April 30, 1997
Name:
Directions: Clearly mark your answer and show your
work for full credit.
- If u = < 1,2,-1
> and v = < 0,3,1
> , then determine
- a.)
- u ·v
- b.)
- u ×v
- c.)
- projection of u onto the direction of v
- d.)
- 2u -3v
- Compute the equation of the plane that passes through the points (1,0,-1),
(2,3,1), and (3,2,0).
- Consider the function f(x,y) = xy2-6x2-3y2
- a.)
- Determine all critical points for f.
- b.)
- Apply the second derivative test to classify all critical points as
local maxima, minima, or saddle points.
- Let f(x,y) = [(2x-3y)/(x+1)].
- a.)
- Plot the level curve of f for c = 1.
- b.)
- Compute the gradient of f at the point (4,1) and sketch it on the graph
in part (a).
- Show that the sphere x2+y2+z2-4y-2z+2
= 0 is perpendicular to the paraboloid 3x2+2y2-2z
= 1 at the point (1,1,2). (i.e. their tangent planes are perpendicular.)
- Let S be the tetrahedron determined by the coordinate planes and the
plane x+y+2z = 4.
- a.)
- Sketch and parameterize the region S.
- b.)
- Compute the integral
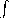
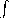
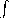 S
(y-x) dx dy dz
S
(y-x) dx dy dz
- Use cylindrical coordinates to compute the volume of the solid above
the xy-plane, below the surface z = xy and within the cylinder x2+y2
= 2x.
- Use the chain rule to compute [du/dt] where u = 2x2-xy+y3,
x = sin(t), and y = cos(t). (Do not simplify.)
- Show that curl (
 f)
º 0.
f)
º 0.
- Compute the line integral of f(x,y,z) = 2x+9z along the curve C given
by x = t, y = t2, and z = t3, 0 £
t £ 1.
- Let C be the semi-circle formed by the upper half of a circle of radius
2 and center the origin and diameter along the x-axis.
- a.)
- Compute
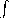 C
(y+1) dx+2x dy directly, using the definition of
the line integral, where C is oriented in the counter-clockwise direction.
C
(y+1) dx+2x dy directly, using the definition of
the line integral, where C is oriented in the counter-clockwise direction.
- b.)
- Use Green's theorem to evaluate the integral in part (a).
File translated from TEX by TTH,
version 1.2.
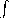
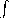
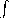 S
(y-x) dx dy dz
S
(y-x) dx dy dz 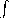 C
(y+1) dx+2x dy directly, using the definition of
the line integral, where C is oriented in the counter-clockwise direction.
C
(y+1) dx+2x dy directly, using the definition of
the line integral, where C is oriented in the counter-clockwise direction.