Introduction
This page is meant to be an introduction to neural networks. In no way will this be exhaustive, nor is this in any way standard, yet I will attempt to give proper motivation and plenty of pedagogical examples. I will also try my best to point out mathematical connections for the fields of Linear Algebra, Probability Theory, and Geometry. As well I will try to provide as many pictures as possible.
In many expositions for neural networks the authors give a historical point of view, mentinoing early failures. I will not being taking this perspective, instead I will be telling the story of how it appears now and attempt to frame this tale as:
"This is how it should naturally be..."
With that rant out of the way, just to avoid angry emails from machine learning super fans, I will note that neural networks would not even be a field of study without the semial work of Geoffrey Hinton, David Rumelhart, and Ronald Williams from Cognitive Modeling (1988): “Learning representations by back-propagating errors”
Before I begin I would feel remiss if I did not forewarn any potential reader.
WARNING:
This is written by an (Algebraic) Geometer, and as such it will be skewed to a geometric (or algebraic) point of view in most cases!
Neurological Motivation
The Brain is a miraculous innovation of nature made up of a 100 billion different extraordinary cells, known as neurons. When these neurons are introduced to outside stimuli they produce electrical and chemical signals which they pass to other neurons.
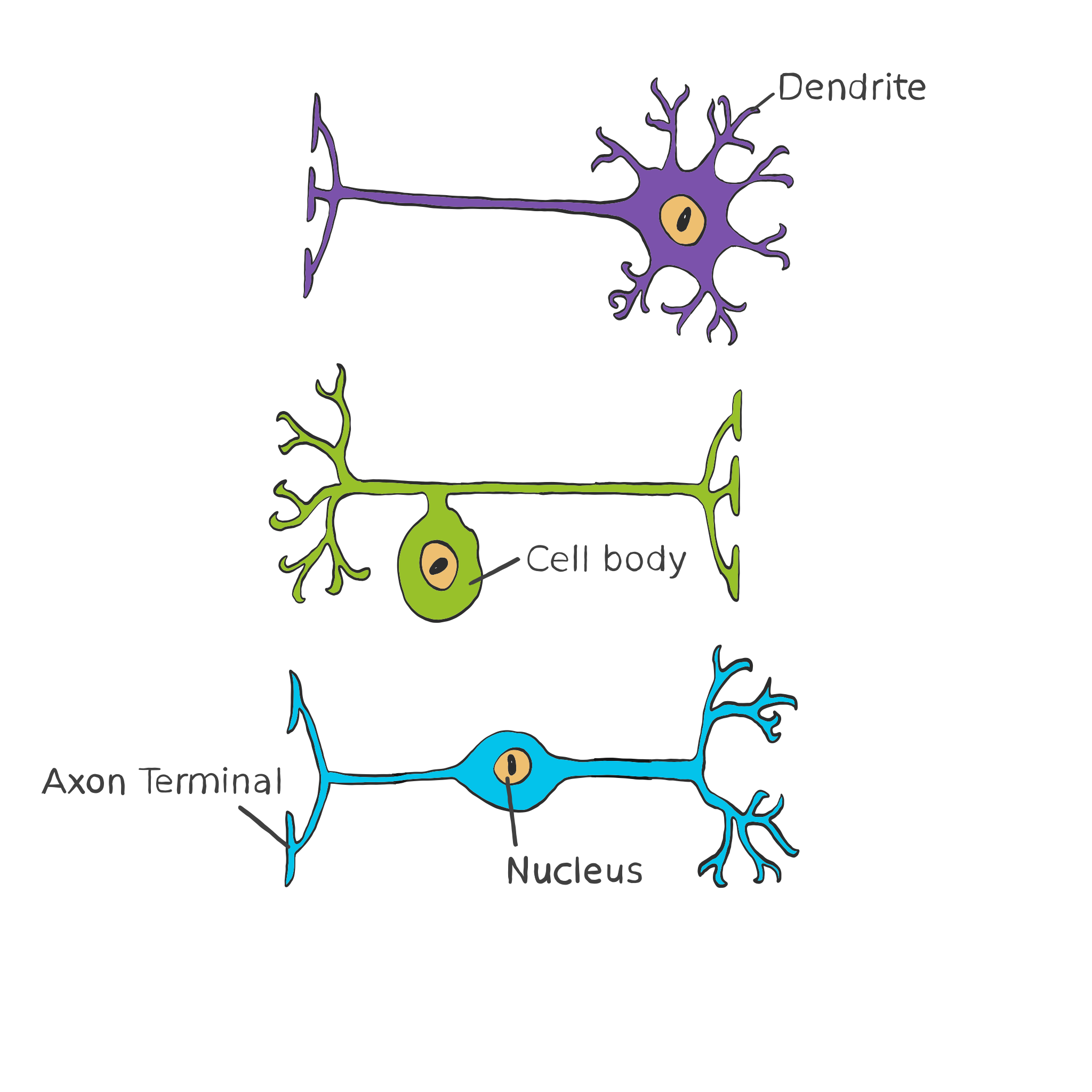
The neuron release chemicals from the Dendrite and recieve the chemical signals from other neurons with the Axon Terminal. For example when a mouse sees some cheese neurons in the brain 'communicate' with each other.

Take-Aways:
There are two ideas to take away from the process of neurons.
1. Many Neurons
The input (known as reception fields) from the eye isn't just sent to one neuron to make a decision it is sent to many neurons which in turn send it to many more neurons before the brain makes a decision on what it is seeing.
2. Probalistic
When one neuron sends a signal to another neuron the recieving neuron must decide if (and how much) to relay the message...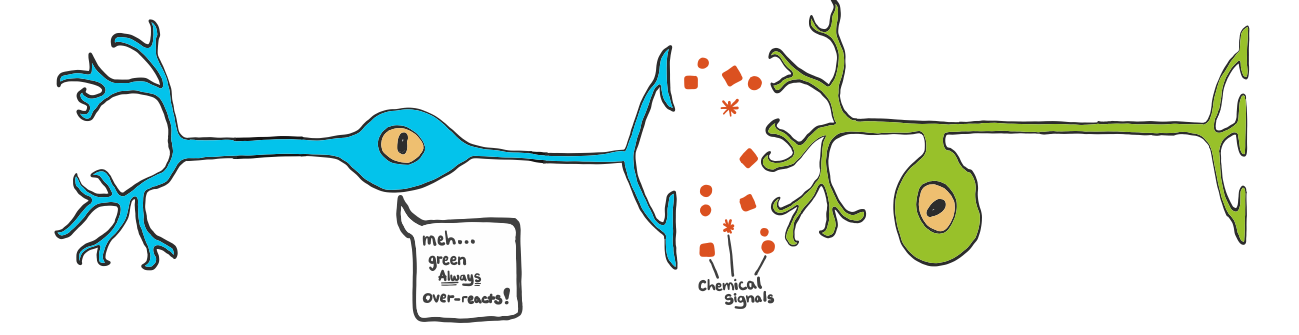
The choice of the blue neuron (pictured above) of what intensity to relay green's signal is probalistic in nature. Like blue could be thinking that green is only right 50% of the time.
It is this communication between neurons that creates ALL the power of the brain, from breathing, to deciding if you want to eat Froot Loops® or Cheerios® in the morning.
Pros and Cons of Neural Networks
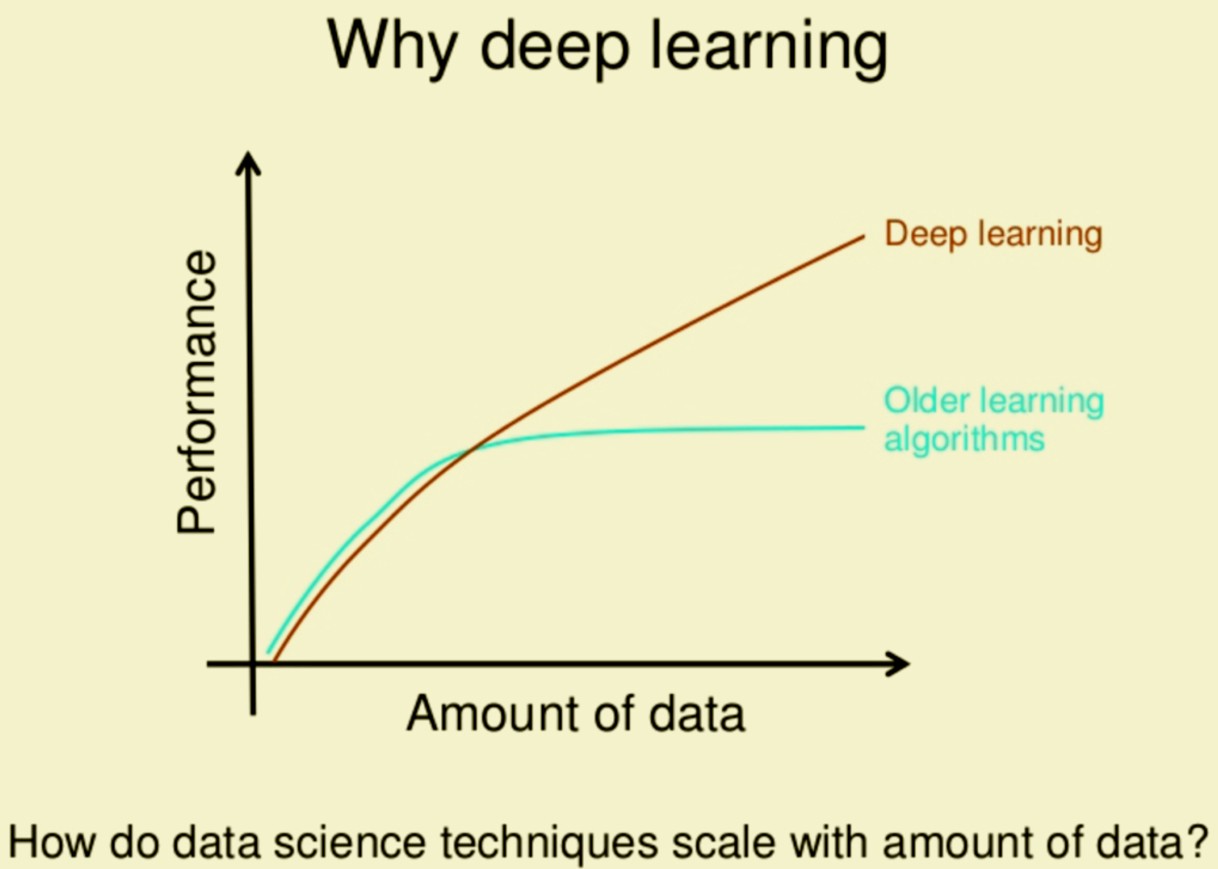
"The language and logic used by the brain must be essentially different than any known to humans"
I see this as if we as humans were to create something which works like a brain then we as humans perhaps would not be able to understand
To be Continued...
