Assignment #2: Norms and the SVD
Due: Friday, 9 February 1996
:

-
Graph the sets
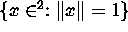 for the 1-, 2-, 4-, and
for the 1-, 2-, 4-, and
 -norms. (These are the unit balls for the different norms.)
-norms. (These are the unit balls for the different norms.)
-
Graph the set
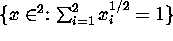 . Why is there no
. Why is there no
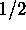 -norm? (Which of the defining properties of a norm is/are not satisfied?)
-norm? (Which of the defining properties of a norm is/are not satisfied?)
-
The version of showsvd that I wrote adds a rank-one update to the
image (matrix) at each step. Generalize the showsvd function so that
at each step the image is updated by a matrix with rank specified by the
user. Also, modify the titles to indicate relative error (in the 2-norm)
between the approximate and original images.
-
Use your new version of showsvd to determine the lowest rank
approximation which reproduces the original image with a 10%, 1%,
and 0.1% relative error (in the 2-norm). How much information is
needed to produce each of these approximations?
-
Try to be as efficient as possible in your implementation of showsvd.
In particular, use block matrix operations whenever possible. Matlab commands
for counting, and timing, operations include flops and cputime.
-
If you have any questions, please ask in class, in office hours, by e-mail,
 .
.
Douglas B. Meade
Last revision: Sat Jan 27 18:54:37 EST 1996


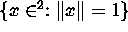 for the 1-, 2-, 4-, and
for the 1-, 2-, 4-, and
 -norms. (These are the unit balls for the different norms.)
-norms. (These are the unit balls for the different norms.)
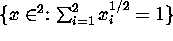 . Why is there no
. Why is there no
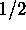 -norm? (Which of the defining properties of a norm is/are not satisfied?)
-norm? (Which of the defining properties of a norm is/are not satisfied?)
 .
.