Course Project
General Instructions
-
This project comes in three separate, but related, parts. The first part
of the project is to be a solo effort. The second and third components
will be group efforts.
-
Here's the basic idea. First, you will find an engineering or scientific
application of differential equations. The second component calls for
the group investigation of a specific application of ODEs in chemical
engineering. Each group will then choose one of their individual projects
for analysis; this is the third and final part of the project.
-
The report for each part of the project is worth 30 points. The distribution
of these points will be

The remaining points are based on the prompt selection of group members
(5 points) and a brief summary of the group experience (5 points).
Part I -- Design Your Own Project
-
The first part of the project is for you to identify an application of
differential equations in a discipline other than mathematics. Possible
sources for ideas for applications include your academic advisor and a
professor in an engineering or science course. Even if you have an idea
what you want to do, you must discuss your idea with a faculty member
(in addition to me).
-
The application must involve either i) a second-order initial value problem,
ii) a second-order boundary value problem, or iii) a system of initial value
problems.
-
I expect some of you will have similar projects. In fact, these common
interests will be beneficial when forming the groups for the other two
parts of the project.
-
Each student will prepare their own one-page project report for this
part of the project.
-
Each project report must contain all of the following: title, faculty
contact, non-mathematical project description (including specific questions
that need to be answered), the mathematical formulation of the problem,
(realistic) numerical values for any parameters and appropriate references
(at least one). A sample description is attached to this assignment.
-
I suggest at least two short meetings with your contact person. Decide on
a project in the first meeting. Then, after writing an initial draft of
the project, return for a second meeting to check that you have accurately
and completely described the project. (You may wish to make a copy of this
assignment to give to your contact person.)
-
Do not wait until the last week to begin working on this part of the
project. Remember that you will have to work around the schedule of
another faculty member.
-
The final report should be signed by your contact. (This is be worth 5 points
towards the technical correctness.)
-
Individual project descriptions are due no later than 5:00P.M.,
Friday, February 24, 1995.
Part 2 -- Consecutive Reactions in a Batch Reactor
-
This part of the project is to be worked on in groups of three or four
students. You may select your own partners. When selecting group members,
remember that you will have to have common times when you can meet.
-
Group selection must be completed by Friday, March 3, 1995. Anyone not
notifying me of their group selection by the deadline will be placed in
a group at random and will not receive their five (5) points for this
part of the assignment.
-
The objective of this component of the project is to investigate the
sample application included with this project assignment. Please consult
that description for the specific points to be considered.
-
One of your first steps should be the identification of all questions
that need to be answered. Next, determine what information will be needed
to answer these questions. Finally, use your knowledge of differential
equations to answer all relevant questions.
-
The bulk of the analysis should be performed with as much generality as
possible. In particular, do not assume particular values for the parameters
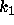 and
and 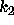 until you need to produce a plot. (If you analysis does
not apply for certain combinations of the parameters, be sure to mention
this.)
until you need to produce a plot. (If you analysis does
not apply for certain combinations of the parameters, be sure to mention
this.)
-
The parameter values I have selected are not realistic. They have been
selected to illustrate the different types of behaviors that can occur.
You should spend some time in the library researching this problem. In
particular, look for specific examples to which the model can be applied.
-
Keep good notes of your work. Remember the mistakes that you make, and
try to learn from them.
-
Be sure that each team member knows their responsibilities to the overall
team effort. All members of the team are expected to contribute to all parts
of the project. I will be looking for evidence of collaboration between
team members.
-
Typed reports are preferred. (I suggest using a word processor.) There
is no page requirement for the full report, just that you efficiently
report all your findings. If graphs or figures are utilized, be sure
to include a written description of the information they contain.
-
Please try to be complete and concise. This can be a difficult balance
to achieve, but is essential for effective technical writing.
-
Some parts of the project will be most easily solved by hand, others
using the computer. Feel free to use any software (Maple, QuattroPro,
WordPerfect, MathCAD, etc.) that you find useful.
-
Start early. Divide the project into separate parts. Work on one part at
a time. And, if (and when) you have any questions, please do not hesitate
to ask me for guidance.
-
Do not put this off until the last few days. You should start your
work before Spring Break. Waiting until after Spring Break will
most likely lead to an unnecessary (and unhealthy) last-minute rush
to complete the report.
-
The final project report is due in my office by 5:00P.M. on Friday,
March 24, 1995.
Part 3 -- Analyze Your Own Project
-
Now that you have analyzed one project and gained some experience working
together as a group, I want you to investigate one of the projects turned
in as Part I of this project. Each group will select a different project.
-
Your first step should be the selection of the project to be studied.
You may need to revise the project description so that it is more focused.
(Be sure you can identify specific questions that you need to be answered.)
I will be glad to consult with you on these revisions, but all final
decisions are yours.
-
You are encouraged to obtain my approval of the project you select. This
decision should be made before April 1.
-
The remainder of this portion of the project should be similar to Part II,
with the obvious exception that each group's problem will be different.
Use my feedback on your earlier reports to improve the quality of this
final report.
-
The group project report, which should include a copy of the (revised)
project description, is due in my office by 5:00P.M. on Friday,
April 14, 1995.
-
In addition to the project report, each team member should prepare a
short (more than one sentence, less than a page) individual summary of
the group experience. Some issues you might choose to address include:
- How well did your group coordinate their efforts?
- Did all members share equally in the workload?
- What obstacles did you encounter?
- What were some good parts of the experience?
This is worth five (5) points. I will be looking for correct grammar
and spelling as well as the use of complete and well-organized sentences.
These summaries are due in class on Wednesday, April 19, 1995.
One-Page Project Outline
TITLE: Consecutive Reactions in Batch Reactors
NAME: Doug Meade
FACULTY CONTACT: Prof. Ralph White, Chemical Engineering (ECHE 430)
PHYSICAL DESCRIPTION:
Consider a reaction involving three substances, A, R, and S, which
have first-order reaction rates and are carried out isothermically in
either the gas or liquid phase in a perfectly mixed batch reactor. The
reaction begins with a pure sample of component A.
Schematically, the process can be represented as:
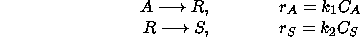
where 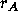 is the reaction rate for the conversion of A into R,
is the reaction rate for the conversion of A into R,
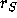 is the rate at which R is converted into S;
is the rate at which R is converted into S; 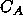 and
and 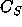 are the concentrations of A and S, respectively.
are the concentrations of A and S, respectively.
The primary objective is to determine the amount of each substance in
the reactor up to time after the reaction starts. Additional information
that is desired includes the time at which the amount of substance R is
a maximum, the time at which the amount of S exceeds the amount of A,
and the total amount of substance S produced at any time t>0.
MATHEMATICAL FORMULATION:
This is really just a three-compartment container problem. Looking at the
inflow and outflow for each substance leads to a system of three first-order
differential equations with initial conditions.
Let 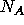 ,
, 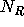 , and
, and 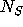 denote the number of moles of A, R, and S
at any time in the reactor. The volume of solution in the tank is assumed to
be constant. Then, conservation of the total amount of each of the three
components can be expressed as
denote the number of moles of A, R, and S
at any time in the reactor. The volume of solution in the tank is assumed to
be constant. Then, conservation of the total amount of each of the three
components can be expressed as
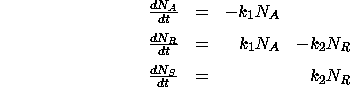
with initial conditions 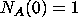 ,
, 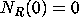 ,
, 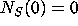 .
This system can be solved using the ideas for first-order linear ODEs.
.
This system can be solved using the ideas for first-order linear ODEs.
Once the solution is obtained, answers to the specific questions can be
obtained as follows:
-
the maximum amount of component R occurs at a time when
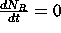
-
the solutions to
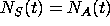 will be used to determine when the amounts
of S and A are equal (this is used to determine when the amount of S
exceeds the amount of A).
will be used to determine when the amounts
of S and A are equal (this is used to determine when the amount of S
exceeds the amount of A).
-
the total amount of S produced up to time T is given by the integral
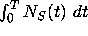 .
.
A graph will be used to show the number of moles of each component as a
function of time.
DATA:
Two different set of parameter values are 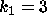 ,
, 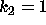 and
and 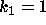 ,
,
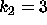 . With these parameters it will be possible to see some of the
differences that arise between the cases
. With these parameters it will be possible to see some of the
differences that arise between the cases  and
and  . Using
. Using
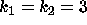 will be useful in investigating any differences that occur
when
will be useful in investigating any differences that occur
when 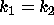 .
.
REFERENCES:
C. D. Holland and R. G. Anthony, Fundamentals of
Chemical Reaction Engineering, Prentice--Hall, 1979.
Douglas B. Meade
Last revision: Wed Feb 8 14:04:33 EST 1995


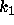 and
and 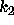 until you need to produce a plot. (If you analysis does
not apply for certain combinations of the parameters, be sure to mention
this.)
until you need to produce a plot. (If you analysis does
not apply for certain combinations of the parameters, be sure to mention
this.)
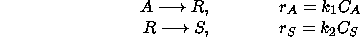
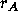 is the reaction rate for the conversion of A into R,
is the reaction rate for the conversion of A into R,
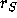 is the rate at which R is converted into S;
is the rate at which R is converted into S; 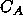 and
and 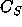 are the concentrations of A and S, respectively.
are the concentrations of A and S, respectively.
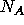 ,
, 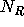 , and
, and 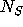 denote the number of moles of A, R, and S
at any time in the reactor. The volume of solution in the tank is assumed to
be constant. Then, conservation of the total amount of each of the three
components can be expressed as
denote the number of moles of A, R, and S
at any time in the reactor. The volume of solution in the tank is assumed to
be constant. Then, conservation of the total amount of each of the three
components can be expressed as
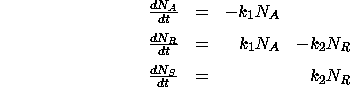
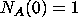 ,
, 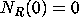 ,
, 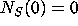 .
This system can be solved using the ideas for first-order linear ODEs.
.
This system can be solved using the ideas for first-order linear ODEs.
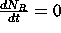
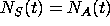 will be used to determine when the amounts
of S and A are equal (this is used to determine when the amount of S
exceeds the amount of A).
will be used to determine when the amounts
of S and A are equal (this is used to determine when the amount of S
exceeds the amount of A).
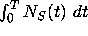 .
.
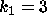 ,
, 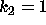 and
and 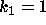 ,
,
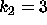 . With these parameters it will be possible to see some of the
differences that arise between the cases
. With these parameters it will be possible to see some of the
differences that arise between the cases  and
and  . Using
. Using
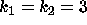 will be useful in investigating any differences that occur
when
will be useful in investigating any differences that occur
when 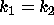 .
.