Lab Overview
A common theme in this course, and the labs, has been the construction of new functions from known functions. This theme can be extended to the construction of Taylor series expansions for functions based on known Taylor series expansions. The power of this method is that you only need to remember a small number of fundamental power series:
geometric series
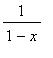 =
=
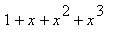 + ...
+ ...
=
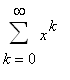 -1 <
-1 <
 < 1
< 1
exponential
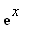 =
=
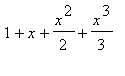 + ...
+ ...
=
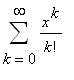
binomial
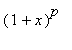 = 1 +
= 1 +
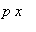 +
+
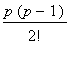
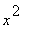 +
+
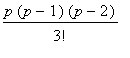
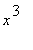 + ...
+ ...
=
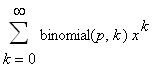 -1 <
-1 <
 < 1
< 1
where
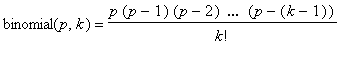 .
.
The example repeats the derivation of the Taylor series for
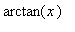 presented in class. You will then apply similar techniques to determine power series expansions for other functions. The Lab Questions are very similar to the example, and to exercises in the text.
presented in class. You will then apply similar techniques to determine power series expansions for other functions. The Lab Questions are very similar to the example, and to exercises in the text.
A new feature of this - and all remaining labs this semester - is an integration problem. Each of these problems will be worth at least 2 bonus points towards your lab grade. Note that your answer must contain the correct evaluation of the integral and an explanation of the method(s) used to evaluate the integral. (An example is provided later in this worksheet.) You are encouraged to use the
Integration
maplet [
Maplet Viewer][
MapleNet] to help with this problem.
Deadline for submitting a lab solution is midnight, Thursday, April 3, 2003.
Example 1: The Power Series for
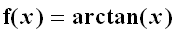
Define

The key observations are that the derivative of the arctangent function is a rational function
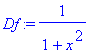
This provides a definition of the arctangent function as an integral:
| > |
F := Int( 1/(1+t^2), t=0..x );
|
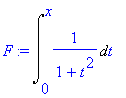
To verify that this is correct,
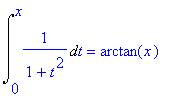
Next, recognize the integrand in this definition as the sum of the geometric series with base
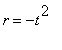 . That is, if the geometric series with base
. That is, if the geometric series with base
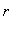 is
is
| > |
GS( r ) = value( GS(r) );
|
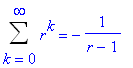
Then, the Maclaurin series for
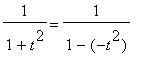 is
is
| > |
Df_series := GS( -t^2 );
|
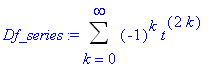
To verify this, observe that Maple reports
| > |
Df_series = value(Df_series);
|
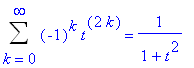
The power series for the arctangent function is obtained by term-by-term integration of the terms of the above series.
| > |
f_series := Int( Df_series, t=0..x );
|
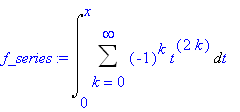
It is difficult to get Maple to interchange the integral and the sum and evaluate only the integrals in the above formula. It is much simpler to work with the truncated series with a finite number of terms. For example, the first 10 terms of the power series for
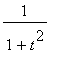 are
are
| > |
Df_10 := value( GS( -t^2, 10 ) );
|
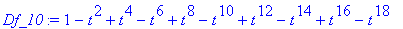
The integration of this polynomial gives the first 10 non-zero terms in the power series for arctangent:
| > |
F_10 := Int( Df_10, t=0..x );
|
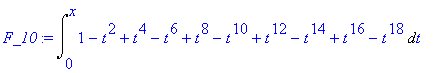
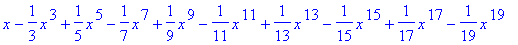
To confirm this, note that Maple computes the first 10 non-zero terms of the Maclaurin series for the arctangent function to be:
| > |
series( arctan(x), x=0, 20 );
|
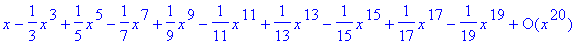
The general form of this power series can be deduced from the above result or by manual integration of the general term in the formula obtained previously:
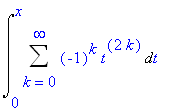
| > |
f_termK := Int( (-1)^k*t^(2*k), t=0..x ):
f_termK2 := value(f_termK) assuming k::posint:
f_termK = f_termK2;
|
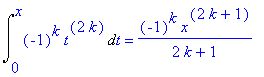
| > |
f_series2 := Sum( f_termK2, k=0..infinity );
|
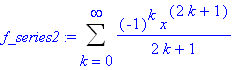
To verify this formula, note that the first 10 nonzero terms of this series are
| > |
series(value(%),x=0,20);
|
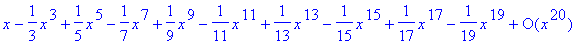
These are in complete agreement with the result found earlier.
To address the radius of convergence for the power series for
 , begin with the fact that the geometric series converges for -1 <
, begin with the fact that the geometric series converges for -1 <
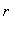 < 1. With
< 1. With
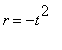 , this yields:
, this yields:
-1 <
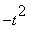 < 1
< 1
-1 <
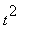 < 1
< 1
-1 <=
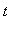 < 1
< 1
Term-by-term integration preserves this radius of convergence:
-1 <=
 < 1
< 1
All that remains is to check the endpoints
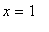 and
and
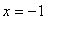 . For
. For
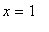 :
:
| > |
eval( f_series2, x=1 );
|
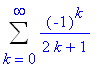
Note that the terms of this series alternate sign and
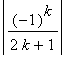 is a decreasing sequence as
is a decreasing sequence as
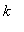 ->
->
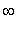 . Thus, the Alternating Series Test states that this series converges.
. Thus, the Alternating Series Test states that this series converges.
For
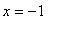 :
:
| > |
simplify(eval( f_series2, x=-1 ));
|
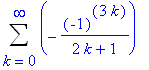
the series is the negative of the series for
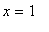 and so is convergent. Thus, the interval of convergence for the power series for the arctangent function is [-1,1].
and so is convergent. Thus, the interval of convergence for the power series for the arctangent function is [-1,1].
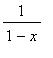 =
=
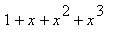 + ...
+ ... 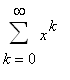 -1 <
-1 <
![]() < 1
< 1
![]() =
=
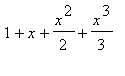 + ...
+ ...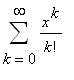
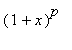 = 1 +
= 1 +
![]() +
+
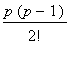
![]() +
+
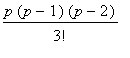
![]() + ...
+ ...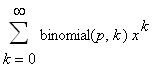 -1 <
-1 <
![]() < 1
< 1
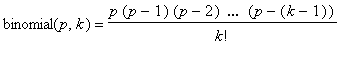 .
.
![]() presented in class. You will then apply similar techniques to determine power series expansions for other functions. The Lab Questions are very similar to the example, and to exercises in the text.
presented in class. You will then apply similar techniques to determine power series expansions for other functions. The Lab Questions are very similar to the example, and to exercises in the text.
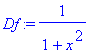
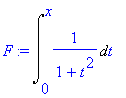
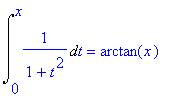
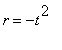 . That is, if the geometric series with base
. That is, if the geometric series with base
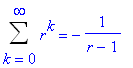
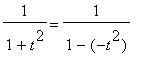 is
is
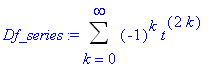
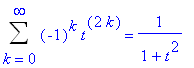
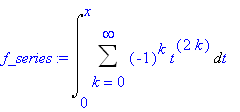
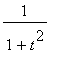 are
are
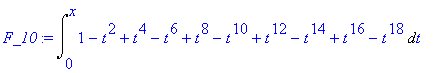
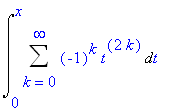
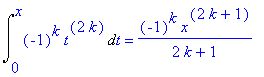
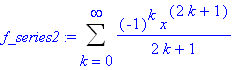
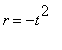 , this yields:
, this yields:
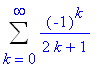
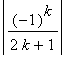 is a decreasing sequence as
is a decreasing sequence as
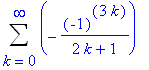
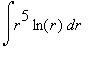 .
.
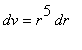 (so
(so
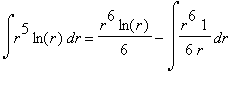
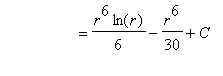 .
.
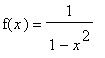 =
=
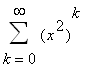 for -1 <
for -1 <
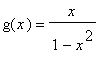 .
.
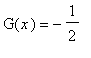
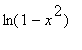 . If you cannot find the general term in the series, find the first 10 non-zero terms in the power series.
. If you cannot find the general term in the series, find the first 10 non-zero terms in the power series.
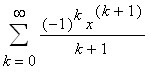 for -1 <
for -1 <
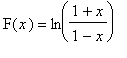 .
. 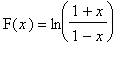 .
.
 . Be sure to explain the major steps leading to your answer (as in Example 2).
. Be sure to explain the major steps leading to your answer (as in Example 2).