The Pythagorean Theorem and The Area of A Triangle

The Pythagorean Theorem. If the legs of a right triangle have length A and B, then the length of the hypotenuse is C where C² = A² + B².

The Sumerians are known to have discovered and applied the Pythagorean Theorem around 2500 B.C. – more than 4000 years ago! It was not until around 400 B.C. that Pythagoras found a proof that this statement is true for any right triangle.

A proof is a logical explanation that makes use of accepted facts to determine the truth of the statement. In many ways, a proof is like a definition of a vocabulary word. A mathematician never accepts a (mathematical) statement until it can be proven.

To understand why it is important to have a proof, consider the statement: The value of n²-n+11 is a prime number for all positive integers n. If the first ten positive integers are tested, the results are all primes:

n	n^2-n+11
1	11
2	13
3	17
4	23
5	31
6	41
7	53
8	67
9	83
10	101

But, for n=11, the value is 11²-11+11 = 11² which is not a prime number. Therefore, the statement about n²-n+11 being prime for all positive integers is false.

There are many proofs of the Pythagorean Theorem. The proof that we will discuss can be explained with a couple simple diagrams involving squares, rectangles, and triangles.

Proof of The Pythagorean Theorem: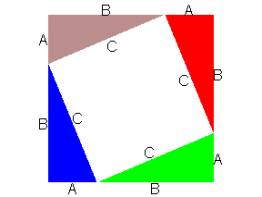

Form a square with side length equal to the sum of the lengths of the two legs of the right triangle: A+B. In each corner, construct the right triangle with hypotenuse C. Note that the region in the center is a square with sides of length C. (See the figure on the right.) The total area of square with sides A+B is the area of the four right triangles + area of the square with sides C.

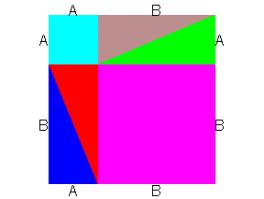
In the figure on the right the four triangles have been relocated. Note that the total area of the square with sides A+B is the area of the same four right triangles + area of the square with sides A + area of the square with sides B. Because the areas of the square with sides A+B has not changed, it is seen that the area of the square with sides C = area of the square with sides A + area of the square with sides B. That is, C² = A²+B². This completes the proof of the Pythagorean Theorem.

Area of a Triangle. The area of a triangle is one-half the product of the base and height of the triangle.

The proof of this statement can be provided using the ideas developed on the supplemental pages. This proof is slightly different for right, acute, and obtuse triangles. But, since every triangle is either right, acute, or obtuse, this argument does verify the truth of this statement for every possible triangle.

To test your understanding of this statement, find the area of the triangle in the figure below.

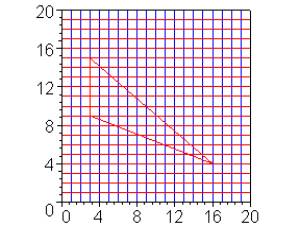
Hint: Use the Pythagorean Theorem.

References:

1. Ask Dr. Math, The Math Forum, WWW: http://mathforum.com/dr.math/faq/faq.pythagorean.html

2. The Proof, NOVA, PBS, WWW: http://www.pbs.org/wgbh/nova/proof/puzzle/

3. Area of A Triangle, The Math League: WWW: http://www.mathleague.com/help/geometry/area.htm

Prepared by Dr. Douglas B. Meade for Mrs. Steisslinger’s Fifth Grade Class at Bookman Road Elementary School. Please direct questions and comments to Dr. Meade at meade@math.sc.edu.