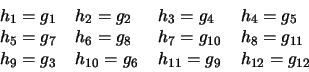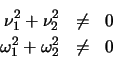Next: Código
Up: Sobre demostración automática de
Previous: Introducción
Supongamos que los puntos A y B tienen por coordenadas A=(0,1) y
B=(0,-1), siendo las coordenadas de los centros de las circunferencias
C1=(a,0). y
C2=(b,0) Consideremos vectores
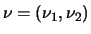 y
y
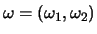 con puntos de anclaje en Ay B respectivamente. Una recta por A y vector director
con puntos de anclaje en Ay B respectivamente. Una recta por A y vector director 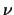 corta a la
circunferencia C1 en el punto
A1=(x1,y1). Para calcular sus
coordenadas hemos de considerar al punto A1 como perteneciente a la
recta anterior: Así,
corta a la
circunferencia C1 en el punto
A1=(x1,y1). Para calcular sus
coordenadas hemos de considerar al punto A1 como perteneciente a la
recta anterior: Así,
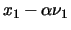 |
= |
0 |
(1) |
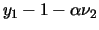 |
= |
0 |
(2) |
La condición de pertenecer igualmente a la circunferencia C1 viene
dada por la siguiente ecuación de segundo grado en x1 e y1:
Al substituir con las igualdades anteriores en esta, obtenemos la siguiente
ecuación de segundo grado en 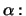
Una de sus soluciones es obviamente
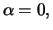 lo que nos ofrece el punto A. La otra solución de
lo que nos ofrece el punto A. La otra solución de 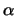 será la que nos interesará
1:
será la que nos interesará
1:
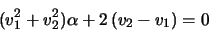 |
(3) |
Sean
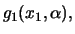
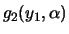 y
y
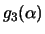 los
polinomios que conseguimos con las ecuaciones (1), (2) y (3) respectivamente. Usando el mismo procedimiento conseguimos
polinomios
los
polinomios que conseguimos con las ecuaciones (1), (2) y (3) respectivamente. Usando el mismo procedimiento conseguimos
polinomios
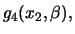
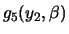 y
y
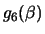 (al
considerar el punto A2),
(al
considerar el punto A2),
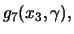
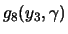 y
y
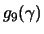 (al considerar el punto B1) y finalmente
(al considerar el punto B1) y finalmente
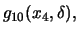
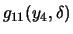 y
y
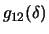 (al
considerar el punto B2). El ponimonio tesis se consigue al considerar
la ecuación que establece el paralelismo de los segmentos
A1B1 y
A2B2.
(al
considerar el punto B2). El ponimonio tesis se consigue al considerar
la ecuación que establece el paralelismo de los segmentos
A1B1 y
A2B2.
(y4-y2)(x3-x1)-(y3-y1)(x4-x2)=0
Usando ahora el método de Ritt-Wu con estos polinomios (obsérvese
que no es necesario triangular previamente el sistema, pues simplemente
ordenando los polinomios convenientemente se tiene conseguido este
propósito), obtenemos la demostración de la afirmación pedida.
Observamos que las condiciones de degeneración se reducen a que los
vectores 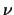 y
y 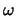 sean no nulos:
sean no nulos:



Next: Código
Up: Sobre demostración automática de
Previous: Introducción
Francisco Blanco-Silva
2001-01-11
![]() y
y
![]() con puntos de anclaje en Ay B respectivamente. Una recta por A y vector director
con puntos de anclaje en Ay B respectivamente. Una recta por A y vector director ![]() corta a la
circunferencia C1 en el punto
A1=(x1,y1). Para calcular sus
coordenadas hemos de considerar al punto A1 como perteneciente a la
recta anterior: Así,
corta a la
circunferencia C1 en el punto
A1=(x1,y1). Para calcular sus
coordenadas hemos de considerar al punto A1 como perteneciente a la
recta anterior: Así,