TASK: Use bisection to solve for the value of the golden ratio, phi.
COMMENT: One definition of the golden ratio phi is as follows:
phi = 1 + 1/phi
Think about this fact. Suppose you didn't know the value of phi, but just this fact. How can you use bisection to find the value?
It might help your thinking to rewrite the equation using "x" instead:
x = 1 + 1/x.
Now come up with a function f(x) which will be zero if the equation is true.
This is the function we can use bisection on.
INSTRUCTIONS:
You will need the function "bisection3.m", copied from the homework directory.
Write a function golden.m that evaluates the function whose zero
we are seeking.
Make an initial plot of "golden" over the interval [0,3].
Use bisection to estimate the value of the solution.
Print:
* your value x,
* the exact value of phi = (1+sqrt(5))/2
* the error abs(x-phi).
CHECK: Your error should be no bigger than the xtol value you pick. A plot of the results could be made with commands like
plot ( xlist, ylist, ...
xlist, 0*ylist, 'k:', ...
x, 0, 'r.', ...
'Linewidth', 3, 'Markersize', 50 );
and the result should be something like hw043.jpg: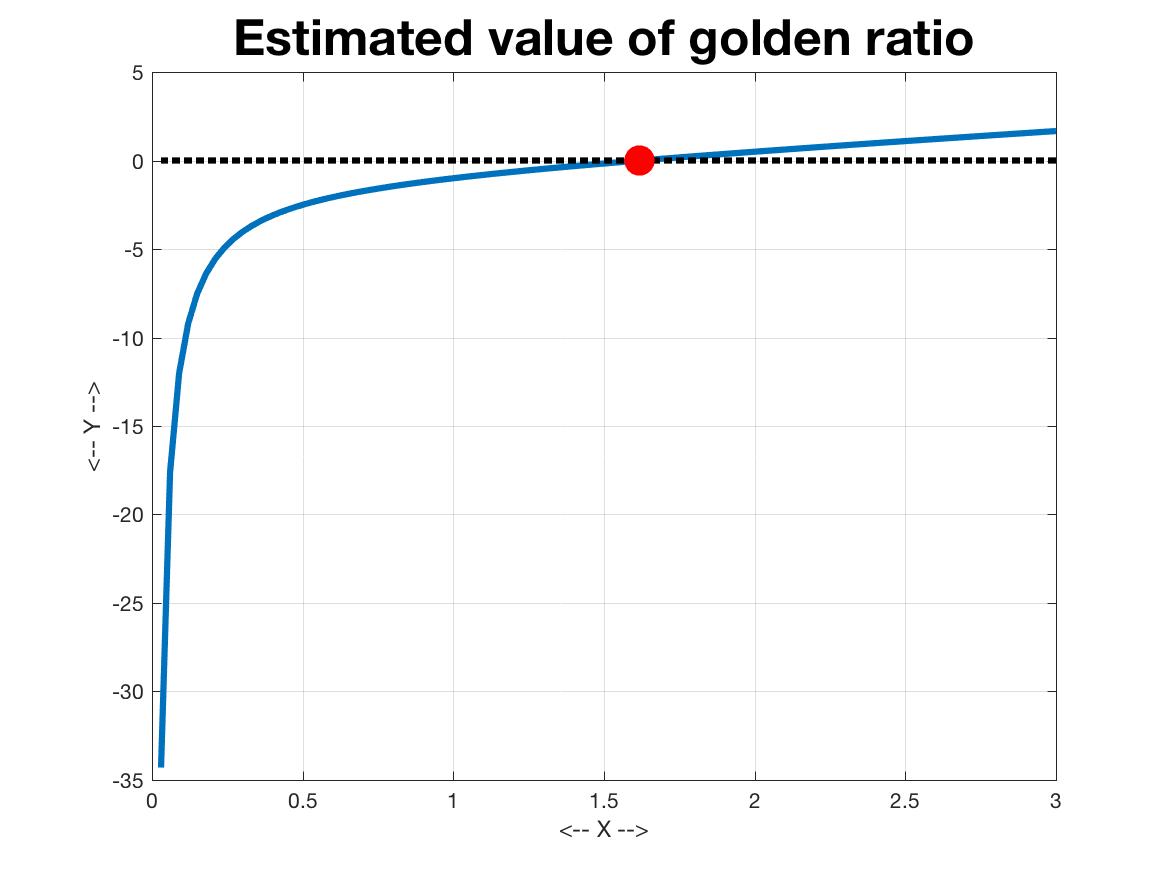
SUBMIT: Your script file should be named "hw043.m", and begin with:
% hw043.m
% YOUR NAME
% This script (describe what it does)