TASK: Use bisection to find three zeros of a cubic function.
COMMENT: The function y(x)=816x^3 - 3835x^2 + 6000x - 3125 is a cubic polynomial. There are three values x for which y(x)=0. We want to find approximate values of these three zeros.
When a function has several zeros to find, we need to break up the region into separate change-of-sign intervals. One way to do this is to start with a plot of the function f(x), get rough locations of the zeros, (say x1, x2, and x3), and then find four values that separate them:
v1 < x1 < v2 < x2 < v3 < x3 < v4
Notice that the values of cubic(v1), cubic(v2), cubic(v3) and cubic(v4)
should alternate it sign, that is, + - + - or else - + - +.
Once you have the values v1, v2, v3, and v4 you can use bisection in
[a=v1,b=v2] to find x1;
[a=v2,b=v3] to find x2;
[a=v3,b=v4] to find x3.
INSTRUCTIONS:
You will need the function "bisection3.m", copied from the homework directory.
Write a function cubic.m that evaluates the function whose zeros
we are seeking.
Make an initial plot of "cubic" over the interval [0,3].
This range will be too big to see the details, so reduce the range
a few times until you can clearly see the graph of the function
cross the x axis three times. Choose values v1, v2, v3 and v4
that separate these three locations.
Now write a script that uses bisection 3 times, to compute estimates
for the zeros x1, x2, and x3.
Print your values x1, x2, and x3.
CHECK: You should expect that x1, x2 and x3 are distinct values, and that the cubic function is approximately zero for each of these inputs. A plot of the results could be made with commands like
plot ( xlist, ylist, ...
xlist, 0*ylist, 'k:', ...
x1, 0, 'r.', ...
x2, 0, 'r.', ...
x3, 0, 'r.', ...
'Linewidth', 3, 'Markersize', 50 );
and the result should be something like hw042_noaxis.jpg: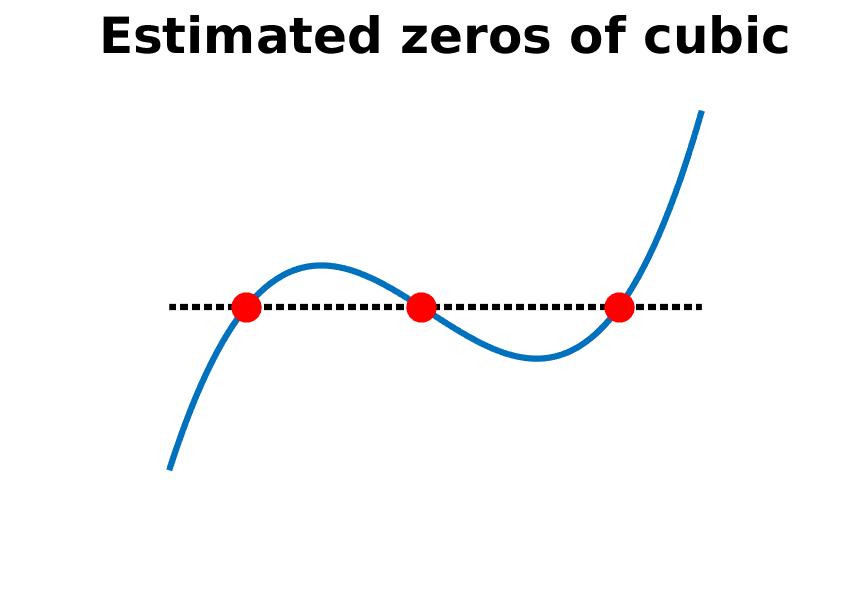
SUBMIT: Your script file should be named "hw042.m", and begin with:
% hw042.m
% YOUR NAME
% This script (describe what it does)