TASK: Use bisection to find a zero of the function f(x)=x^3-2x-5.
COMMENT: Although this function is a cubic polynomial, which could have three solutions to the problem, it will actually only have one (real) solution.
INSTRUCTIONS:
Copy the function "bisection3.m" from the homework directory.
Write a function wallis.m that evaluates the function whose zero
we are seeking.
Write a script which calls bisection3 to seek a zero of the
wallis function. Your search should begin in the interval [0,3].
Then print
* the solution x,
* the value of wallis(x),
* the width of the interval (b-a) (this should be small now!)
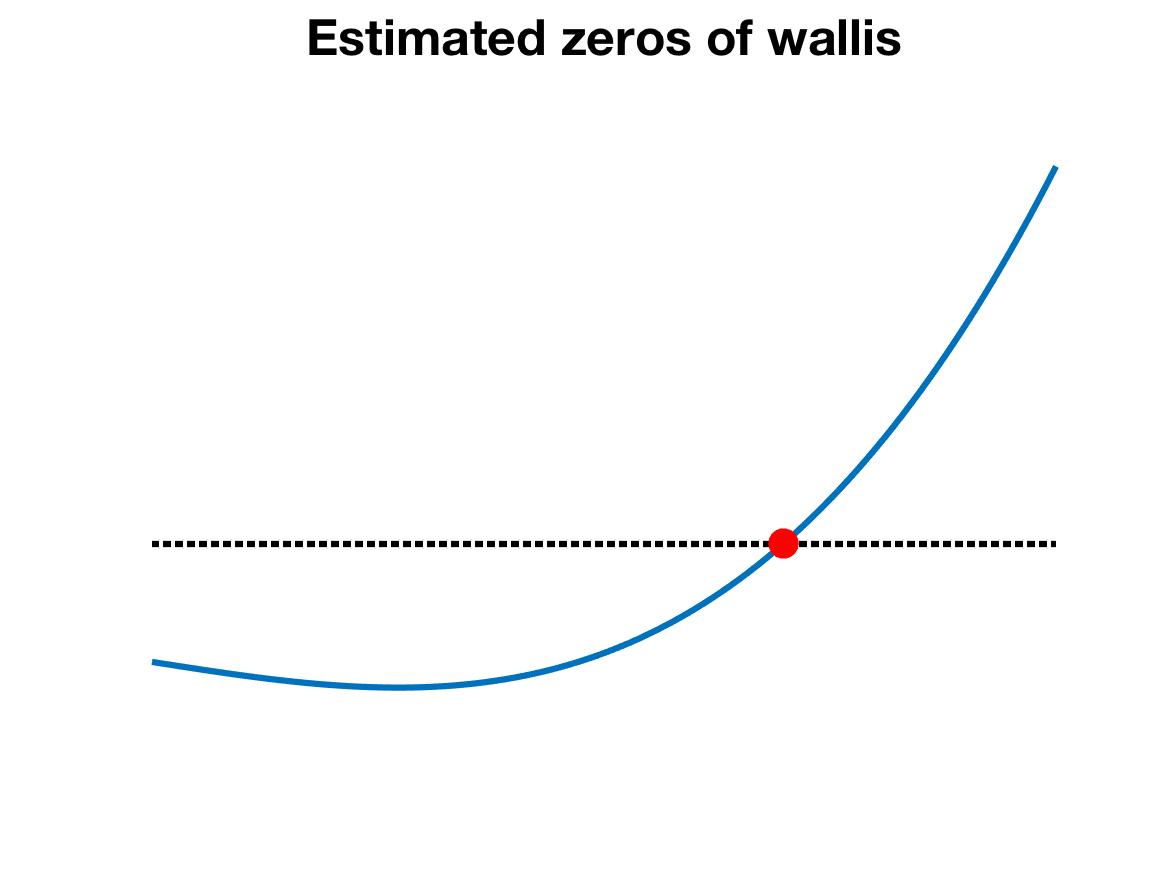
display the function and your estimated solution:
xlist = 101 points in [0,3]
ylist = wallis ( xlist );
plot ( xlist, ylist,
xlist, 0*ylist, 'k:',
x, 0, 'r.',
'Linewidth', 3, 'Markersize', 50 );
CHECK:
Your plot should be something like hw041_noaxis.jpg:

SUBMIT: Your file should be named "hw041.m", and begin with:
% hw041.m
% YOUR NAME
% This script (describe what it does)